点积和叉乘的区别
2018-01-17 创建人:Ruo_Xiao
邮箱:xclsoftware@163.com
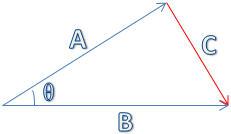
假设:

一、点积(内积)
1、A和B的点积公式:
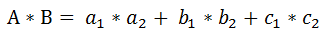
其结果是标量。
2、几何意义:A乘以B在A上的投影。
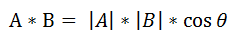
推导过程如下:
根据三角形余弦定理:
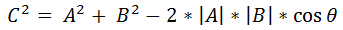
而C = A - B,则:
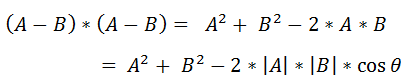
所以:
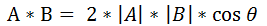
二、叉乘(外积、叉积、向量积)
假设:
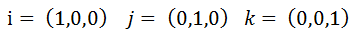
1、人为定义的运算,需要满足如下条件:
(1)|C| = |A||B|sinθ。
(2)C的方向遵循右手螺旋定则。
(3)C垂直A和B确定的平面,计算结果是向量。
(上述据说是高等数学里面的东西,后续再查)
拓展:右手螺旋定则
右手四指由矢量A的方向,并沿小于180°角向矢量B的方向弯曲(环绕),则伸直的大拇指所指的方向就是矢量C的方向。
由(1)可知:
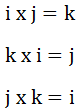
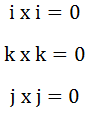
2、公式推导
(1)
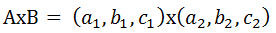
(2)
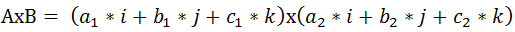
(3)展开:
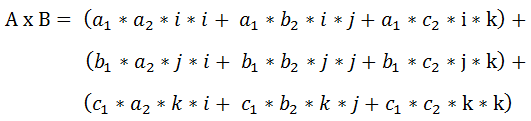
(4)进一步计算,得:
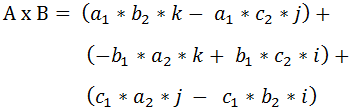
(5)最后合并,得:
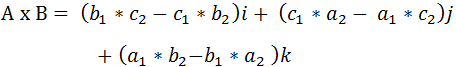
(6)结论:
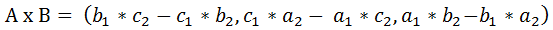
(7)简易理解方法:
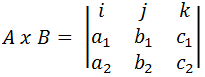
3、几何意义
叉乘结果的模长|C|正好是A向量和B向量组成的平行四边形的面积。(巧合)
(SAW:Game Over!)
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!