【论文笔记】AP聚类算法解读

文章目录

• • 引子
  • 自己体会
  • • 吸引信息更新公式
    • 归属信息更新公式
    • 松弛因子引入
  • 缺点评估

引子

网络上已经有很多关于AP算法的介绍了，托他们的福，我更快地理解了AP算法。但是感觉他们不说人话，只说了很抽象的概念，公式理解起来还是有点费工夫。所以我就自己写写自己的体会。

这里列两篇我看过的博客，重复内容比如AP的基本概念、优势什么的我就不列了。

AP算法解析
AP-python代码

说实话，AP算法是一个很优秀的算法，但是它却因为理解成本比KMeans、KNN高得多而很少被编入教材中，所以这个算法鲜有人知道。

自己体会

首先AP属于聚类算法，个人对它的定位属于K-means的上位替代，尤其是在分组个数不给定的情况下。

AP算法的核心就是吸引度矩阵R和归属度矩阵A。当然衡量两点距离的S也很重要，不过S一开始就给定了。关于s，值得注意的一点就是s(i,k)<0,且越相似的两点S越大（越接近0）。

接下来仔细说说那些个核心公式：

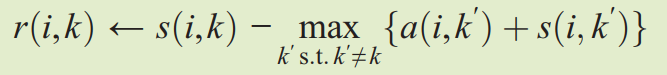
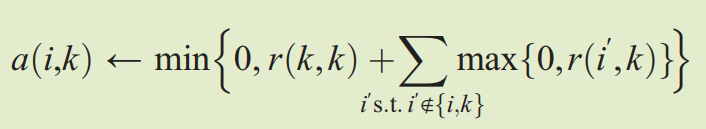
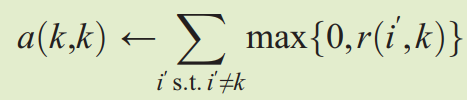
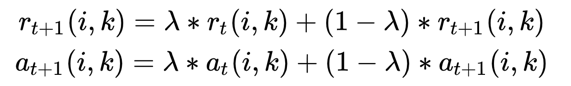
这几个公式散落在文章的各个角落，但是是AP聚类算法中主循环就是上面这些公式。

吸引信息更新公式

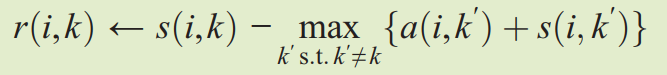
r(𝑖,𝑘)描述了数据对象𝑘适合作为数据对象𝑖的聚类中心的程度，表示的是从𝑖到𝑘的消息。

说人话就是 i被k吸引的程度=i到k的距离-其它点吸引i的程度的程度
反映出来的是：一个点越是被很多点吸引，就越是不容易被特定的点吸引。
当然这里论文里取的是"最吸引i"的那个点对i的吸引程度作为i受欢迎程度的度量。

归属信息更新公式

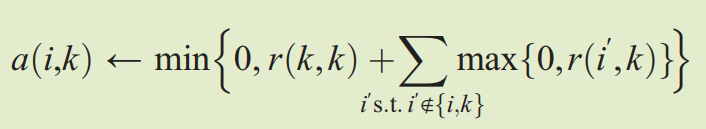
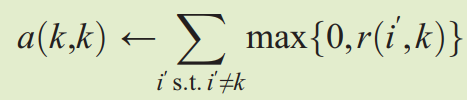
𝑎(𝑖,𝑘)描述了数据对象𝑖选择数据对象𝑘作为其聚类中心的适合程度，表示从𝑘到𝑖的消息。

说人话就是 i对k的归属程度 = i被k的吸引程度+k对其它点的吸引程度
等式右边第一项直观上很好理解，越被吸引就越容易归属。
等式右边第二项其实就是衡量以k为中心的这个簇的大小，这个簇越大，那么i就越容易“随大流”，归属于一个大家族。

松弛因子引入

防止震荡不收敛，文章中采用的松弛系数为 0.5。

缺点评估

大伙都在说AP的优点，我来说几个缺点。

• 虽然AP算法不用提前设置聚类中心的个数，但是需要事先设置参考度(preference value)，即s(k, k)的值，其大小与聚类中心的个数正相关。
• 由于AP算法每次迭代都需要更新每个数据点的吸引度值和归属度值，算法复杂度较高，在大数据量下运行时间较长。AP算法的时间复杂度较高，一次迭代大概O(N³)。相比kmeans的O (TKN)，显然是AP算法更耗时。
• AP算法需要事先计算每对数据对象之间的相似度，内存可能会放不下。
• 聚类的好坏受到参考度和阻尼系数的影响。（新的超参）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！