频谱分析基础-02.频谱相位及栅栏效应的引出

目录

1.背景

2.程序及原理分析

3.幅度和相位谱及栅栏效应

4.问题

1.背景

关于频谱分析主要研究对应频率信号的幅度和相位，因此对信号进行FFT变换后，需要求分别画出其幅度谱和相位谱。同时我们验证一个理论：实信号的频谱是共轭对称的。同时上节提出：关于采样频率fs和采样深度如何选择？这个问题，看看会出现哪些不可思的现象。

2.程序及原理分析

clear all; clc; close all;

fs= 1000;

N=1000;

t=(0:N-1)/fs;

f1=50;f2=65.75;

x=cos(2*pi*f1*t+pi/4)+cos(2*pi*f2*t);

X=fft(x,N)/N;

Y=fftshift(X);

freq1=(-N/2:N/2-1)*fs/N;

Y1=abs(Y);

Theta=angle(Y);

%作图

subplot 211;

stem(freq1,Y1,'k');xlim([-150 150]);

xlabel('频率（Hz）');ylabel('幅值');

set(gcf,'color','w');

subplot 212;

stem(freq1,Theta,'k');xlim([-150 150]);

xlabel('频率（Hz）');ylabel('相位');

set(gcf,'color','w');

3.幅度和相位谱及栅栏效应

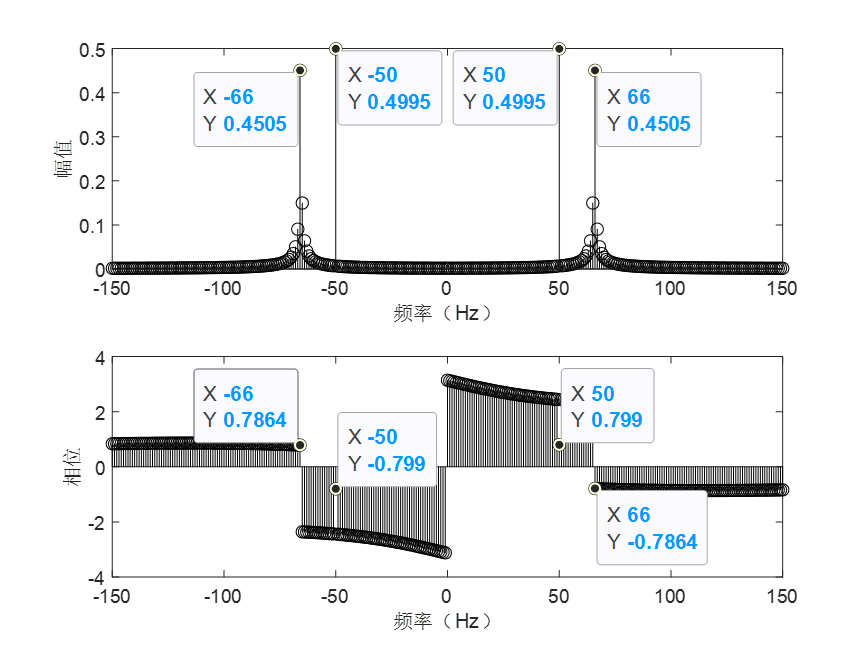
图 1 幅度谱和相位谱

对于信号x=cos(2*pi*50*t+pi/4)+cos(2*pi*65.75*t)，包括两个单音信号分别为f1 频率为50Hz,初始相位为pi/4。 f2  频率65.75Hz,初始相位为0；对于频率f1的信号幅度都为0.5，相位为0.799（pi/4），呈现出共轭对称；对于频率f1的信号，我们发现频谱图上不存在准确的62.75Hz的信号，而是在其附近鼓起来很多信号，似乎距离越近幅度也越大，其实这也符合能量守恒定理。。最近的信号是66Hz,幅度都为0.4505，相位为-0.7864，虽然也呈现出共轭对称，但是明显小于理想的0.5，相位更不是理想的0。这就是比较典型的栅栏效应。

4.问题

  问题：如何消除栅栏效应？对于信号的频率与FFT后的谱线不重合如何求解幅度和相位谱？

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！