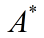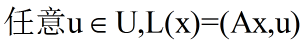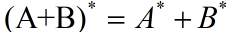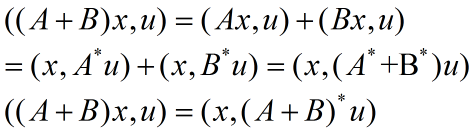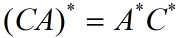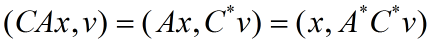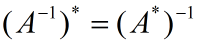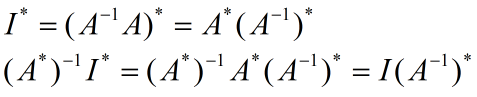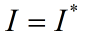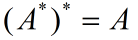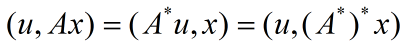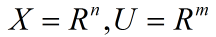线性代数(四十一) : 伴随矩阵
本节介绍伴随矩阵的概念,伴随矩阵可用于解超定方程
1 伴随
设X和U是两个欧几里得空间,若A是X到U的线性映射,则A的转置将U映射到X,
为了和一般意义的转置加以区别,我们将欧几里得空间X到U的线性映射A的转置称为
A的伴随,记做:
完整定义如下:
也可以写为:
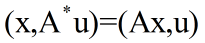
上式左端表示空间X中的标量积,右端表示U中的标量积
2 伴随的性质
(i) 若A,B均是X到U的线性映射,则:
证明:
由于标量积是线性函数,再根据(1)式有:
(ii)若A为X到U的线性映射,C为U到V的线性映射,则:
证明:
(iii)若A为X到U的一一映射(既是单射也是满射,也就是可逆映射),则:
证明:
根据性质(ii):
又因为I是恒同映射:
得证.
(iv)
证明:
根据标量积的对称性重写(1)式:
3 伴随矩阵
若令:
其中的结构是欧几里得结构,将A和A*看做矩阵,则他们互为对方的伴随矩阵(也可说转置)
下节将介绍伴随矩阵的一个重要应用.
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!