矩阵的运算以及含意
1 矩阵的乘法在函数中的表达方式就是映射
不同的函数对应不同的坐标系,A•B就是矩阵A投影到矩阵B中,相应的向量坐标也会在投影后重新分部。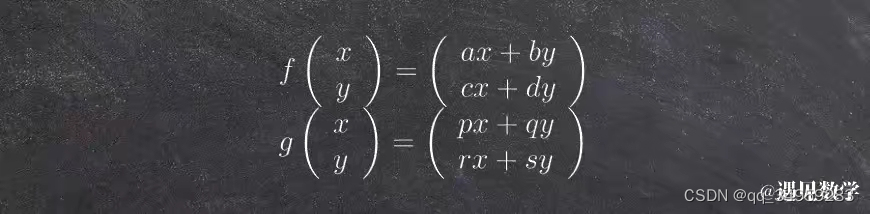
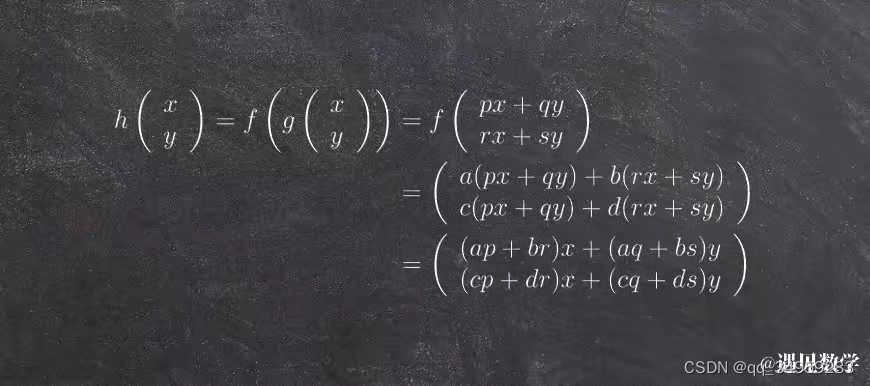
2 矩阵的叉乘就是取矩阵的行列式
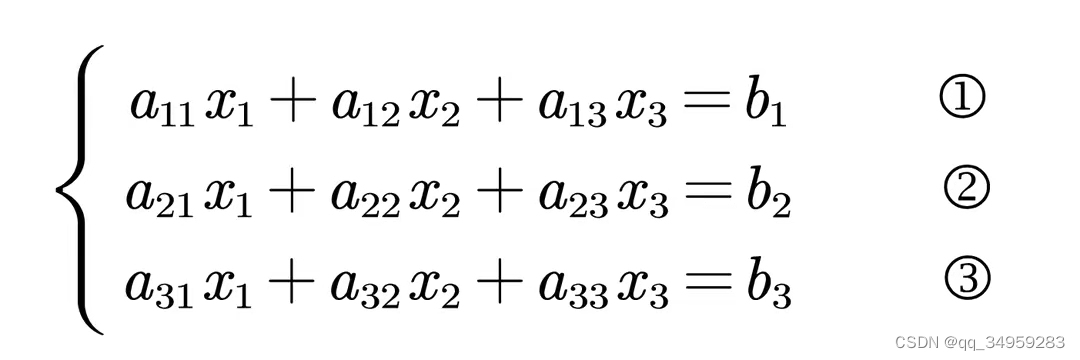

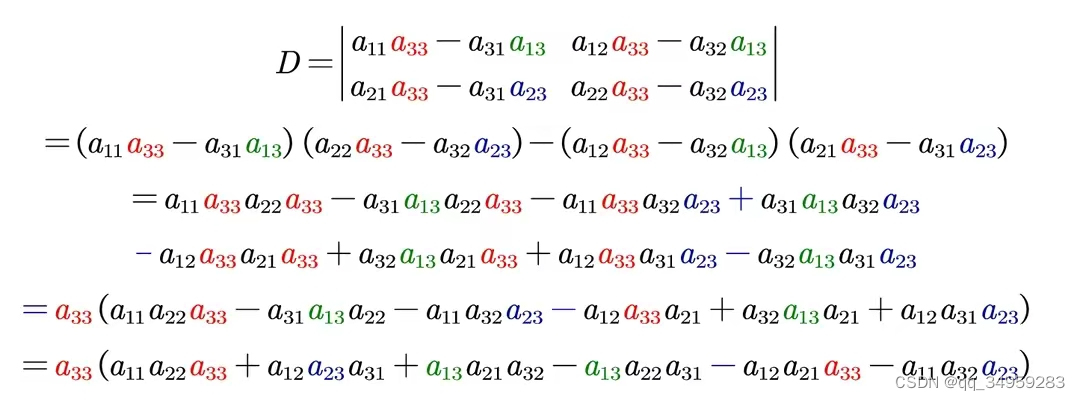

行列式是由线性方程推导来的,在矩阵几何中是向量组成的平行四边形面积(二维)或则平行六面体体积(三维)。
3 矩阵的点乘

利用一个向量到另一个向量的投影与被投影向量的模的积两两相同证的向量点积公式。
4 矩阵的特征值

5 矩阵的旋转矩阵

三维同理可推导。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!