python实现最小二乘法求解线性回归问题

本次实验样本集（x）及标签列表如下：

'''
para X:矩阵，样本特征矩阵
Para Y:矩阵，标签向量
return：矩阵，回归系数
'''
times = [30,45,60,75,90,105] #测量时间列表（样本）
gravity = [150,141,130,119,108,100]#重力数据列表（标签）
import numpy as np
def least_square(X,Y): #定义最小二乘拟合函数W=(X*X.T).I*X*Y.T #python提供了方便的转置与逆运算（.T/.I）return W 
X=np.mat([[1,1,1,1,1,1],times]) #测量时间矩阵（样本）
Y=np.mat(gravity) #重力数据矩阵（标签）
W=least_square(X,Y) 
import matplotlib.pyplot as plt #导入画图库函数
plt.rcParams['font.sans-serif']=['SimHei']#画图准备
plt.rcParams['axes.unicode_minus']=False
plt.scatter(times,gravity,color="green",label="重力值实际值",linewidth=2)
plt.plot(times,gravity,linewidth=1) #画实际重力测量数据
x1=np.linspace(20,110,5) #拟合直线x范围
y1=W[1,0]*x1+W[0,0] #拟合直线纵坐标取值
plt.plot(x1,y1,color="red",label="拟合直线",linewidth=2,linestyle=':')
plt.legend(loc='lower right') #画拟合直线
plt.show() #展示图像
new_times=[120,140,180] 
new_times=(np.mat(new_times)).T #需要预测的时间（新样本）
forecast_gravity=W[1,0]*new_times+W[0,0] #预测结果（预测值即标签）
print(forecast_gravity) #打印
loss_value1=0
for i in range(6):loss_value1 +=(W[1,0]*times[i]+W[0,0]-gravity[i])**2print(W[1,0]*times[i]+W[0,0])print(gravity[i]) #输出拟合数据与实际数据
print(loss_value1) #计算损失值

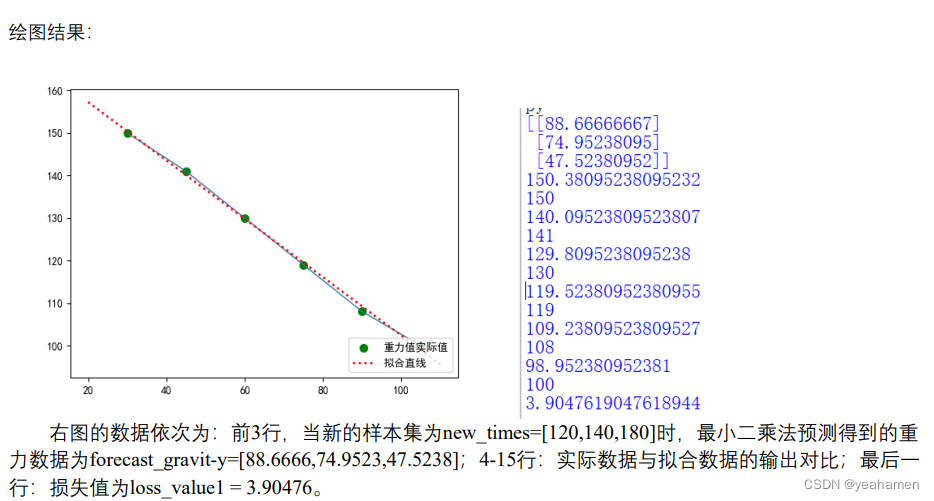
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！