1.快速排序

1.1 非经典：

• 每次选取数组的最后一个元素为基准，进行排序；
• 将大于基准的排后边，小于基准的排前面，等于基准的在中间（类似于荷兰国旗问题）；
• 直至进行排序的左边界=右边界。

package Sort;public class QuickSort {public static void main(String[] args) {int[] array= {1,5,4,8,3,2};quickSort(array,0,array.length-1);for(int i=0;i arr[r]) {swap(arr, --more, l);} else {l++;}}swap(arr, more, r);//交换基准和大于域的第一个位置的元素return new int[] {less + 1, more};}public static void swap(int[] arr,int i,int j) {int temp=arr[i];arr[i]=arr[j];arr[j]=temp;}
}

运行结果：

1.2 经典的：

第一次排序之前：

第一次排序之后：

第二次进行排序的范围：

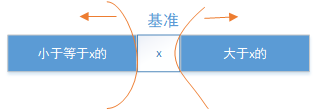
即：每次排序只搞定一个数x。（可能小于等于x之中还有多个等于x的）。

而上面1.1的方法，排完序后：

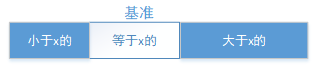
第二次排序的范围：

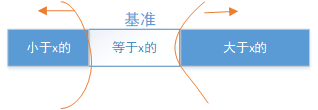
减少了比较的次数，提高了效率。

1.3 代码中的partation

刚开始时，less和more的位置：

一次排序之后：

交换x和大于区域的第一个位置的元素：

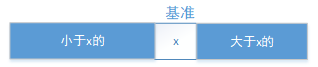
可以相对减少比较次数。

1.4 改进：随机快排（最常用的）

1.4.1 快排的缺陷

可能使得一部分区域没数据，基准值选的太偏。

比如：

此时选择7作为基准，一次排序后，只搞定了一个元素。花费是：

N个元素的花费为：，即。

1.4.2 最好的情况

大于小于区域长度相当——类似于归并排序的时间复杂度。

1.4.3 改进quickSort()

public static void quickSort(int[] arr, int l, int r) {if (l < r) {swap(arr, l + (int) (Math.random() * (r - l + 1)), r);//获取随机的元素为基准int[] p = partition(arr, l, r);quickSort(arr, l, p[0] - 1);quickSort(arr, p[1] + 1, r);}
}

每次不是选择最后位置，而是选择随机位置的数进行划分。

交换这个随机位置的数和最后位置元素的原因：便于代码复用。

落在每个位置上的概率相等，最终的时间复杂度应用概率表示，结果：。

最常用的，代码简洁——常数项很低。

• mergeSort：需准备一个数组，并且要数组拷贝；空间复杂度是
• quickSort：一个while搞定；空间复杂度：；
  • 随机快排的时间复杂度是那个；
  • 记住等与区域的左右边界，原因：
    • 当左半部分排完后，需要知道右半部分从哪开始；
  • 浪费空间的地方是在划分点。总共是划分次（概率计算）
    • 最坏是次；
    • 最好是次。

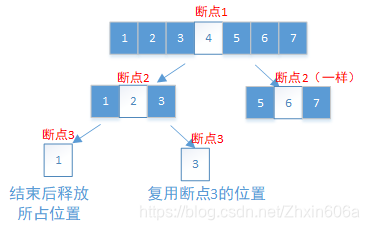
最少也得用3个位置存放断点。

1.5 算法在设计时绕开样本本身数据状况的方法

1.随机，打乱数据状况；

2.哈希，也是打乱。

1.6 其他

工程上用的是快排的非递归版本。

因为递归的准备代价高：压栈信息多，大量都是无用信息。

递归层数多时系统栈也会报错。

应该为非递归。

2.堆排序

堆：是完全二叉树（要么是一个满二叉树，要么仅有的节点序号和满二叉树中的一一对应）。

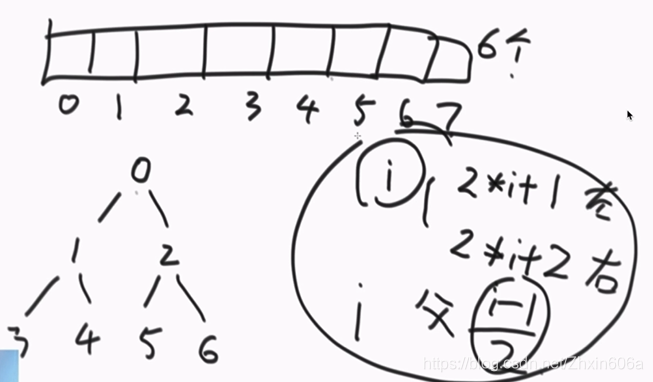
并不存在实际的二叉树，都是数组结构，只是在数组结构中定义了一个规则。

2.1 堆的分类

大根堆：任何一个子树的最大值都是头部；

小根堆：任何一个子树的最小值都是头部；

2.2 数组变成大根堆：

数组中的一个子数组也可想成完全二叉树。

原始数组：

1、首先，假设需要变换的数组的范围仅是0位置的元素：

（脑海中的：）

2、接着是0~1位置的元素：

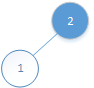
同时需要比较1和它父节点元素的大小，若大于就得交换。

父节点位置的确定：（当前元素的下标-1）/2

(1-1)/2=0；

所以1位置的元素和0位置的进行比较：1<2，不用交换

3、接着假设需要转换的是0~2位置的元素：

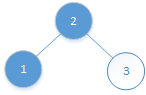
比较2位置的元素和(2-1)/2=0（向下取整）位置的元素：3>2，需要交换：

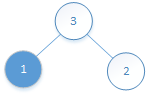
交换后，比较被交换位置0的元素和它父节点位置(0-1)/2=0的元素，相等，不满足大于的条件，不交换。

4、0~3位置的元素：

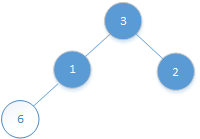
比较3位置的元素和(3-1)/2=1位置的元素：6>1，需要交换：

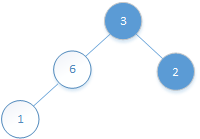
再接着比较6和它父节点0的元素：6>3，继续交换：

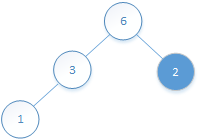
5、0~4位置的元素：

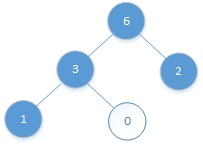
0小于它父节点位置(4-1)/2=1的元素3，所以不用交换。

6、0~5位置的元素：

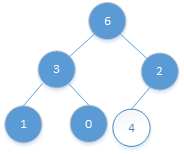
比较4和它父节点位置(5-1)/4=2的元素：4>2，需要交换：

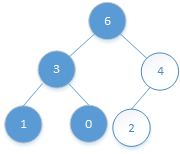
交换后，比较被交换节点位置2的元素和它父节点位置0的元素：4<6不需要交换。

5已经是数组的最大下标，大顶堆转换结束。

此部分的实现代码：

package Sort;public class HeapSort {public static void main(String[] args) {int[] array= {2,1,3,6,0,4};heapSort(array);for(int i=0;iarr[(i-1)/2]) {swap(arr,i,(i-1)/2);i=(i-1)/2;//变为自己的父节点，继续向上比较}}public static void swap(int[] arr,int i,int j) {int temp=arr[i];arr[i]=arr[j];arr[j]=temp;}
}

运行结果：

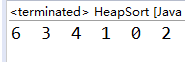
2.2.1 建立大根堆的时间复杂度

一个节点进来时，只需要和它到父节点、祖宗节点进行比较。

比较次数就为目前数高：

加入节点i时，面0~i-1的大顶堆已经建好，所以它比的就是0~i-1所形成的树高。

所以总共是：

2.3 heapify

当堆中有元素发生变化，进行调整的过程。

• 找到它的左右两个孩子；
• 孩子中较大的和它进行交换；

值变化之前：

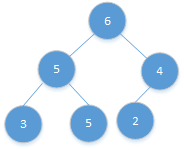
将6变为1：

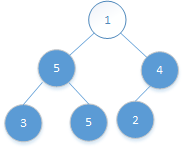
不满足大根堆的特性了，需要进行调整。

首先找到变化位置0的左右孩子：0*2+1=1，0*2+2=2。

比较，选择其中较大的和自己交换：5>4，所以1和5进行交换：

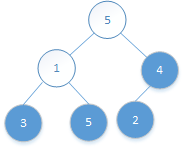
再找被调整位置1的左右孩子：1*2+1=3，1*2+2=4。

比较，找到其中较大的：5>3，所以1和5进行交换：

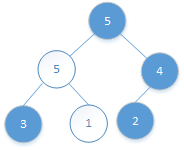
此时1位置4的左右孩子越界，计算停止。

大根堆调整完毕。

代码实现：

package Sort;public class HeapSort {public static void main(String[] args) {int[] array= {2,1,3,6,0,4};heapSort(array);for(int i=0;iarr[(i-1)/2]) {swap(arr,i,(i-1)/2);i=(i-1)/2;//变为自己的父节点，继续向上比较}}public static void heapify(int[] arr,int i,int heapsize) {int left=i*2+1;while(leftarr[j]?arr[i]:arr[j];return num>arr[k]?num:arr[k];}
}

运行结果：

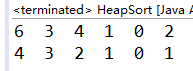
更简短的代码：

public static void heapify(int[] arr, int index, int size) {int left = index * 2 + 1;while (left < size) {//左孩子不越界//仅当右孩子不越界，并且右孩子大于左孩子时，largest=右孩子下标，//否则largest=左孩子下标int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;//largest处的元素再和index处的元素进行比较，largest为三者中最大值的下标largest = arr[largest] > arr[index] ? largest : index;//如果三者中最大值是index处的，结束循环if (largest == index) {break;}//largset!=index时才能执行到此处//交换index和三者中最大值的位置swap(arr, largest, index);//改变需要对比的节点的下标以及它左孩子的下标index = largest;left = index * 2 + 1;}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！