算法练习day20——190411(重建二叉树、斐波那契数列、跳台阶、矩形覆盖、变态跳台阶、旋转数组的最小数字、矩阵中的路径)
1、重建二叉树
根据二叉树的前序遍历和中序遍历的结果,重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
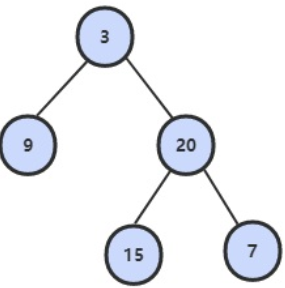
preorder = [3,9,20,15,7]、inorder = [9,3,15,20,7]
1.1 分析
前序遍历的第一个值为根节点的值,使用这个值将中序遍历结果分成两部分,左部分为树的左子树中序遍历结果,右部分为树的右子树中序遍历的结果。
1.2 代码实现
static class TreeNode{int value;TreeNode left;TreeNode right;public TreeNode(int value) {this.value=value;}
}
private Map indexForInOrders = new HashMap<>();
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {for (int i = 0; i < in.length; i++)indexForInOrders.put(in[i], i);//将前缀序列放入Map中,便于后面依据值得到它的indexreturn reConstructBinaryTree(pre, 0, pre.length - 1, 0);
}
private TreeNode reConstructBinaryTree(int[] pre, int preL, int preR, int inL) {if (preL > preR)return null;TreeNode root = new TreeNode(pre[preL]);int inIndex = indexForInOrders.get(root.value);int leftTreeSize = inIndex - inL;root.left = reConstructBinaryTree(pre, preL + 1, preL + leftTreeSize, inL);root.right = reConstructBinaryTree(pre, preL + leftTreeSize+ 1, preR, inL + leftTreeSize + 1);return root;
} 2.斐波那契数列
求斐波那契数列的第 n 项,n <= 39。
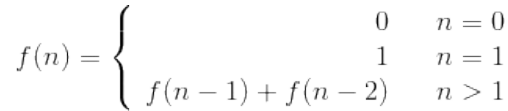
2.1 分析
如果使用递归求解,会重复计算一些子问题。例如,计算 f(10) 需要计算 f(9) 和f(8),计算 f(9) 需要计算 f(8) 和 f(7),可以看到 f(8) 被重复计算了。

2.2 代码实现
2.2.1 递归
递归是将一个问题划分成多个子问题求解
public static int process(int i) {if(i==0||i==1)return i;return process(i-1)+process(i-2);
}2.2.2 动态规划
动态规划也是将一个问题划分成多个子问题求解,但是动态规划会把子问题的解缓存起来,从而避免重复求解子问题。
public static int process1(int n) {if (n <= 1)return n;int[] fib = new int[n + 1];//0~n,第n+1个即fib[n]存的是最终的结果fib[1] = 1;for (int i = 2; i <= n; i++)fib[i] = fib[i - 1] + fib[i - 2];return fib[n];
}2.2.3 改进1
考虑到第 i 项只与第 i-1 和第 i-2 项有关,因此只需要存储前两项的值就能求解第 i项,从而将空间复杂度由 O(N) 降低为 O(1)。
public int process2(int n) {if (n <= 1)return n;int pre2 = 0, pre1 = 1;int fib = 0;for (int i = 2; i <= n; i++) {fib = pre2 + pre1;pre2 = pre1;pre1 = fib;} return fib;
}2.2.4 改进2
由于待求解的 n 小于 40,因此可以将前 40 项的结果先进行计算,之后就能以O(1) 时间复杂度得到第 n 项的值了。
public class Solution {private int[] fib = new int[40];public Solution() {fib[1] = 1;fib[2] = 2;for (int i = 2; i < fib.length; i++)fib[i] = fib[i - 1] + fib[i - 2];} public int Fibonacci(int n) {return fib[n];}
}3.跳台阶
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
3.1 分析
总共有n级台阶,f(n)中跳法。如果第一次跳1级,那么f(n)=f(n-1);若跳2级,则f(n)=f(n-2)。总:f(n)=f(n-1)+f(n-2)——斐波那契数列。
3.2 代码实现
public int JumpFloor(int n) {if (n <= 2)return n;int pre2 = 1, pre1 = 2;int result = 1;for (int i = 2; i < n; i++) {result = pre2 + pre1;pre2 = pre1;pre1 = result;} return result;
}4.矩形覆盖
我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。
请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形,总共有多少种方法?
4.1 分析
将2*n这个大矩形,看成一个n个矩形线性排列,然后一次可以用一个小1*1的矩形覆盖(即:2*1的矩形竖着),也可以用2*1的矩形覆盖(2*1的矩形横着)。这就和跳台阶一样。如图所示:

4.2 代码实现
public int RectCover(int n) {if (n <= 2)return n;int pre2 = 1, pre1 = 2;int result = 0;for (int i = 3; i <= n; i++) {result = pre2 + pre1;pre2 = pre1;pre1 = result;} return result;
}5.变态跳台阶
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级... 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
5.1 分析(原博)
用f(n)表示青蛙跳上n阶台阶的跳法数,设定f(0) = 1;
当n = 1 时,只有一种跳的方式,一阶跳,f(1) = f(0) =1;
当n = 2 时,有两种跳的方式,一阶跳和两阶跳,f(2) = f(1) + f(0) = 2;
当n = 3 时,有三种跳的方式,第一次跳出一阶后,后面还有f(3-1)中跳法; 第一次跳出二阶后,后面还有f(3-2)中跳法;第一次跳出三阶后,后面还有f(3-3)中跳法,f(3) = f(2) + f(1) + f(0) = 4;
当n = n 时,第一次跳出一阶后,后面还有f(n-1)中跳法; 第一次跳出二阶后,后面还有f(n-2)中跳法......第一次跳出n阶后,后面还有 f(n-n)中跳法,即:
f(n) = f(n-1) + f(n-2) + f(n-3) + ... + f(n-n) = f(0) + f(1) + f(2) + ... + f(n-1)
又因为 f(n-1) = f(0) + f(2) + f(3) + ... + f(n-2)
两式相减得:f(n) = 2 * f(n-1) ( n >= 2)
| 0,n = 0
f(n) = | 1, n = 1
| 2 * f(n-1) , n >= 2
5.2 代码实现
public static int JumpFloor1(int target) if(target<=1)return target;int result=1;for (int i = 2; i <= target; i++)result+=result;return result;
}6.旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组 {3, 4, 5, 1, 2} 为 {1, 2, 3, 4, 5} 的一个旋转,该数组的最小值为 1。
6.1 分析
在一个有序数组中查找一个元素可以用二分查找,二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度都为 O(logN)。
本题可以修改二分查找算法进行求解:
- 当 nums[m] <= nums[h] 的情况下,说明解在 [l, m] 之间,此时令 h = m;
- 否则解在 [m + 1, h] 之间,令 l = m + 1。
6.2 代码实现
public class minNumber {public static void main(String[] args) {int [] arr= {3,4,5,1,2};System.out.print(findMinNumber(arr));}public static int findMinNumber(int[] arr) {if(arr.length==0||arr==null)return -1;int l=0;int h=arr.length-1;while(l6.3 允许重复元素
如果数组元素允许重复的话,那么就会出现一个特殊的情况:nums[l] == nums[m]== nums[h],那么此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
public static int findMinNumber(int[] arr) {if(arr.length==0||arr==null)return -1;int l=0;int h=arr.length-1;while(l nums[i + 1])//出现前大于后的情况,后者肯定为最小return nums[i + 1];return nums[l]
} 7.矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。
路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
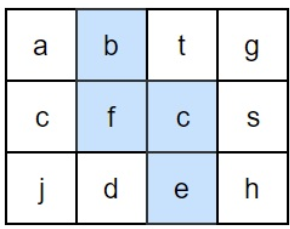
例如下面的矩阵包含了一条 bfce 路径:
7.1 分析(原博)
这是一个可以用回溯法解决的典型问题。
首先,遍历这个矩阵matrix,我们很容易就能找到与字符串str中第一个字符相同的矩阵元素ch。
然后遍历ch的上下左右四个字符,如果有和字符串str中下一个字符相同的,就把那个字符当作下一个字符(下一次遍历的起点),如果没有,就需要回退到上一个字符,然后重新遍历。
为了避免路径重叠,需要一个辅助矩阵来记录路径情况。
当矩阵坐标为(row,col)的格子和路径字符串中下标为pathLength的字符一样时,从4个相邻的格子(row,col-1)、(row-1,col)、(row,col+1)以及(row+1,col)中去定位路径字符串中下标为pathLength+1的字符。
如果4个相邻的格子都没有匹配字符串中下标为pathLength+1的字符,表明当前路径字符串中下标为pathLength的字符在矩阵中的定位不正确,我们需要回到前一个字符串(pathLength-1),然后重新定位。
一直重复这个过程,直到路径字符串上所有字符都在矩阵中找到格式的位置(此时str[pathLength] == '\0')。
7.2 代码实现(原博)
public class StringPathInMatrix {public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {if (matrix == null || rows < 1 || cols < 1 || str == null) {return false;}boolean[] isVisited = new boolean[rows * cols];for (boolean v : isVisited) {v = false;}int pathLength = 0;for (int row = 0; row < rows; row++) {for (int col = 0; col < cols; col++) {if (hasPathCore(matrix, rows, cols, row, col, str, pathLength, isVisited))return true;}}return false;}private boolean hasPathCore(char[] matrix, int rows, int cols, int row, int col, char[] str, int pathLength,boolean[] isVisited) {if (row < 0 || col < 0 || row >= rows || col >= cols || isVisited[row * cols + col] == true|| str[pathLength] != matrix[row * cols + col])return false;if (pathLength == str.length - 1)return true;boolean hasPath = false;isVisited[row * cols + col] = true;hasPath = hasPathCore(matrix, rows, cols, row - 1, col, str, pathLength + 1, isVisited)|| hasPathCore(matrix, rows, cols, row + 1, col, str, pathLength + 1, isVisited)|| hasPathCore(matrix, rows, cols, row, col - 1, str, pathLength + 1, isVisited)|| hasPathCore(matrix, rows, cols, row, col + 1, str, pathLength + 1, isVisited);if (!hasPath) {isVisited[row * cols + col] = false; }return hasPath;}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!