ICML22:Finding Global Homophily in Graph Neural Networks When Meeting Heterophily 华师 MSRA NTU
文章信息

1.摘要
本文是异质图研究,写作措辞上较为易懂。异质图2020年-2021较多,本文方法1.设计不同节点间的 相似度聚合矩阵,以一种globa视角。 这个矩阵正负数,有闭合解。 2. 优化后 线性复杂度。 3. 有grouping effect
亮点:1. 可扩展异质图 2. 对比了nips21的Linkx(也是采用双MLP类似LINXK),并采用了新提出的数据集 3.实验很详尽。
2.介绍
先介绍了graph发展,说出gcn、gat、graphsage的smoothing平滑不适合异质性。说出几个解决办法,高通滤波+多跳邻居,LINX,GPRGNN,nips或者iclr的方法。 但是如何确定 不同节点的 邻居范围还是很难。 引出这个 邻居矩阵,进而优化线性,并与 一个工作相关联,有group effct。

3.related work
GNN典型研究+各种小方向

异质图
有GPRGNN(pagerank一类,各阶邻居的权重不同) ACM-GCN(高低通滤波) H2GCN(应该复杂度很大) WRGAT,GGCN(signed message) LINKX(MLP+graph)
本文的 GloGNN不同:是邻居聚合从 整个图节点,考虑了更多的相同类作为邻居,提高了gnn在异质图上的表现。

4. 预定义
介绍graph+同质性衡量
5.方法
双MLP学习 X和A ,拼接后进行卷积
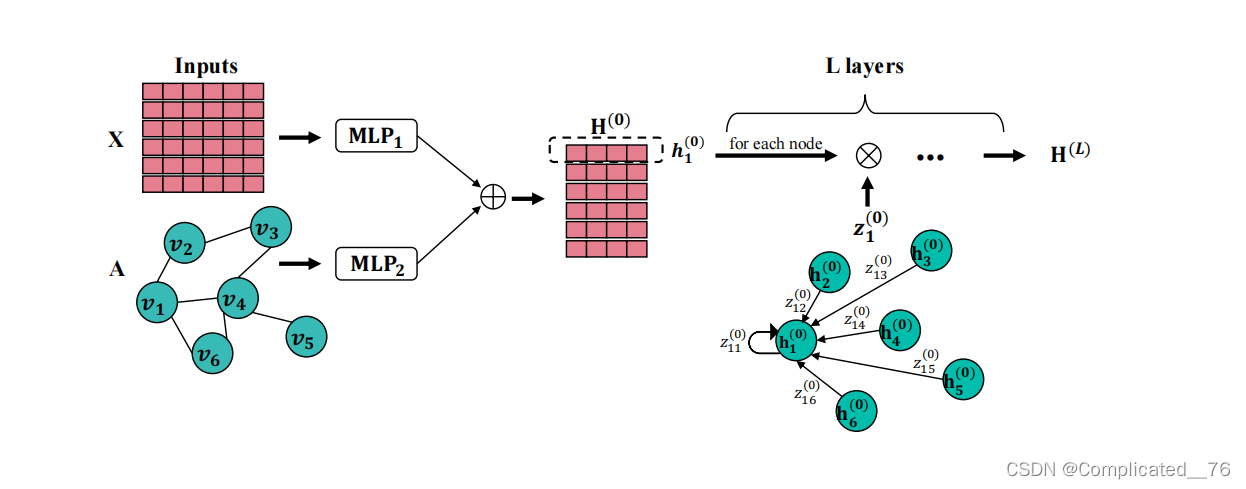
5.1 系数矩阵
子空间的方法: 一个节点 能够通过 其他节点和 噪声表示O

双MLP包含AX, 同时参考了APPNP,加上了初始残差

同时考虑多步可达,这里出发点是, 子结构相同 ,两个远的节点也相似 Ak是多跳矩阵,幂次

第一项是 减小噪声O,第二项是F范数,第三项是 正则化Z ,通过多跳的Ak
得出闭合解,
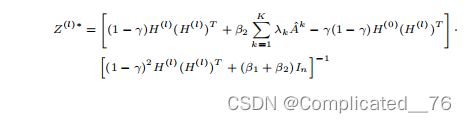
5.2 优化
修改1
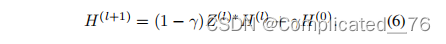
时间复杂度2次求Z*,三次求矩阵相乘。 通过转换6到7
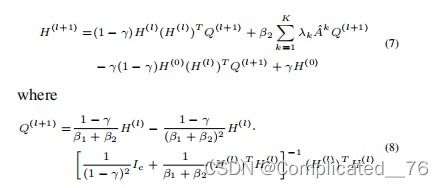
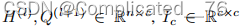
矩阵求逆是在Rc×c中的一个时间复杂度仅为O(c3)的矩阵上进行的。c通常是一个非常小的数字。这大大提高了模型的效率。
7.8公式 矩阵相乘的结合律,从右向左进行计算。减小复杂度。 H的转置Q是cnnc=cc,和前面的nc是nc2. 如果从左往右是nccn nc=n2c
7式的第二项:稀疏A和q相乘是nc。A的平均每行的非零元素是k1.
7式总的时间复杂度=c3+nc2(?)+nc2(7的第一、三项)+k1cn(第二项)=n(c2+c2+k1c)=nk2<
7式总的时间复杂度=c3+nc2(?)+nc2(7的第一、三项)+k1cn(第二项)=n(c2+c2+k1c)=nk2<
5.3 group effect
结合作者之前自己的一片KDD,说明Z*、 H 都具有group effect

对于任意两个节点vi和vj,无论它们在图中有多远,如果它们共享相似的特征向量和局部结构,我们都可以得出结论:(1),它们将被给予相似的系数向量;(2),它们将在描述其他节点时扮演相似的角色;而(3),它们将得到相似的表示向量。
另一方面,在具有异质性的图中,相邻的节点更有可能出现不同的情况,因此它们会得到不同的嵌入。此外,对于特征相似度较低的两个节点,如果它们具有较高的结构相似性,则可以通过局部图结构的正则化项来增强其表征
5.4 gloGNN++
之前的这个H矩阵是 纵向的 attention,即 节点和 邻居之间的。 这里提出 横向的 attention, 就是 自身节点特征的 重要性不同, 采用常规的方法,增加一个 对角矩阵,作为每一维 特征的 attention

5.5 discussion
1.GAT中的权重是自动学习的,缺乏可解释性,但我们的模型中的Z(l)是来自一个精心设计良好的优化问题,并且有一个封闭的解
2.其次,GAT中的注意权值总是非负值,而我们的方法中的Z(l)允许有符号值。因此,GAT只使用低通卷积滤波器,而我们的方法同时结合了低通和高通滤波器。
3.第三,对于每个节点,GAT对图中所有节点执行的邻域聚合计算代价昂贵,具有二次时间复杂度w.r.t.节点数。然而,我们的方法加速了聚合,并推导出了一个线性的时间复杂度
6.实验
6.1 数据集+对比算法
采用15个 ccp+6小 异质图 +6大 异质图(LINKX)
对比方法 涵盖了 GNN-classical , 异质图的方法+mlp

6.2 精度
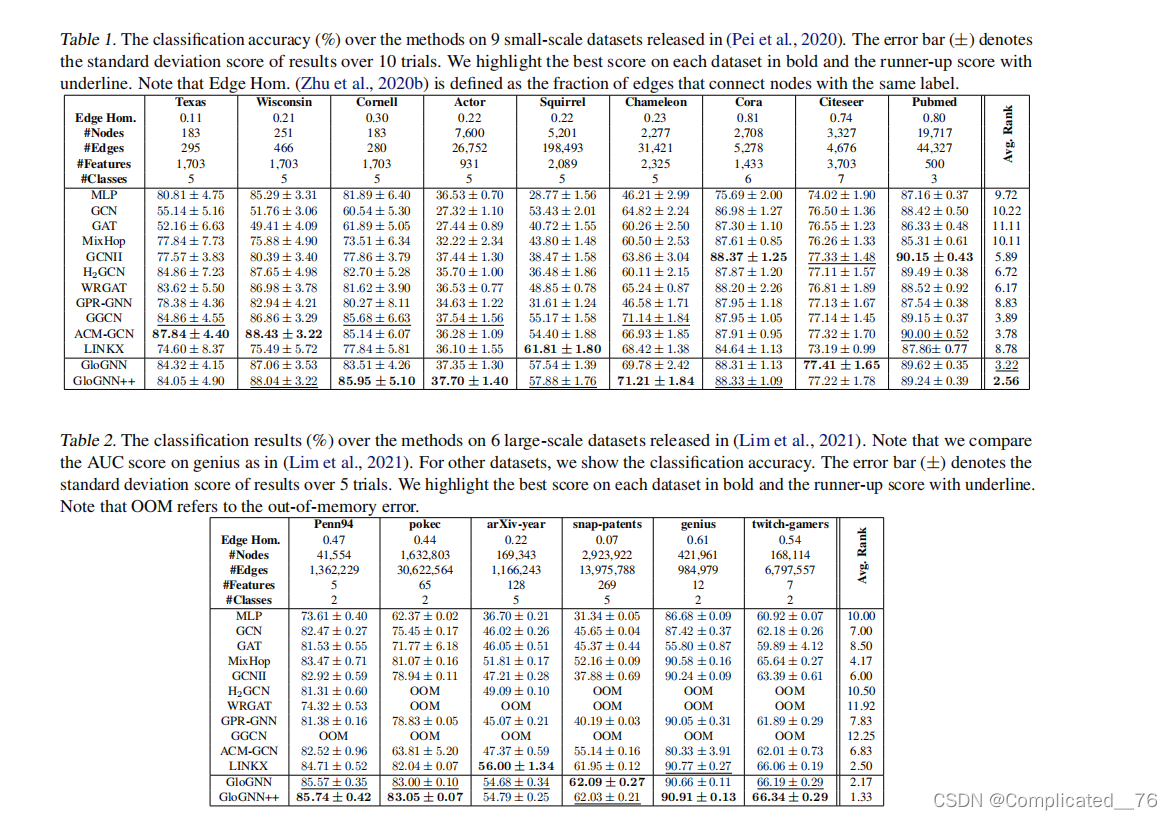
6.3 时间
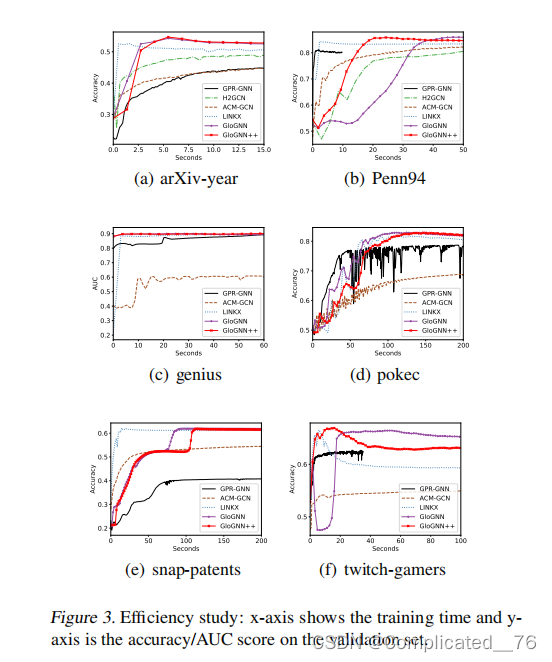
6.4 group effect
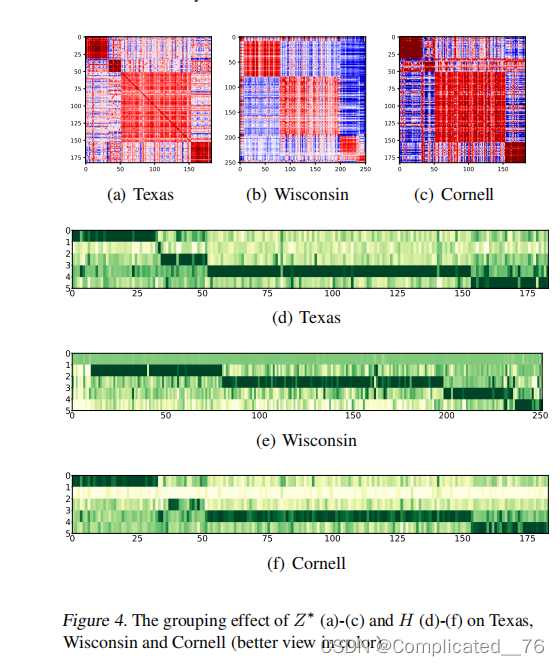
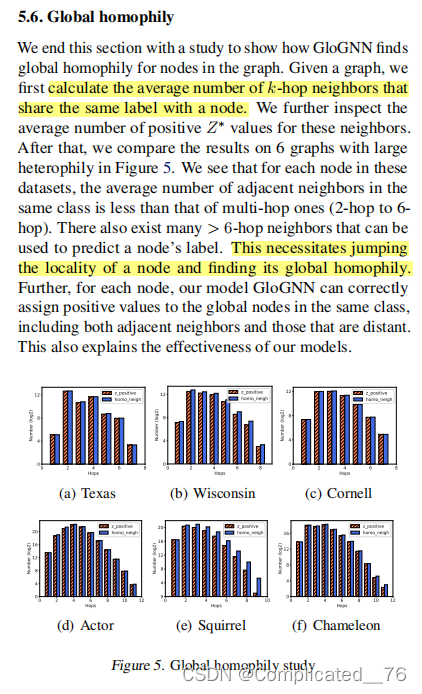
6.5 阐明 跳出局部找全局的 必要性
存在很多 超过1跳(局部)的相似性节点可以 都被使用
本文通过 子空间的方法 来 衡量 邻居间的 attention 线性优化后减少了复杂度。 机器学习 也存在解释性
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!