平面线段相交
一、相交测试
相交成立条件:
- a b ⃗ 跨 立 c d ⃗ ; \vec{ab}跨立\vec{cd}; ab跨立cd;
- c d ⃗ 跨 立 a b ⃗ ; \vec{cd}跨立\vec{ab}; cd跨立ab;
两个条件同时成立,说明线段ab与线段cd相交。
参考下图所示
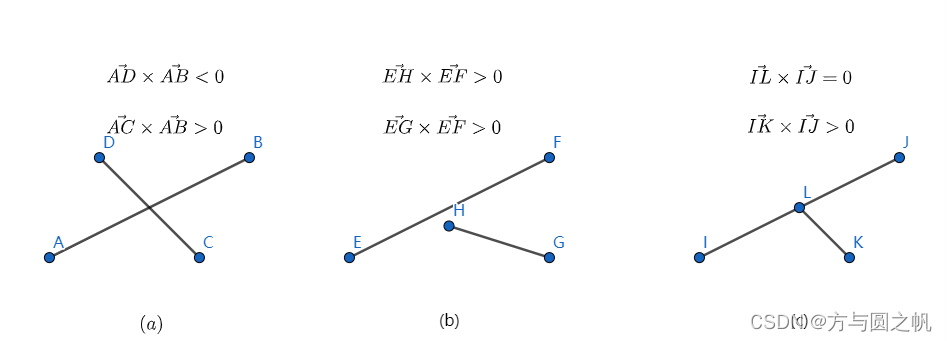
- 图(a) 段AB 与 段CD相交
A D ⃗ × A B ⃗ < 0 , 即 点 D 在 段 A B 的 左 手 边 ; \vec{AD} \times \vec{AB} < 0,即点D在段AB的左手边; AD×AB<0,即点D在段AB的左手边;
A C ⃗ × A B ⃗ > 0 , 即 点 C 在 段 A B 的 右 手 边 ; \vec{AC} \times \vec{AB} > 0,即点C在段AB的右手边; AC×AB>0,即点C在段AB的右手边;
即 C D ⃗ 跨 立 A B ⃗ . 即\vec{CD} 跨立 \vec{AB}. 即CD跨立AB.
C A ⃗ × C D ⃗ < 0 , 即 点 A 在 段 C D 的 左 手 边 ; \vec{CA} \times \vec{CD} < 0,即点A在段CD的左手边; CA×CD<0,即点A在段CD的左手边;
C B ⃗ × C D ⃗ > 0 , 即 点 B 在 段 C D 的 右 手 边 ; \vec{CB} \times \vec{CD} > 0,即点B在段CD的右手边; CB×CD>0,即点B在段CD的右手边;
即 A B ⃗ 跨 立 C D ⃗ . 即\vec{AB} 跨立 \vec{CD}. 即AB跨立CD.
- 图(b) 段EF 与 段GH不相交
E H ⃗ × E F ⃗ > 0 , 即 点 H 在 段 E F 的 右 手 边 ; \vec{EH} \times \vec{EF} > 0,即点H在段EF的右手边; EH×EF>0,即点H在段EF的右手边;
E G ⃗ × E F ⃗ > 0 , 即 点 G 在 段 E F 的 右 手 边 ; \vec{EG} \times \vec{EF} > 0,即点G在段EF的右手边; EG×EF>0,即点G在段EF的右手边;
即 G H ⃗ 不 跨 立 E F ⃗ . 即\vec{GH} 不跨立 \vec{EF}. 即GH不跨立EF.
G E ⃗ × G H ⃗ < 0 , 即 点 E 在 段 G H 的 左 手 边 ; \vec{GE} \times \vec{GH} < 0,即点E在段GH的左手边; GE×GH<0,即点E在段GH的左手边;
G F ⃗ × G H ⃗ > 0 , 即 点 F 在 段 G H 的 右 手 边 ; \vec{GF} \times \vec{GH} > 0,即点F在段GH的右手边; GF×GH>0,即点F在段GH的右手边;
即 E F ⃗ 跨 立 G H ⃗ . 即\vec{EF} 跨立 \vec{GH}. 即EF跨立GH.
- 图(c 段IJ 与 段KL相交
I L ⃗ × I J ⃗ = 0 , 即 点 L 在 段 I J 上 ; \vec{IL} \times \vec{IJ} = 0,即点L在段IJ上; IL×IJ=0,即点L在段IJ上;
I K ⃗ × I J ⃗ > 0 , 即 点 K 在 段 I J 的 右 手 边 ; \vec{IK} \times \vec{IJ} > 0,即点K在段IJ的右手边; IK×IJ>0,即点K在段IJ的右手边;
即 K L ⃗ 跨 立 I J ⃗ . 即\vec{KL} 跨立 \vec{IJ}. 即KL跨立IJ.
K I ⃗ × K L ⃗ < 0 , 即 点 I 在 段 K L 的 左 手 边 ; \vec{KI} \times \vec{KL} < 0,即点I在段KL的左手边; KI×KL<0,即点I在段KL的左手边;
K J ⃗ × K L ⃗ > 0 , 即 点 J 在 段 K L 的 右 手 边 ; \vec{KJ} \times \vec{KL} > 0,即点J在段KL的右手边; KJ×KL>0,即点J在段KL的右手边;
即 I J ⃗ 跨 立 K L ⃗ . 即\vec{IJ} 跨立 \vec{KL}. 即IJ跨立KL.
二、 求取交点
假定段AB交段CD,考虑下图所示:
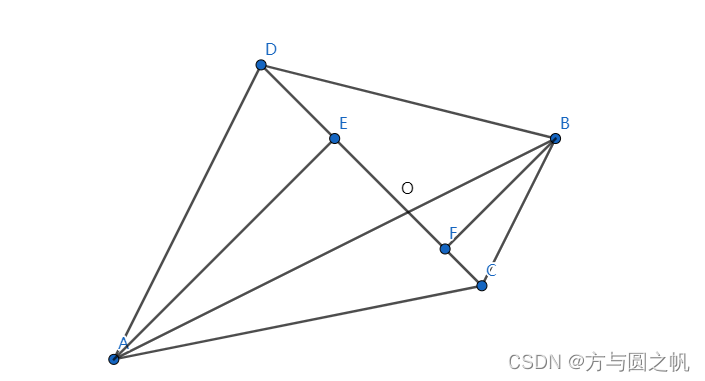
设 段 A B 交 段 C D , A E ⊥ C D , B F ⊥ C D 。 设 段AB交段CD,AE\bot CD,BF\bot CD。 设段AB交段CD,AE⊥CD,BF⊥CD。
∵ △ A E O ∼ △ B F O , ∴ ∣ A E ⃗ ∣ ∣ B F ⃗ ∣ = ∣ A O ⃗ ∣ ∣ B O ⃗ ∣ 。 \because \bigtriangleup{AEO} \sim \bigtriangleup{BFO},\therefore \frac{|\vec{AE}|}{|\vec{BF}|} = \frac{|\vec{AO}|}{|\vec{BO}|}。 ∵△AEO∼△BFO,∴∣BF∣∣AE∣=∣BO∣∣AO∣。
又 ∵ S △ A C D = 0.5 ∗ ∣ A E ⃗ ∣ ∗ ∣ C D ⃗ ∣ = 0.5 ∗ ∣ C A ⃗ × C D ⃗ ∣ 又\because S_{\bigtriangleup{ACD}} = 0.5 * |\vec{AE}| * |\vec{CD}|=0.5 * |\vec{CA} \times \vec{CD}| 又∵S△ACD=0.5∗∣AE∣∗∣CD∣=0.5∗∣CA×CD∣
且 S △ C D B = 0.5 ∗ ∣ B F ⃗ ∣ ∗ ∣ C D ⃗ ∣ = 0.5 ∗ ∣ C B ⃗ × C D ⃗ ∣ 且S_{\bigtriangleup{CDB}} = 0.5 * |\vec{BF}| * |\vec{CD}| = 0.5 * |\vec{CB} \times \vec{CD}| 且S△CDB=0.5∗∣BF∣∗∣CD∣=0.5∗∣CB×CD∣
∴ λ = ∣ A O ⃗ ∣ ∣ B O ⃗ ∣ = S △ A C D S △ C D B = ∣ C A ⃗ × C D ⃗ ∣ ∣ C B ⃗ × C D ⃗ ∣ \therefore \lambda =\frac{|\vec{AO}|}{|\vec{BO}|}=\frac{S_\bigtriangleup{ACD}}{S_\bigtriangleup{CDB}} = \frac{|\vec{CA} \times \vec{CD}|}{|\vec{CB} \times \vec{CD}|} ∴λ=∣BO∣∣AO∣=S△CDBS△ACD=∣CB×CD∣∣CA×CD∣
∴ A O ⃗ = λ O B ⃗ \therefore \vec{AO} = \lambda\vec{OB} ∴AO=λOB
∴ A B ⃗ = A O ⃗ + O B ⃗ = A O ⃗ + λ A O ⃗ = ( 1 + λ ) A O ⃗ \therefore \vec{AB} = \vec{AO} + \vec{OB} = \vec{AO} + \lambda\vec{AO}=(1+\lambda)\vec{AO} ∴AB=AO+OB=AO+λAO=(1+λ)AO
∴ A O ⃗ = 1 1 + λ A B ⃗ \therefore \vec{AO}= \frac{1}{1+\lambda}\vec{AB} ∴AO=1+λ1AB
即 即 即
( O x − A x , O y − A y ) = 1 1 + λ ( B x − A x , B y − A y ) (O_x-A_x,O_y-A_y) = \frac{1}{1+\lambda}(B_x-A_x,B_y-A_y) (Ox−Ax,Oy−Ay)=1+λ1(Bx−Ax,By−Ay)
可 推 出 可推出 可推出
O x = A x + 1 1 + λ ( B x − A x ) O_x = A_x + \frac{1}{1+\lambda}(B_x-A_x) Ox=Ax+1+λ1(Bx−Ax)
O y = A y + 1 1 + λ ( B y − A y ) O_y = A_y + \frac{1}{1+\lambda}(B_y-A_y) Oy=Ay+1+λ1(By−Ay)
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!