CCF CSP认证2022年12月题解 聚集方差（树上启发式合并）

T4 聚集方差

思路

树上启发式合并，multiset上二分。

注意到$n$的数据范围为3e5，聚集方差实际上是在一个可重复集合（一棵子树的所有节点）中找每个数最相近的数，我一开始想到了用multiset上二分，但是对每棵子树都操作一次总的时间复杂度为 O ( n 2 l o g n ) O(n^2logn) O(n2logn)，显然不能满足要求。

首先，明确一点，multiset必须复用，用完之后清空，否则空间复杂度是 O ( n 2 ) O(n^2) O(n2)。这里multiset可以理解为用于计算ans的info。

从时间复杂度的角度，注意到为什么要求在一棵树上实现这个操作？

子树和子树有相互包含的关系，可以据此实现一些信息的复用，比如下图，如果我在操作以2号节点为根的子树之后去操作整棵树（即以1号节点为根的子树），此时，并不需要清空multiset，可以复用，只需要将3号节点加入集合。

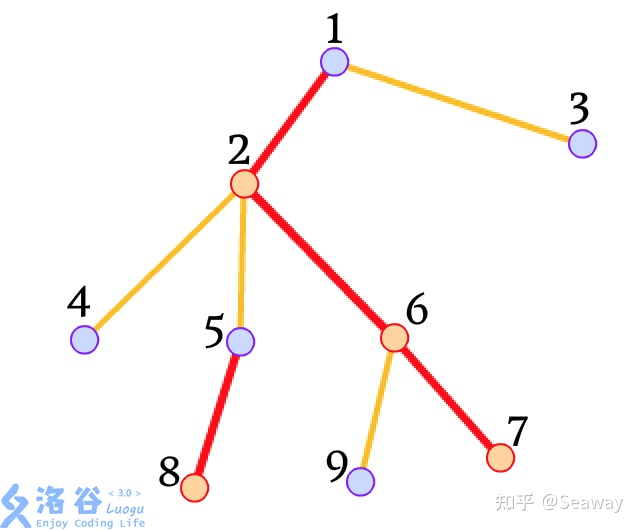
递归计算某个节点的子节点的ans后，最后一个子节点的info是可以复用的。最后一个节点越大，可复用的info就越多，时间也就越优。因此，最优做法是将重儿子放在最后遍历，返回之后不清空info，也就是multiset。这就是树上启发式合并。

树上启发式合并（dsu on tree）

【图论】树上启发式合并

时间复杂度分析

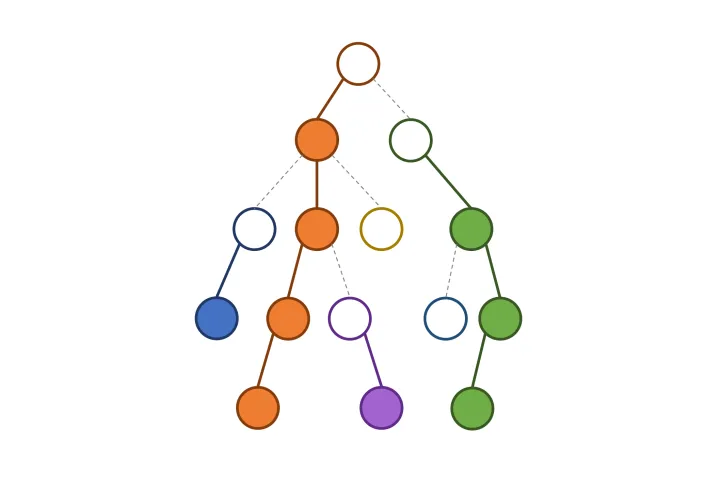
树链剖分的一个结论，一个节点到根节点最多经过$logn$条轻边。这是因为，如果一个节点连向父节点的边是轻边，则存在一个子树大小不小于它的兄弟节点，那么父节点的子树大小至少是该节点的2倍。因此，每经过一条轻边，子树大小就翻倍，所以最多经过$logn$条轻边。（有些博客说，dsu同dsu on tree没有关系，个人认为这是这两个算法想法上的相通之处，暴力而优雅）

所以，每个节点作为轻子树上的节点最多只会被遍历$logn$次（反过来分析），dfs所有节点访问一次，addsubtree只会遍历轻子树上的节点，而delsubtree和addsubtree一一对应，所以复杂度从 O ( n 2 ) O(n^2) O(n2)降低为$O(nlogn)$，乘上计算info（set上二分操作）的复杂度，该问题中总时间复杂度为$O(n\times logn\times logn)$，约为1e7。

set 上二分

之前3月份的t4也考了这个。

这次用了一个技巧，在集合中先加入$inf$和$-inf$，简化对lower_bound方法返回值的判断。

首先，观察到加入一个节点，只可能改变值相邻两个节点的聚集方差贡献，设加入的数为$b$，在multiset相邻的5个数（包含自己）为 b 1 , b 2 , b , b 4 , b 5 b_1,b_2,b,b_4,b_5 b1​,b2​,b,b4​,b5​
这里实际上 b i b_i bi​并不存在，因此init时往集合中加入两个$inf$和$-inf$，保证 b i b_i bi​是一个数。
这里， b 2 , b 4 b_2,b_4 b2​,b4​对聚集方差的贡献可能改变，$b$可能成为它们的匹配。因此，我们在聚集方差中先减去，然后再连同$b$的贡献一起重新计算。

代码

const int N = 3e5 + 5;
const int inf = 0x3f3f3f3f;vector<int> g[N];
int a[N];
int dep[N], sz[N], hson[N];
multiset<int> mset;
ll ans[N], sum;void init() {mset.insert(inf), mset.insert(inf);mset.insert(-inf), mset.insert(-inf);
}void dfs0(int u, int fa = -1) {int mx = 0, size = 1;for (auto v : g[u]) {if (v != fa) {dfs0(v, u);size += sz[v];if (sz[v] > mx) {hson[u] = v, mx = sz[v];}}}sz[u] = size;
}ll calu(ll x, ll y, ll z) {if (abs(y) == inf) { return 0; }if (abs(x) != inf && abs(z) != inf) {return min((y - z) * (y - z), (y - x) * (y -x));}else if (abs(x) != inf && abs(z) == inf) {return (y - x) * (y - x);}else if (abs(x) == inf && abs(z) != inf) {return (y - z) * (y - z);}else { return 0; }
}void add(int u) {// 加入一个节点，只可能改变值相邻两个节点的聚集方差增量auto it = mset.lower_bound(a[u]);// 找到第一个不小于a[u]值it--, it--;ll b[6];b[1] = *it, it++;b[2] = *it, it++;b[3] = a[u];b[4] = *it, it++;b[5] = *it, it++;sum -= calu(b[1], b[2], b[4]);sum -= calu(b[2], b[4], b[5]);sum += calu(b[1], b[2], b[3]);sum += calu(b[2], b[3], b[4]);sum += calu(b[3], b[4], b[5]);mset.insert(a[u]);
}
void del(int u) {
}void addsubtree(int u, int fa = -1) {add(u);for (auto v : g[u]) {if (v != fa) addsubtree(v, u);}
}
void delsubtree(int u, int fa = -1) {del(u);for (auto v : g[u]) {if (v != fa) delsubtree(v, u);}
}void dfs(int u, int fa = -1, bool keep = -1) {// keep标志信息是否保留// 先遍历轻儿子for (auto v : g[u]) {if (v != fa && v != hson[u]) {dfs(v, u, 0);}}// 最后遍历重儿子if (hson[u]) { dfs(hson[u], u, 1); }add(u);for (auto v : g[u]) {if (v != fa && v != hson[u]) {addsubtree(v, u);}}   // 重儿子的信息没有删除，因此不必再添加ans[u] = sum;if (!keep) {// delsubtree(u, fa);// clearupmset.clear(); init();sum = 0;}
}void solve() {int n; cin >> n;int v;for (int u = 2; u <= n; u++) {cin >> v;g[u].push_back(v);g[v].push_back(u);}for (int i = 1; i <= n; i++) cin >> a[i];dfs0(1);init();dfs(1);for (int i = 1; i <= n; i++) {cout << ans[i] << '\n';}
}

reference
浅谈树链剖分
算法学习笔记(86): 树上启发式合并
算法学习笔记(59): 重链剖分

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！