rust怎么传送坐标_德国人怎么学电机——浅谈电机模型(十一)：异步电机：绕线转子电机(一)...

交流电机概述传送门：

善道：德国人怎么学电机——浅谈电机模型(七)：交流电机概述​zhuanlan.zhihu.com

旋转磁场理论传送门：

善道：德国人怎么学电机——浅谈电机模型(八)：三相交流电机的旋转磁场理论(一)旋转磁动势​zhuanlan.zhihu.com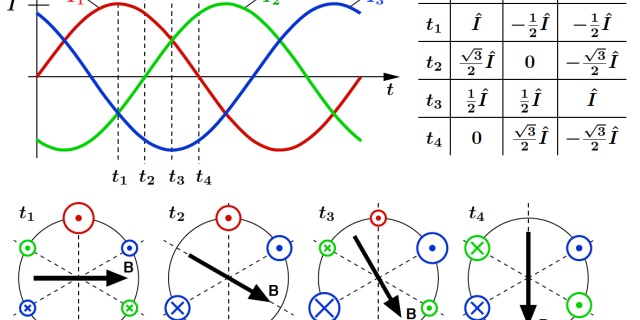善道：德国人怎么学电机——浅谈电机模型(九)：三相交流电机的旋转磁场理论(二)绕组因数​zhuanlan.zhihu.com善道：德国人怎么学电机——浅谈电机模型(十)：三相交流电机的旋转磁场理论(三)旋转磁场和转矩​zhuanlan.zhihu.com

---

从这一章我们开始讨论异步电机。

从机械结构上看，异步电机里有两种常用的形式，一种是转子直接使用导体棒构成类似于鼠笼的鼠笼式异步电机(Asynchromaschine mit Käfigläufer)，以及另一种使用了与定子三相绕组同款的对称绕组的绕线转子电机(Asynchromaschine mit Schleifringläufer)。

1.带绕线滑环的异步电机

1.1绕线转子电机的机械结构

如同前面的旋转磁场部分所言，异步电机最明显的特征就是：异步电机的转子转数不必须与同步转数相等。即所谓的“异步”(Asynchro-)。异步电机是如今最广泛分布的电动机，因为总的来说，最常使用的鼠笼式转子是一种抗扰动、少维护、可超载、制造方便的简单设计。但由于鼠笼式异步电机的感应电流是在整个转子导体上的涡流，分析起来比较复杂，所以我们先从绕线转子电机开始讨论。

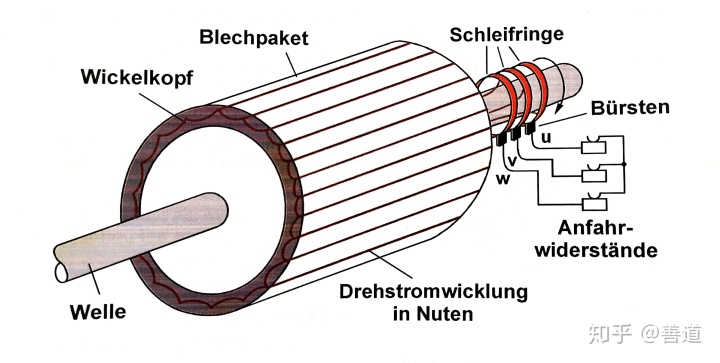
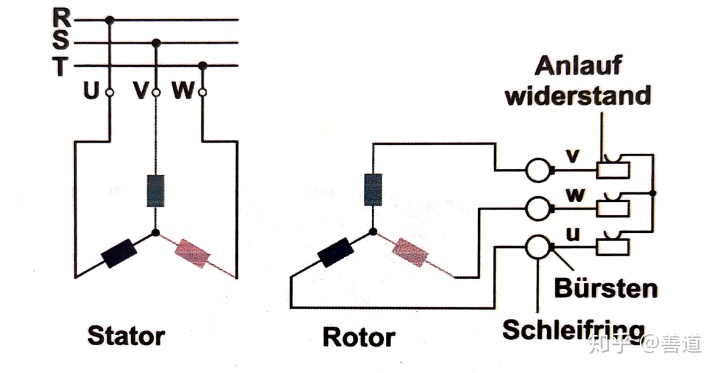
绕线转子电机的带绕线滑环的转子由做出了槽的叠片铁芯构成，并且上面加了和定子绕组类似的三相绕组。其中，槽中的绕组(Drehstromwicklung in Nuten)也像定子绕组一样有相区，经过绕线后，在输出轴另一端接出三捆绕组，分别接上三个同轴的滑环(Schleifringe)，这三个滑环上有电刷(Brüsten)接触，电刷接出后三条支路可接成星形电路。这样就允许外接电阻接上转子电路(比如起动电阻(Anfahrwiderstände))，或者允许直接在转子端通入三相电流。

1.2绕线转子电机的基本原理

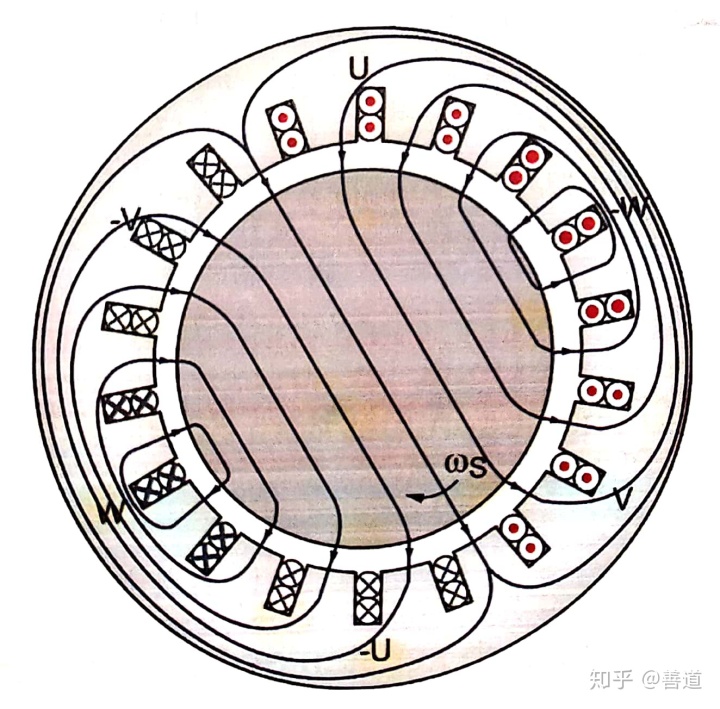
绕线转子电机的定子绕组里通入三相交流电，会产生旋转磁场，如同《德国人怎么学电机——浅谈电机模型(八)：三相交流电机的旋转磁场理论(一)旋转磁动势》里面所提到的一样。通入交流电频率为

，那么产生的旋转磁场的电角速度为 ，机械角速度为 ， 为同步转数

(11.1)

在绕线转子电机的转子中就会产生感应电压，而按照之前旋转磁场理论中所述，三相交流电机的定子在转子上产生的感应电压幅值大小会正比于转差率

以及定子电角速度 。当转子以和同步转数一样的速度运动时，它与定子的旋转磁场相对静止，那么通过转子总磁链就恒定了。按照法拉第电磁感应定理，磁链不时变就无法产生感应电压！即当转差率 ，转子绕组上才会出现感应电压。只考虑基波的影响时，有

(11.2)

在转子上产生的转差频率

(Schlupfkreisfrequenz)

(11.3)

(11.4)

有了转差频率的转子，在转子才会感应出电压。从而在转子绕组上就产生了感应电流，即有了转子的旋转磁动势。转子的旋转磁动势相对于转子，在空间上也是以一个转差角速度

运动

(11.5)

(11.6)

所以在一个异步电机里一共有三个速度，定子的旋转磁场转速

，转子的机械转速 以及转差角速度 。而必须满足旋转磁场理论中的频率条件，电机才可以产生一个恒定的输出转矩。如此，异步电机要产生恒定转矩，转子转数也必须满足频率条件，那么必须不能为同步转数，这也是异步电机(Asynchromaschine)名字的由来。

根据楞次定理，激发出来的感应电流势必阻碍产生它的原因。它会在定子的旋转磁场中产生一个转矩，这个转矩会驱动或者阻碍转子，当有异步转数

时

(11.7)

实际工作时，异步转数总达不到同步转数，有一定转差率，否则就没有感应作用，也没有转矩产生。按照《德国人怎么学电机——浅谈电机模型(十)：三相交流电机的旋转磁场理论(三)旋转磁场和转矩》，转矩大小和定子磁场以及转子磁动势幅值和相位差有关

(11.8)

其中在绕线转子中，一些变量都可以通过转子电路附加的变电阻来影响以及控制。这样传统的会增加额外损耗的电机控制方法在今天往往通过变频电路(Umrichter)来替代。

---

2.绕线转子电机电压方程

通过旋转磁场理论，我们现在可以考察绕线转子电机的稳态工作时的电压方程了。

先做一些基本假设：通过合适方法(分布绕组，短距绕组)，使得高次谐波被削弱很多直至基波允许受限。剩余的假设如下：

定子绕组有 对极对，每极每线圈束的匝数为 ，做了最终能产生绕组因数 的分布绕组(槽洞数为 )和短距绕组(短距比 )布置，定子每捆线圈绕组总电阻为 。转子绕组有 对极对，每极每线圈束的匝数为 ，做了最终能产生绕组因数 的布置，转子和定子叠片都没被倾斜过。转子每捆线圈绕组总电阻为 。
并且在铁芯部分的磁场场强 可以被忽略不计,并且气隙磁场是被假设为中心辐散的。且气隙宽度 保持不变。

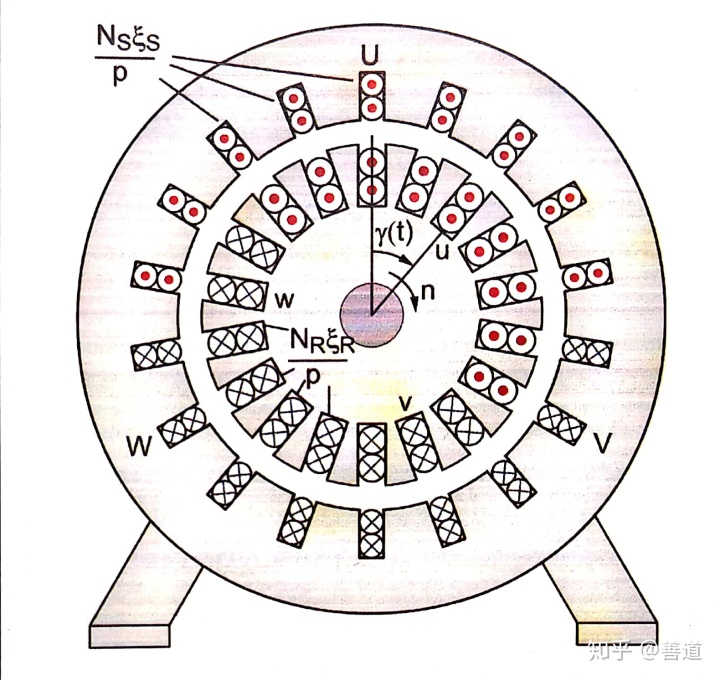
为了探究定子相对于转子的具体相对运动情况，我们有一个合理的简化模型：运动线圈模型。

沿截面展开转子和定子后，定子线圈就在下面图11.5上方定子(Stator)里，以定子线圈为初始位置定下坐标系。线圈宽度为

。第一个转子线圈相对于定子线圈角度 ，第二个相对角度 ，第三个 .显然转子上各个线圈之间相差角度 。那么。定子和转子合成磁场相对于定子的旋转频率为 ，转子本身的旋转频率为 ，则定子和转子合成旋转磁场相对于转子的旋转频率为 。设初始角 ，在第k个线圈束上的相对于起始点的角度

(11.9)

(11.10)

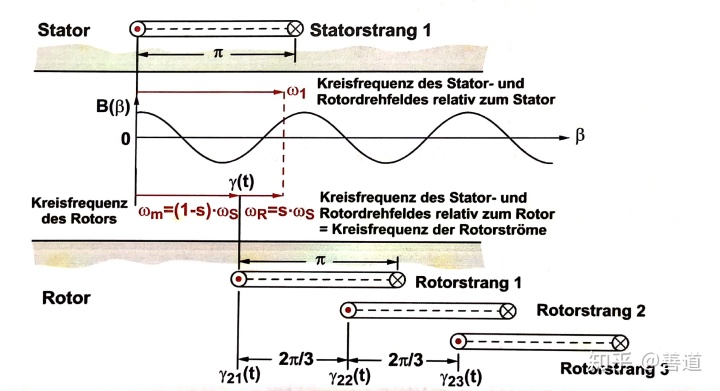
通入定子电流到每个定子线圈束

(U,V,W)，有

(11.11)

转子与定子相差角度

，对应的转子电流为

(11.12)

定子的磁动势为

(11.13)

在定子坐标系下，转子上的磁动势为

(11.14)

最终合成的磁动势为

(11.15)

从定子产生的旋转磁场为

(11.16)

在定子坐标系下，转子上的旋转磁场为

(11.17)

合成场为

(11.18)

有了磁通密度就可以计算磁链，第k个定子线圈束产生的磁链为

(11.19)

在第k个转子线圈束上产生了磁链

(11.20)

在第k个定子线圈束上产生的磁链包含了定子产生的磁链

，以及转子产生的磁链 ，因此我们也可以换一种写法，

(11.21)

同理，在第k个转子线圈束上产生的磁链包含了转子产生的磁链

，以及定子产生的磁链 ，

(11.22)

其中，

为定子的主要自感系数， 为在定子上的互感系数， 为转子的主要自感系数， 为在转子上的互感系数。

(11.23)

(11.24)

(11.25)

实际上除了直接透过气隙到达定子或者转子上的磁通，也存在一些漏磁(Streufelder)。而在绕线槽以及接线头附近的漏磁产生的影响仍是不可忽略的。为了计算这些漏磁，会把漏磁分成槽漏磁(Nutstreufelder)、绕组头端漏磁(Stirnstreufelder)以及气隙漏磁(Luftspaltstreufelder)。其中，气隙漏磁会有定子转子耦合的漏磁或者说高次谐波的漏磁。

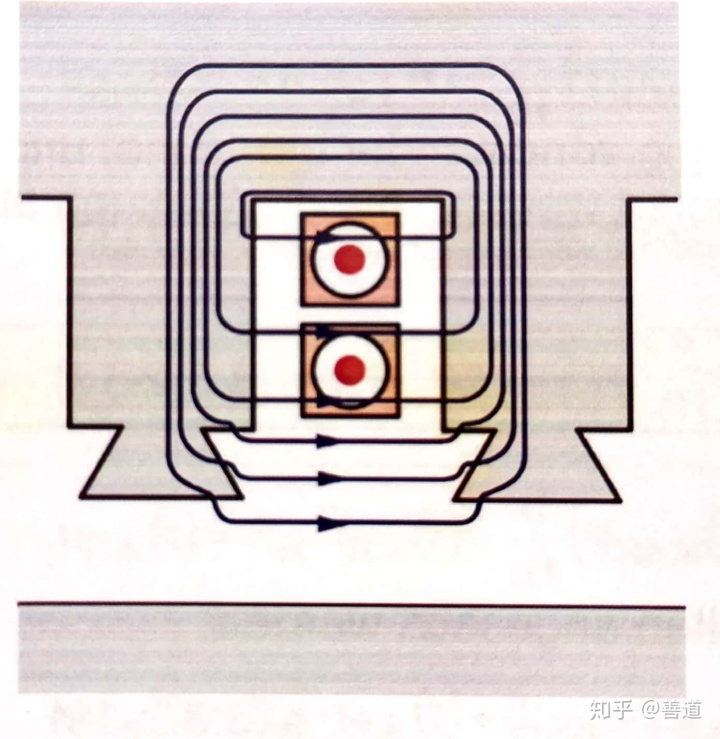
在绕组头(Wickelköpfe)处的定子电流激发的磁场只会部分地和转子的磁场耦合，绝大多数都是自感激发。于是，可以认为绕组头漏磁只是定子主磁场的一点点多余的部分，这样就能画出绕组头漏磁场的替代场，如下图右边

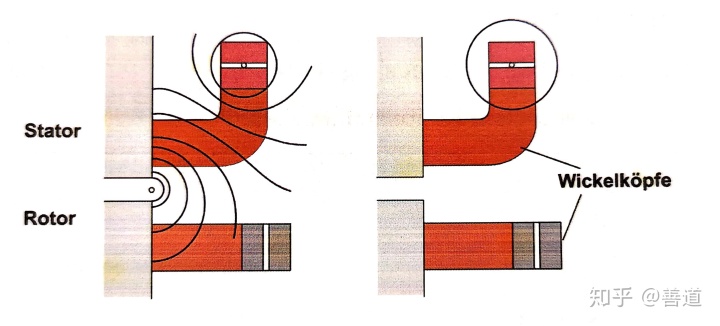
气隙漏磁场可以从旋转磁场的高次谐波中算得。这样可知气隙磁场其中的切向部分就是气隙漏磁场了。

所有漏磁部分均能够单独计算出来，然后叠加算出总的漏磁感应系数

，当我们把所有线圈绕组上的漏磁都考虑进来就可以写出

(11.26)

其中

为槽漏磁部分， 为绕组头端漏磁部分， 为高次谐波漏磁，即气隙漏磁部分。可以认为，所有漏磁磁链都是线性变化的，那么定子漏磁磁链 ，转子漏磁为

(11.27)

(11.28)

定子和转子之间耦合的磁场衍生出的电压变化，就如同变压器主线圈和副线圈之间的变压输电，选择消耗型箭头系统(Verbraucherzählpfeilsystem)，简写为VZS，即所谓的“被动符号规定”，使用感应定律得电路的电压方程

(11.29)

(11.30)

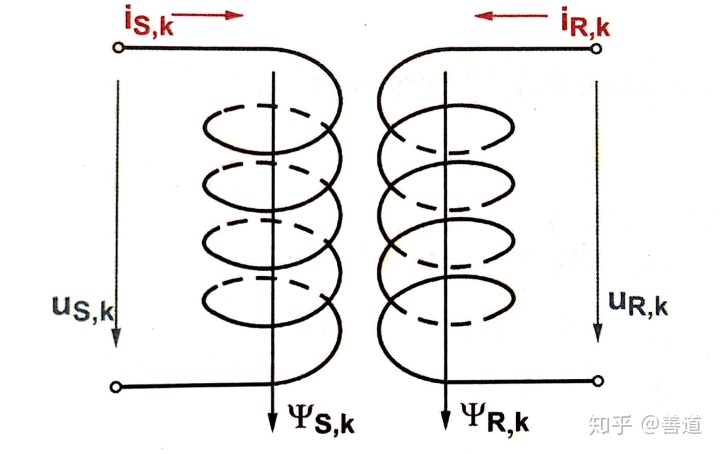
移项后可得针对转子定子各三捆线圈束的总计六个电压方程

(11.31)

(11.32)

其中定子主磁链对应的感应电压

(11.33)

定子的漏磁部分对应的感应电压

(11.34)

定子上源自转子的互感电压

(11.35)

同理，有转子上的主磁链对应的感应电压

(11.36)

转子的漏磁部分对应的感应电压

(11.37)

转子上源自定子的互感电压

(11.38)

显然，以上六个式子完全展开会变得十分繁琐，而且有很多冗余项，冗余的原因是来自三相系统的对称性和可交换性。我们可以使用一种非常巧妙的方法，就可以轻松地用简易方法表示这些式子。那就是在《德国人怎么学电机——浅谈电机模型(七)：交流电机概述》里面提到过的相量法。使用复数来表示这些会旋转的量。

在对称的三相交流系统的稳态工作状态时，其实只用一相就可以表示了，因为当三个相量旋转时，另外两相和这一相分别始终保持120°的相位差。我们直接使用复数相量

来表示一个定子线圈束的量的幅值，根据欧拉公式，余弦值 相当于取了单位复数 的实部，而正弦值 相当于取了复数虚部，则有如下表达

(11.39)

对应的转子线圈束的量

(11.40)

所以定子相量以定子磁场角速度

旋转，转子相量以转子磁场角速度 旋转。

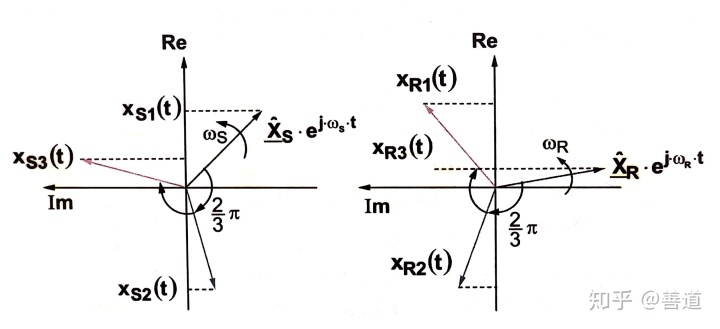
从而之前的电压方程可以改写为

(11.41)

(11.42)

在恒定的供电频率

下，往往直接采用电抗(Reaktanzen)而非自感来表示，这样又可以进一步简化方程。总的定子电抗 ，转子电抗 以及互耦电抗 为

(11.43)

(11.44)

(11.45)

再根据转差率关系

继续简化为

(11.46)

(11.47)

---

3.绕线转子电机的等效替代电路图

根据上述最简式的电压方程可以画出绕线转子电机的等效替代电路图。值得注意的是，定子会在转子中激发频率为

的交变磁场，反过来，转子会在定子中激发频率为 的交变磁场。

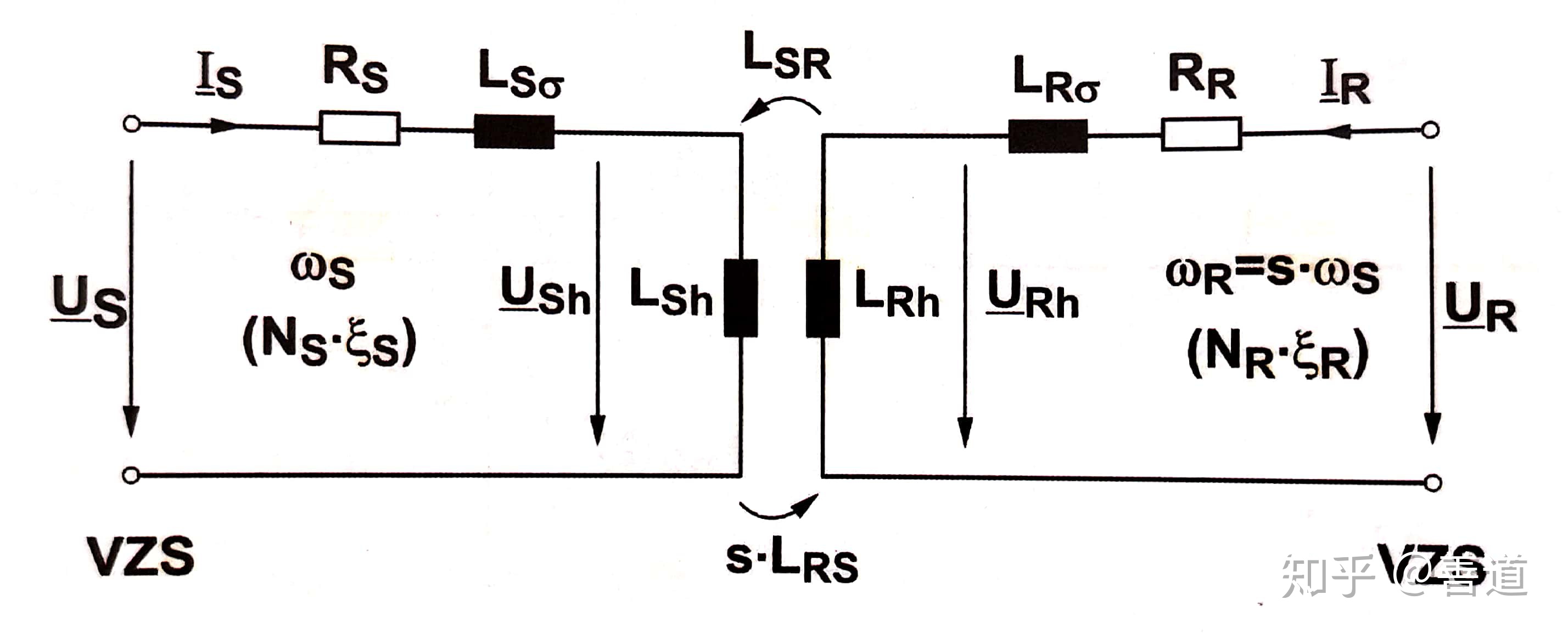
注意到，由于定子和转子之间的电气隔离(galvanische Trennung)，两个电路无法合并到一起。为了能够顺利把两个电路合二为一，我们需要将转子侧的量都换算到定子去。此处可以继续使用变压器的等效模型，根据功率不变的变换，选取一个变换因数

，则有

(11.48)

带“‘“的量均为变换过以后的量，

指的是所有转子上的自感。那么可以获得变换后的关系方程

(11.49)

(11.50)

对于变换因数的选择其实不唯一，它们将导向各不相同的等效替代电路图。通常会有三个不同的等效替代电路图。易知，变换因数还有以下这种关系

(11.51)

(11.52)

(11.53)

(11.54)

(11.55)

现在继续定义漏磁数 (

, )和漏磁系数 (总漏磁数)

(11.56)

为了简化变换过后的电压方程最后的括号里的电流量，引入磁化电流

(Magnetisierungsstrom)，它和 都只是计算中间量，不直接代表物理意义。转子上没有电流的情况下，仍然是定子磁场直接产生合成磁场，而转子电流产生转子磁场。

(11.57)

所以就能得到化简得方程，和对应的一个相的异步电机的T型等效替代电路图

(11.58)

(11.59)

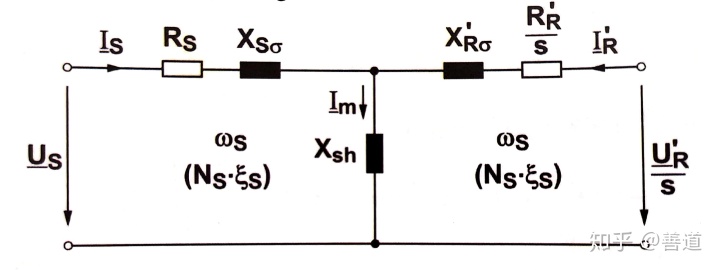
经过变换以后的转子相量就可以和定子的相量进行运算。同时我们也可以画出电机处于各个工作状态下对应的相量图，并且规定定子电压落在实轴正半轴上，以此为参考基准，依照公式所表达的运算关系，画出其他相量和它的关系。

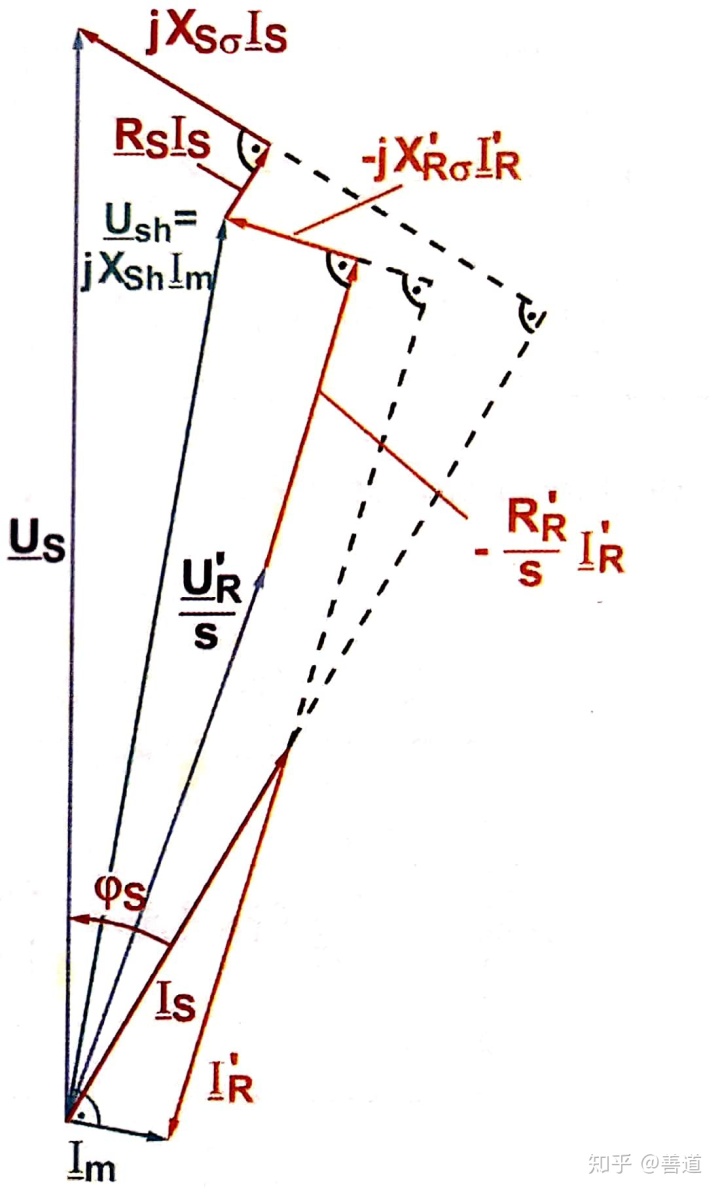
我们刚刚选的变换因数也可以重新选择，使得转子侧的漏磁电抗完全消失。即所谓的“反Gamma变换”(Gamma-invers)。令

有

(11.60)

于是就会有了新的电路参数

(11.61)

(11.62)

(11.63)

新的磁化电流和变换后的转子电流为

(11.64)

所以反Gamma变换下的电压方程为

(11.65)

(11.66)

对应的

-等效替代电路图

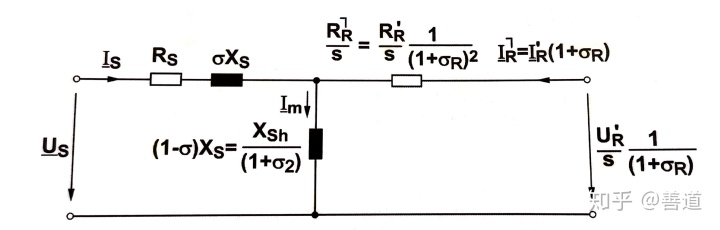
若想要在定子侧的漏磁电抗完全消失则会得到“Gamma变换”。需要

(11.67)

(11.68)

(11.69)

(11.70)

(11.71)

(11.72)

于是有Gamma变换下的电压方程以及对应的

-等效替代电路图

(11.73)

(11.74)

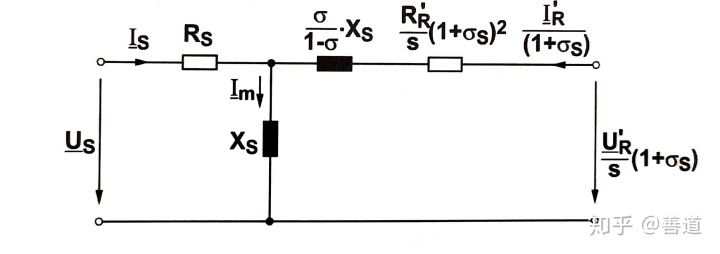
到目前为止，自感强度和电阻都被假设为不变。自感强度会由于电流变化而变化，电阻也会由于温度变化而变化，而且在鼠笼异步电机里面还有电流的集肤效应。而且在推导过程中，位于铁芯中被忽略的磁压，磁动势等，都对有效气隙有影响。

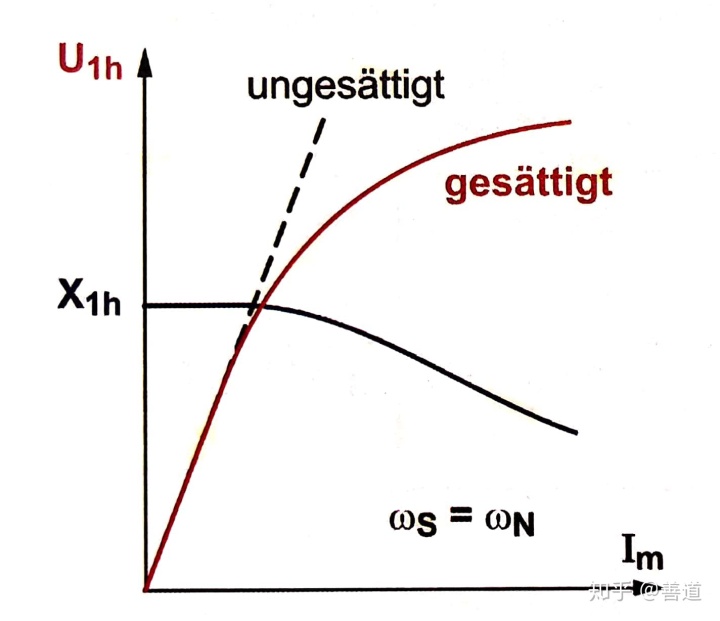
真实场景一般是在等效替代电路图中追加一个并联于主要定子电抗

的铁损电阻 后(自然地，电阻实际大小取决于工作点)，把产生的铁损忽略。

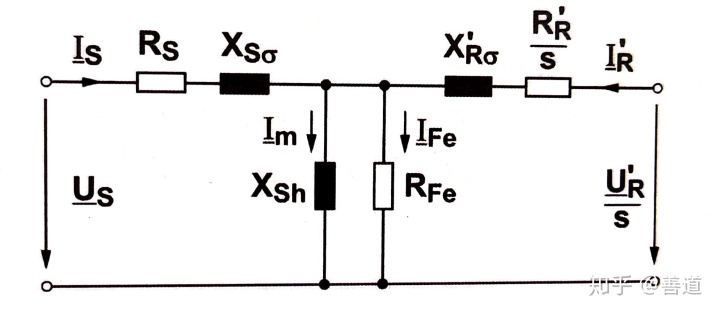
因为磁钢的磁饱和，就会导致磁化电流

和定子感应电压 直接的非线性关系。不过一般地，随着磁化电流增大，电机中不能等比例产生一个更大的磁通，如此一来，定子主电抗 就会下降。而漏磁电抗 以及 本来直到达到额定电流之前也不会和电流强度有关，但是在更高的电流作用下，也会因为漏磁场铁芯路径上的磁饱和，导致它们也随之下降。把槽用槽封楔封闭，则会让这种现象更加明显，即使是比较小的电流。因为槽齿区域已经先一步达到了磁饱和。就如下图所示，红色为实际发生了饱和的非线性的曲线，而黑色虚线为未饱和的直线。

考虑电阻的温升变化，假设金属电阻率

和温度 保持线性关系

(11.75)

所有下标“20”表示处于室温20℃，20℃的铜导线的电阻温度系数

，对于绕组电阻于是就有以下的温度关系

(11.76)

这意味着，如果电机温度提高250K，那么电阻就会是原来的两倍！

4.小结

本章是异步电机的开始，介绍了一下绕线转子电机的基本机械结构和对应的用来描述的电压方程以及等效替代电路图。选取适当变换因数

可以得到不同的简化关系，例如，反Gamma变换和Gamma变换。

下一章将在本篇的基础上继续深入探讨基于相量法的绕线转子电机的电压方程的功率转矩。

下一篇传送门：

善道：德国人怎么学电机——浅谈电机模型(十二)：异步电机：绕线转子电机(二)​zhuanlan.zhihu.com

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！