lingo变量无限制版本_【运筹学】用Lingo求解运输问题，兼谈Lingo语法

一. 运输模型

设有

个产地 其产量（供应量）分别为 ； 个销地 , 其销量（需求量)分别为 ；从产地 运往销地 的运费为 . 假设产销平衡，问如何安排运输方案能使总运费最小？

这就是经典的运输问题，设从

运往 的运量为 (决策变量），则建立产销平衡的运输模型：

其中，约束条件 (1) 表示从

地运出量等于地的供应量；约束条件 (2) 表示运往地的运量等于地的需求量。

若约束 (1) 若改为

, 约束 (2) 仍为 ，则为产大于销的运输模型；

若约束 (2) 若改为

, 约束 (1) 仍为 ，则为销大于产的运输模型。

二. Lingo求解

用Lingo求解，只需要将上述模型按照Lingo语法表示出来，而不用操心任何求解细节。

例 1

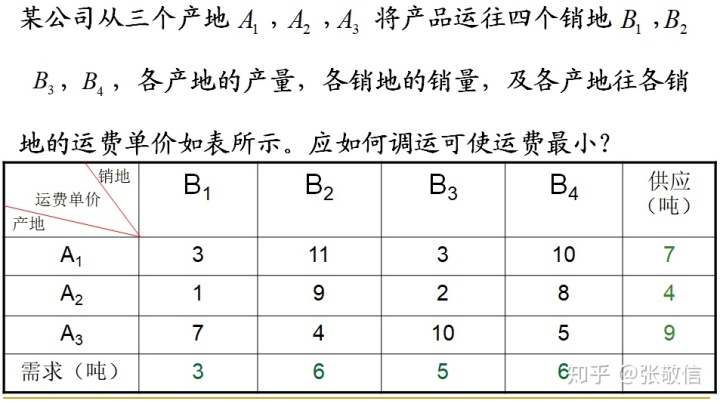
建立运输模型（产销平衡):

其中，运价

供应

，需求 .

Lingo代码:

sets

运行结果（部分）：

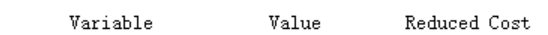
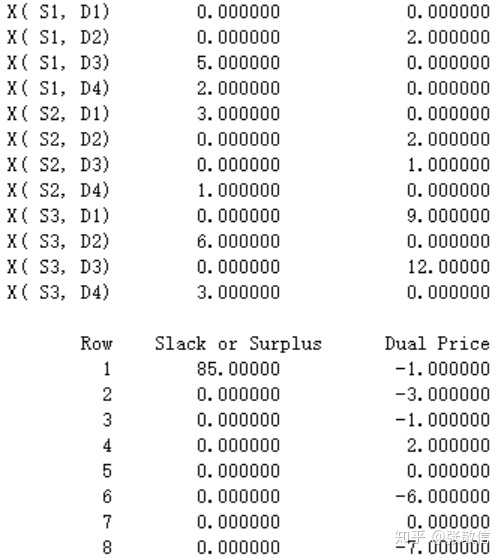
结果解释：最优运费是85，运输方案是：S1往D3、D4分别运送5和2；S2往D1、D4分别运送3和1；S3往D2、D4分别运送6和3.

三. 程序说明

授人予鱼不如授人与渔，所以再讲解一下上面代码涉及到的Lingo语法。

1. Lingo代码段

Lingo代码分为若干片段，比如上面代码包含了：

集合段：sets: ...... endsets ——用来声明和定义数组变量；

数据段：data: ...... enddata ——用数据对变量赋值；

目标与约束段: 即具体模型表述部分（不需起止标志）。

注：另外还可以有初始段和计算段（暂且不谈）。

例 1 涉及到两个一维数据：供应

、需求 ; 以及一个二维数据 . 所以要存储和使用它们，必须要用到集合段和数据段，当然还必须有模型段。

2. 集合段部分

(1) 集合段第一句：supplys /1 .. 3/: S;

声明一个长度为 3 的一维数组 supplys, 并用它定义一个这样的一维数组变量 S.

先是数组名（随便起），再是用两个 / 夹在中间的是数组的下标范围，中间 .. 是省略表示法，接着用 : 定义数组变量 S。

(2) 同理，第二句 demands/1..4/: D; 声明一个长度为 4 的一维数组 demands，并定义一个这样的一维数组变量 D。

(3) 第三句 links(supplys, demands): c, x; 声明一个

的二维数组 links，并用它定义两个这样的二维数组变量 c, x.

把两个一维数组放一起，起个名字叫 links，得到二维数组 links，第1个一维数组的维数就是二维数组的行数维度，第2个一维数组的维数就是二维数组的列数维度。

注意：这里 links 不是Lingo关键字，可以随便起名。

3. 数据段部分

前面定义好的数组变量

，就是为了存放已知数据的，把已知数据赋值给它们，以便目标与约束段使用。

数据中间用 逗号/空格 隔开都可以，二维数据写成一行也行，我这样写比较易读而已。

4. 目标与约束段部分

为什么不叫模型段呢，是因为Lingo一般是把全部代码放在 model: ....... end 中间（就解决一个问题，省略也行），整个叫做模型段。

该部分就是把模型公式“原样”表述出来，咱们对照着来看：

min 

目标函数是求最小，所以用 “min=”

有

，所以需要用到 @sum() 函数， 这是Lingo里的求和函数，首先得告诉它求和的范围， 从1到3， 从1到4，这不正好是前面声明的（对应的）二维数组 links 的大小吗，所以就用 links(i, j)来告诉（也只能用声明的数组来告诉），并用 表示行索引， 表列索引。

然后，冒号，求和里面的表达式。

@for

注意到随着

变化，这实际上是 3 个式子。要表示这种多个重复式子，就用到Lingo里的 @for() 函数，首先得告诉它有多少重复的式子，同样只能用声明的（对应的）数组来告诉，这里是 supplys(i), 并用 表示重复的索引。

关于这种“对应”，有信息提示，比如维数得相同，比如

是从1到3，表示的供应（产地）的下标。

处理完式子的重复，就剩下表示每次的式子了，有

按前面讲到的 @sum() 函数规则来写就行了。

@for

注：上例是产销平衡运输问题，若不是产销平衡，把模型表示部分的代码对应位置的“=”换成“<" 即可（Lingo中 ”<“就是“<=”）。

————————————————————

原创作品，转载请注明，禁止出版盗用。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！