首先，线性和非线性函数之间的区别：

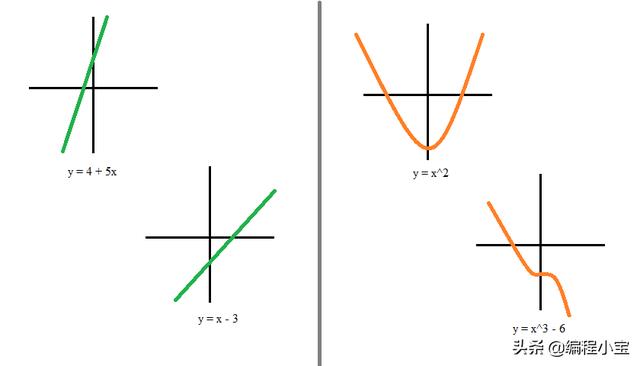
(左)线性函数(右)非线性函数

线性函数:可以简单定义为始终遵循以下原则的函数:

输入/输出=常数。

线性方程总是1次多项式(例如x+2y+3=0)。在二维情况下，它们总是形成直线;在其他维度中，它们也可以形成平面、点或超平面。它们的“形状”总是笔直的，没有任何曲线。这就是为什么我们叫它们线性方程。

非线性函数：即函数图像不是一条直线的函数。高阶多项式是非线性的。三角函数(如sin或cos)是非线性的。平方根是非线性的。

我们如何找到机器学习数据集是否是线性呢？如果我们只有一个维度，那么图形很简单，但是如何处理多维机器学习数据集呢?

生成一个线性数据集

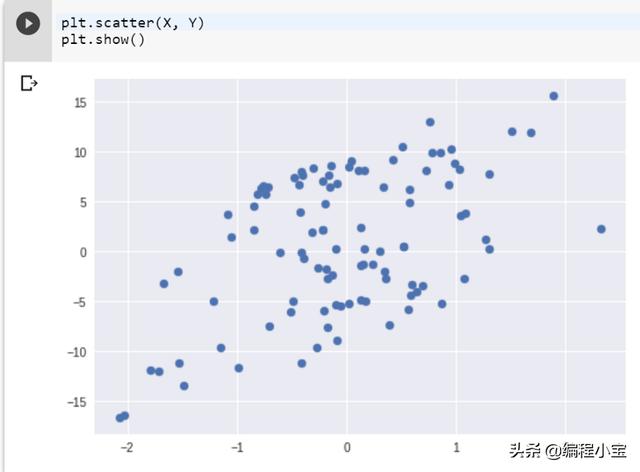
数据集的图形

正如我们在上面的图中所看到的，从图中得到一个函数是否是线性的并不总是那么简单。

问：我们如何解决呢？

因此，我们的想法是将简单的线性回归应用于数据集，然后检查最小平方误差。如果最小平方误差显示高准确度，则意味着机器学习数据集本质上是线性的，否则数据集是非线性的。

好吧，让我们来看看Python代码：

从线性机器学习数据集开始：

# General importsimport numpy as npimport pandas as pdimport matplotlib.pyplot as plt# Generating dataX = np.random.randn(100,1)c = np.random.uniform(-10,10,(100,))# adding another linear columnX = np.hstack((X, 4*X))Y = (4*X[:,1] + c)plt.scatter(X[:, 0], Y)plt.show()plt.scatter(X[:, 1], Y)plt.show()# Applying linear regfrom sklearn.linear_model import LinearRegressionregressor = LinearRegression().fit(X, Y)# Checking the accuracyfrom sklearn.metrics import r2_scoreprint(r2_score(regressor.predict(X), Y))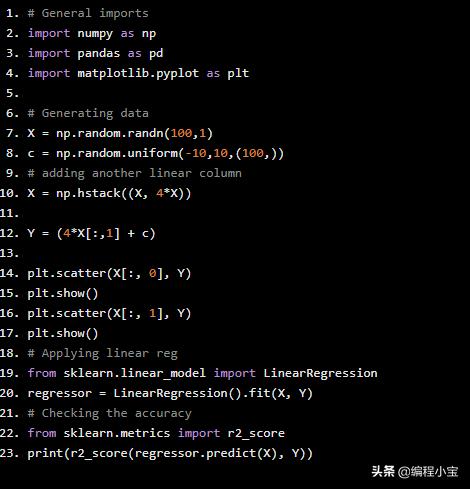

输出：

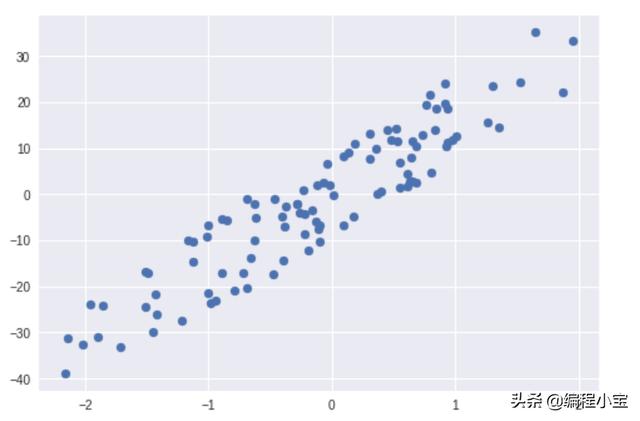
Graph of the first column with y

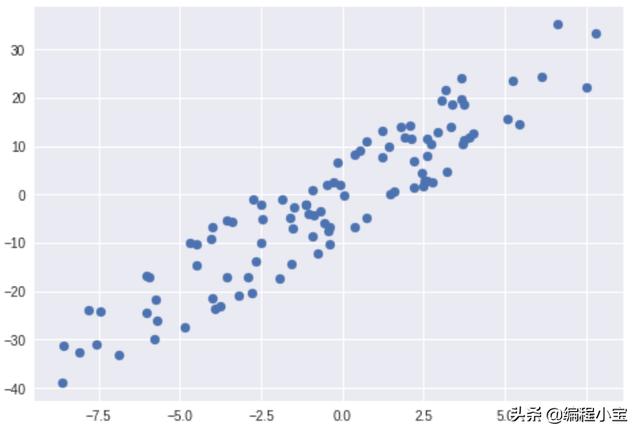
Graph of the second column with y

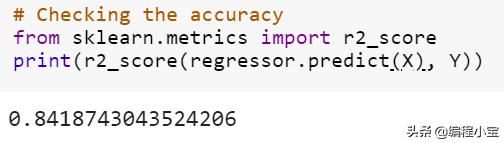
R2准确度得分约为84％

非线性机器学习数据集：

# General importsimport numpy as npimport pandas as pdimport matplotlib.pyplot as plt# Generating dataX = np.random.randn(100,1)c = np.random.uniform(-10,10,(100,))# adding another non-linear columnX = np.hstack((X, X*X))Y = (4*X[:,1] + c)plt.scatter(X[:, 0], Y)plt.show()plt.scatter(X[:, 1], Y)plt.show()# Applying linear regfrom sklearn.linear_model import LinearRegressionregressor = LinearRegression().fit(X, Y)# Checking the accuracyfrom sklearn.metrics import r2_scoreprint(r2_score(regressor.predict(X), Y))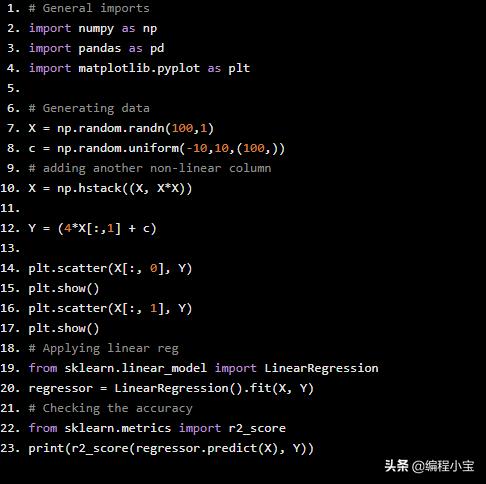

输出：

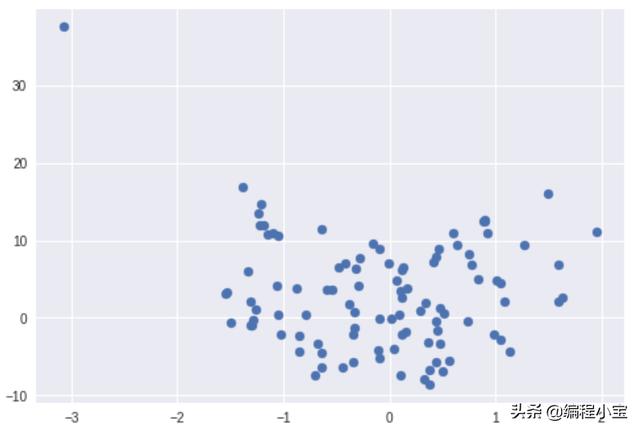
Graph of the first column with y

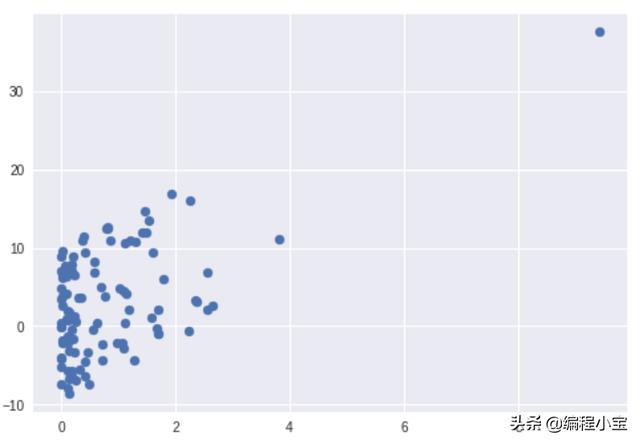
Graph of the second column with y

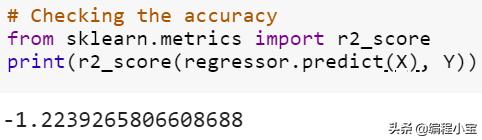
R2准确度得分约为-122％

不用说，这是非常不理想的准确度得分。虽然整个代码几乎相同，但我们可以看到非线性的增加对准确度得分有非常深远的影响。

在开始使用机器学习数据集之前，在小型验证集上使用简单Python代码来检查机器学习数据集是否为线性，可以节省大量的时间。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！