GAN：如何求Discriminator辨别器纳什均衡？（绝对简单，只要懂得基本求导）

本文讲讲如何求解GAN（生成对抗）网络中Discriminator的纳什均衡点。

在看GAN相关的理论文章时，经常会被某些表达和理由给卡住。本文试图解决其中一个。

先抛出问题：

1. 在GAN第一篇论文中，说纳什均衡点是D输出总是0.5，这个0.5是怎么得到的？
2. 在一些文章中，有如下图这样的公式，如何理解？：
   

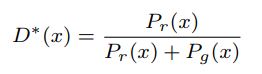
其实，这两个表达比较类似。

以下正文：

先说明将会用到的参数的含义：

1. $x$ 表示输入辨别器Discriminator（以下简称D）的图像，这里不区分是哪里来的；
2. p r ( x ) p_r(x) pr​(x) 表示D对一个真实图像的输出值，这是一个随机变量，不是一个确定的值。这里的$r$表示real；
3. p g ( x ) p_g(x) pg​(x)表示D对一个从生成器Generator（以下简称G）中得到的图像的输出值，也是一个随机变量；
4. $D(x)$表示D对一个输入的输出值；
5. $L(D)$表示D的损失函数。

我们直接假设损失函数$L(D)$已经定义好，形式如下： L ( D ) = ∫ x [ p r ( x ) ∗ l o g ( D ( x ) ) + p g ( x ) ∗ l o g ( 1 − D ( x ) ) ] d x L(D)=\int_x[p_r(x)*log(D(x))+p_g(x)*log(1-D(x))]dx L(D)=∫x​[pr​(x)∗log(D(x))+pg​(x)∗log(1−D(x))]dx
看到这个损失函数相信大家一定熟悉，但却觉得有点不对劲。正常情况下，我们求损失时，我们默认 p r ( x ) p_r(x) pr​(x)就等于1。
公式中的积分实际上是因为我们的随机变量是很多的，不是一个值。这里这样解释恐怕还不是正确的，姑且这样认为吧。

这时我们不继续考虑积分的影响，于是上面的公式变成： L ( D ) = p r ( x ) ∗ l o g ( D ( x ) ) + p g ( x ) ∗ l o g ( 1 − D ( x ) ) L(D)=p_r(x)*log(D(x))+p_g(x)*log(1-D(x)) L(D)=pr​(x)∗log(D(x))+pg​(x)∗log(1−D(x))，这时我们需要求出D的最佳对策，也就是不管你给D输入什么，D都能最大概率是对的。

也就是求上式中$L(D)$的极小值。我们肯定可以直接求导，并令导数等于0即可。

为了简单求导（对$D(x)$求导），我们简化一下上面的参数表示：

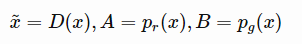
简写可得：

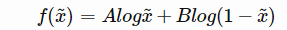
继续求导：

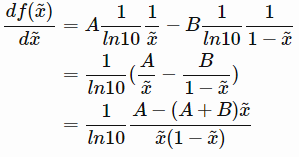
然后我们令导数为0，可得：

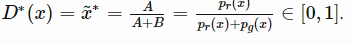
也就是说不管你的输入是什么，我们D最佳的结论就是上面的结果。
举个例子来说，假如你总是给D输入真实的图片，D的最佳结果就是总是输出1，因为这时 p g ( x ) p_g(x) pg​(x)接近于0。反之亦然。

我们假设当G产生的图片和真实图片完全一样时，那么这时 p r ( x ) p_r(x) pr​(x)和 p r ( x ) p_r(x) pr​(x)就相等了，所以D最后只能输出0.5来确保自己在上述那样的损失函数情况下损失最小。

后记：

我们虽然知道纳什均衡是D输出0.5（不管输入什么图片，是真实的，还是合成的），但是我们几乎很难看到真的达到这个均衡点了。

从某种意义上讲，这里的纳什均衡怎样才能达到，还不得而知。

有想法的话，欢迎留言，私信。

参考网址（英文）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！