似然

f(x|θ)表示的就是在给定参数theta的情况下，x出现的可能性多大。L(θ|x)表示的是在给定样本x的时候，哪个参数theta使得x出现的可能性多大。所以其实这个等式要表示的核心意思都是在给一个theta和一个样本x的时候，整个事件发生的可能性多大。

概率和似然等数学对象的区别：

通过了解在某一假设下，已知数据发生的可能性，来评价哪一个假设更接近θ的真实值。似然函数不需要满足归一性。不是所有的可以用0到1之间的数所表示的对象都能称为概率。统计学中的另一常见概念"置信（区间）"(confidence interval)中的置信度(confidence level)也不是概率。更常见的p-值(p-value)严格来说其本身是一个(恰好位于0到1之间的)统计量(即样本随机变量的函数)，所以p-值也不是概率。

一种方便区别是概率还是似然的方法是，根据定义，"谁谁谁的概率"中谁谁谁只能是概率空间中的事件，换句话说，我们只能说，事件(发生)的概率是多少多少(因为事件具有概率结构从而刻画随机性，所以才能谈概率)；而"谁谁谁的似然"中的谁谁谁只能是参数。

似然函数

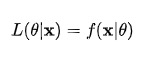
概率(密度)表达给定theta下样本随机向量X=x的可能性，而似然表达了给定样本X=x下参数theta1(相对于另外的参数theta2)为真实值的可能性。我们总是对随机变量的取值谈概率，而在非贝叶斯统计的角度下，参数是一个实数而非随机变量，所以我们一般不谈一个参数的概率。

回到似然函数表达式。首先我们严格记号，竖线｜表示条件概率或者条件分布，分号；表示把参数隔开。所以这个式子的严格书写方式是

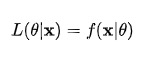
应写为

因为右端的theta只能当作参数理解。

极大似然估计参考 CSDN博客

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！