《算法》练习题1.1.1--1.1.39 答案解析
文章目录
- 0.0.0
- 1.1.1
- 1.1.2
- 1.1.3
- 1.1.4
- 1.1.5
- 1.1.6
- 1.1.7
- 1.1.8
- 1.1.9
- 1.1.10
- 1.1.11
- 1.1.12
- 1.1.13
- 1.1.14
- 1.1.15
- 1.1.16
- 1.1.17
- 1.1.18
- 1.1.19
- 1.1.20
- 1.1.21
- 1.1.22
- 1.1.23
- 1.1.24
- 1.1.26
- 1.1.27
- 1.1.28
- 1.1.29
- 1.1.30
- 1.1.31
- 1.1.32
- 1.1.33
- 1.1.35
- 1.1.36
- 1.1.37
- 1.1.38
- 1.1.39
0.0.0
答案解析代码在我的github:BitHachi/Algorithm-Four
本篇文章已同步到:https://www.bithachi.cn/posts/801dfee5.html
1.1.1


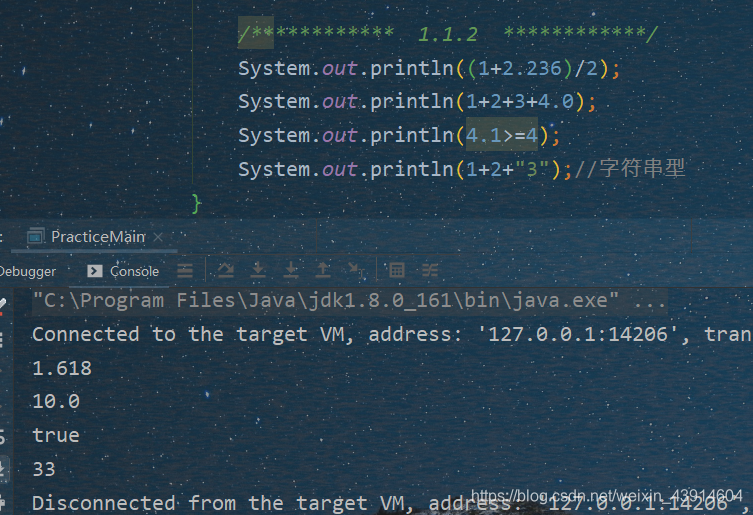
1.1.2

1.1.3


1.1.4

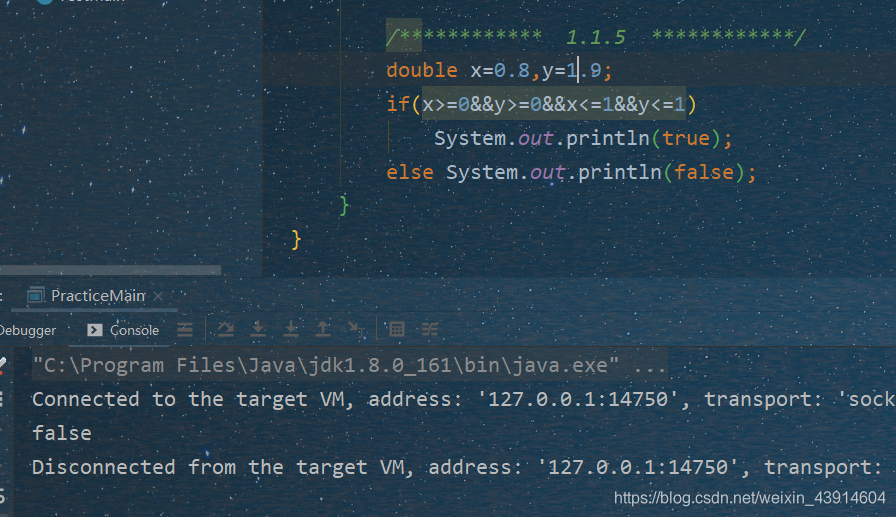
1.1.5
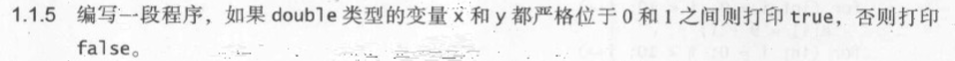
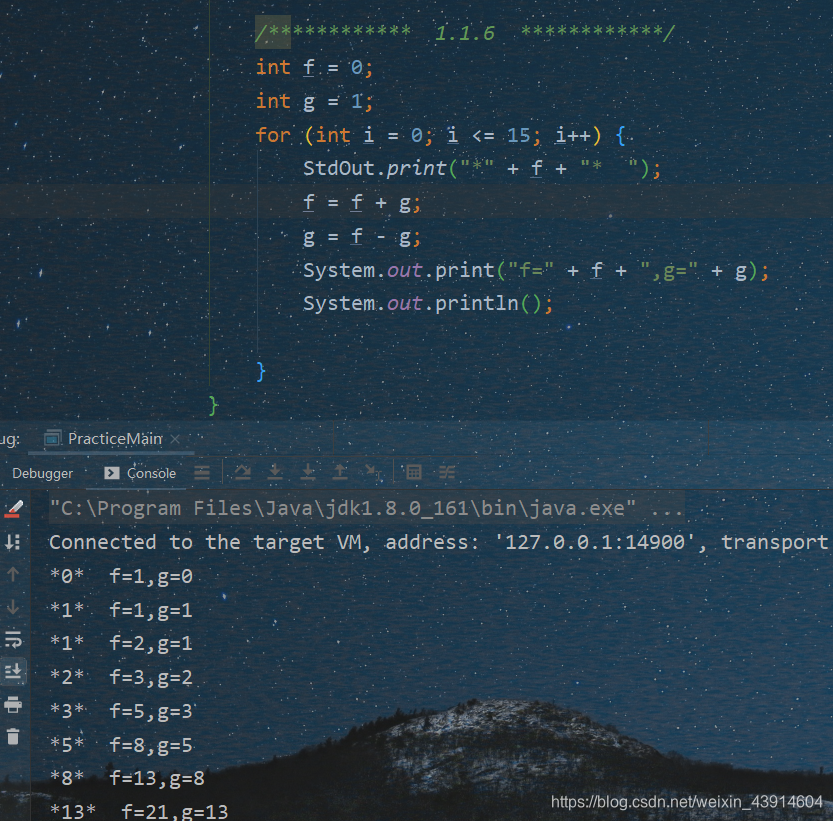
1.1.6

1.1.7


1.1.8


1.1.9


1.1.10


1.1.11


1.1.12


1.1.13
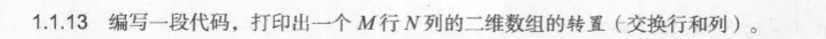



1.1.14
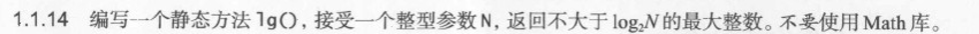

1.1.15



1.1.16
给出exR1(6)的返回值


1.1.17
见书,书上有解析
1.1.18


1.1.19
public class Fibonacci{public static long F(int N){if (N==0) return 0;if (N==1) return 1;return f(N-1)+F(N-2);}public static void main(String[] args){for(int N=0;N<100;N++)StdOut.println(N+" "+F(N));}
}
开发F(N),用数组保存已经计算过的值。

1.1.20
编写一个递归的静态方法计算ln(N!)的值。

1.1.21
编写一段程序,从标准输入按行读取数据,其中每行都包含一个名字和两个整数。然后用printf()打印一张表格,每行的若干列数据包括名字、两个整数和第一个整数除以第二个整数的结果,精确到保留小数点后三位。

1.1.22
使用1.1.6.4节中的rank(递归方法重新实现BinarySearch并跟踪该方法的调用。每当该方法被调用时,打印出它的参数1o和hi并按照递归的深度缩进。提示:为递归方法添加一个参数来保存递归的深度。
1.1.23
为BinarySearch的测试用例添加一个参数:
+ 打印出标准输人中不在白名单上的值;
-则打印出标准输人中在白名单上的值。

1.1.24
- 给出使用欧几里德算法计算105和24的最大公约数的过程中得到的一系列p 和q的值。
- 扩展该算法中的代码得到一个程序Euclid, 从命令行接受两个参数,计算它们的最大公约数并打印出每次调用递归方法时的两个参数。
- 使用你的程序计算111 111和1 234 567的最大公约数。


1.1.26
将三个数字排序。假设a,b,c和t都是同一种原始数字类型的变量。证明以下代码能够将a,b,c按照升序排列。

1.1.27
二项分布。 估计用以下代码计算binomial(100,50,0.25)将会产生的递归调用次数。
将已经计算过的值保存在数组中并给出一个更好的实现。



1.1.28
删除重复元素。 修改BinarySearch类中的测试用例来删去排序后白名单中的所有元素。

1.1.29
等值键。为BinarySearch类添加一个静态方法rank(),它接受一个键和一个整型有序数组(可能存在重复键)作为参数并返回数组中小于该键的元素数量,以及一个类似的方法count()来返回数组中等于该键的元素的数量。
注意:如果i和j分别是rank(key,a)和count(key ,a)的返回值,那么a[i…i+j-1]就是数组中所有和key相等的元素。

1.1.30
数组练习。编写一段程序,创建一个NxN的布尔数组a[][]。其中当i和j互质时(没有相同因子),a[i][j] 为true,否则为false。


1.1.31
随机连接。编写一段程序,从命令行接受一个整数N和double值p (0到1之间)作为参数,在一个圆上画出大小为0.05且间距相等的N个点,然后将每对点按照概率p用灰线连接。


1.1.32
直方图。假设标准输人流中含有一系列double值。编写-段程序, 从命令行接受一个整数 N和两个double值l和r。将(I, r)分为N段并使用StdDraw画出输人流中的值落人每段的数量的直方图。


1.1.33





1.1.35
模拟掷骰子。以下代码能够计算每种两个骰子之和的准确概率分布:
int SIDES = 6;
double[] dist = new double[2 * SIDES + 1];
for(int i = 1; i <= SIDES; i++)for(int j = 1; j <= SIDES; j++)dist[i+j] += 1.0;
for (int k = 2; k <= 2*SIDES; k++)dist[k] /= 36.0;
dist[i] 的值就是两个骰子之和为i 的概率。用实验模拟N 次掷骰子,并在计算两个1 到 6 之间的随机整数之和时记录每个值的出现频率以验证它们的概率。N 要多大才能够保证你的经验数据和准确数据的吻合程度达到小数点后三位?




1.1.36
乱序检查。通过实验检查表1.1.10中乱序代码是否能够产生预期的效果。编写一个程序ShuffleTest,接受命令行参数M和N,将大小为M的数组打乱N次且每次打乱之前都将数组重新初始化为a[i]=i.打印一个MXM的表格,对于所有的列j,行i表示的是i在打乱后落到j的位置的次数。数组中的所有元素的值都应该接近于N/M。
package Chapter1.Section11;import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.StdRandom;/**
* @Program: Algorithm
* @ClassName: EX36
* @Author: Mr.BitHachi
* @CreateTime: 2020-07-16 19:11
* @Version: V1.0
* @Description: 练习题1.1.36
*
* 参考:https://www.cnblogs.com/longjin2018/p/9848742.html
**/public class EX36 {public static void main(String[] args){
// int M=Integer.parseInt(args[0]);
// int N=Integer.parseInt(args[1]);int M=6,N=10;int[] a=new int[M];int[][] Info=new int[M][M];//N次打乱for(int k=0;k<N;k++){//每次打乱前数组重新初始化为a[i]=ifor(int i=0;i<M;i++)a[i]=i;//打乱shuffle(a);//打乱后i行的值落到j列的次数增1for(int i=0;i<a.length;i++)Info[a[i]][i]++;}//打印M*M数组printArray(Info);}//打乱数组public static void shuffle(int[] a){int N=a.length;for (int i=0;i<N;i++){int r=i+ StdRandom.uniform(N-i);//返回0~N-i之间的整数再加iint temp=a[i];a[i]=a[r];a[r]=temp;}}//结束打乱//打印数组private static void printArray(int[][] array){int rowLen=array.length;int colLen=array[0].length;StdOut.printf(" ");for (int col=0;col<colLen;col++)StdOut.printf("%5d",col);StdOut.printf("\n");//for (int row=0;row<rowLen;row++){StdOut.printf("%d",row);for (int col=0;col<colLen;col++)StdOut.printf("%5d",array[row][col]);StdOut.printf("\n");}}
}1.1.37
糟糕的打乱。假设在我们的乱序代码中你选择的是一个0 到N-1 而非i 到N-1 之间的随机整数。证明得到的结果并非均匀地分布在N! 种可能性之间。用上一题中的测试检验这个版本。
package Chapter1.Section11;import edu.princeton.cs.algs4.StdRandom;/*** @Program: Algorithm* @ClassName: EX37* @Author: Mr.BitHachi* @CreateTime: 2020-07-16 19:23* @Version: V1.0* @Description: 练习题1.1.37**/public class EX37 {public static void shuffle(int[] a) {int N = a.length;for (int i = 0; i < N; i++) {int r = StdRandom.uniform(N); // [0,N)int temp = a[i];a[i] = a[r];a[r] = temp;}}public static void main(String[] args) {
// if (args.length < 2) {
// System.out.println("Error");
// return;
// }
// int M = Integer.parseInt(args[0]), N = Integer.parseInt(args[1]);int M=6,N=10;int[] a = new int[M];int[][] Info=new int[M][M];for(int k=0;k<N;k++){//每次打乱前数组重新初始化为a[i]=ifor(int i=0;i<M;i++)a[i]=i;//打乱shuffle(a);//打乱后i行的值落到j列的次数增1for(int i=0;i<a.length;i++)Info[a[i]][i]++;}for(int []i : Info) {for (int j:i)System.out.print(j + " ");System.out.println();}}
}1.1.38
二分查找与暴力查找。根据1.1.10.4 节给出的暴力查找法编写一个程序bruteForceSearch,在你的计算机上比较它和BinarySearch 处理largeW.txt 和largeT.txt 所需的时间。


1.1.39
随机匹配。编写一个使用BinarySearch 的程序,它从命令行接受一个整型参数T,并会分别针对N=103、104、10^5 和10^6 将以下实验运行 T 遍:生成两个大小为N 的随机6 位正整数数组并找出同时存在于两个数组中的整数的数量。打印一个表格,对于每个N,给出T 次实验中该数量的平均值。
package Chapter1.Section11;import edu.princeton.cs.algs4.StdRandom;import java.util.Arrays;/*** @Program: Algorithm* @ClassName: EX39* @Author: Mr.BitHachi* @CreateTime: 2020-07-16 19:57* @Version: V1.0* @Description: 练习题1.1.39**/public class EX39 {public static void main(String[] args) {
// int T = Integer.parseInt(args[0]);int T=6;int[] num = new int[4];for (int i = 0; i < T; i++) {//对N为10^3 10^4 10^5 10^6运行T遍int N = 100;for (int j = 0; j < 4; j++) {N *= 10; //对N为10^3 10^4 10^5 10^6运行T遍int[] a = new int[N];int[] b = new int[N];for (int k = 0; k < N; k++) {a[k] = StdRandom.uniform(100000, 1000000);//[100000, 1000000)b[k] = StdRandom.uniform(100000, 1000000);}Arrays.sort(a);for (int k = 0; k < N; k++) {//二分循环查找一个数组中的值是否在另一个数组中if (BinarySearch.indexOf(a, b[k]) != -1) {num[j]++; //对于每个N,N为10^3 10^4 10^5 10^6}}}}System.out.println("N\t\tAverage");int N = 100;for (int i = 0; i < 4; i++) {N *= 10;//N为10^3 10^4 10^5 10^6System.out.printf("%d\t%f\n", N, (double) num[i] / T);}}
}参考:
- 《百科》
- 《算法:第四版》课后练习 1.1 答案
- github: https://github.com/jimmysuncpt/Algorithms
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!