Alpha-Beta剪枝算法/极大极小值算法 伪代码,思路与解题流程
伪代码
function alphabeta(node, depth, α, β, maximizingPlayer) isif depth = 0 or node is a terminal node thenreturn the heuristic value of nodeif maximizingPlayer thenvalue := −∞for each child of node dovalue := max(value, alphabeta(child, depth − 1, α, β, FALSE))α := max(α, value)if α ≥ β thenbreak (* β cut-off *)return valueelsevalue := +∞for each child of node dovalue := min(value, alphabeta(child, depth − 1, α, β, TRUE))β := min(β, value)if α ≥ β thenbreak (* α cut-off *)return value
相关定义
α \alpha α代表下界, β \beta β代表上界
解析
在maximum内部,求节点的下界极大值v, v的值被赋给 α \alpha α, α \alpha α 参与区间判断, 若 在 区 间 内 , 则 将 v 返 回 \textcolor{Green}{若在区间内,则将v返回} 若在区间内,则将v返回
在minimum内部,求节点的上界极小值v, v的值被赋给 β \beta β, β \beta β 参与区间判断, 若 在 区 间 内 , 则 将 v 返 回 \textcolor{Green}{若在区间内,则将v返回} 若在区间内,则将v返回
查看伪代码注意到一个问题:
α := max(α, value)
β := min(β, value)
在这两处伪代码: 即便v不会导致 α 或 者 β \alpha或者\beta α或者β的值发生改变,v仍然能够传递出去,这引申出后面的讨论
函数结构:
\qquad 输入参数:
\qquad \qquad 区 间 [ α , β ] , 层 数 / 深 度 \textcolor{Red}{区间[\alpha,\beta],层数/深度} 区间[α,β],层数/深度
\qquad \qquad 区间的作用是确认单独求出的 α \alpha α或者 β \beta β不超出范围.
\qquad 返回值:
\qquad \qquad maximum返回 α \alpha α
\qquad \qquad minimum返回 β \beta β
剪枝流程
这里以流程图来表述
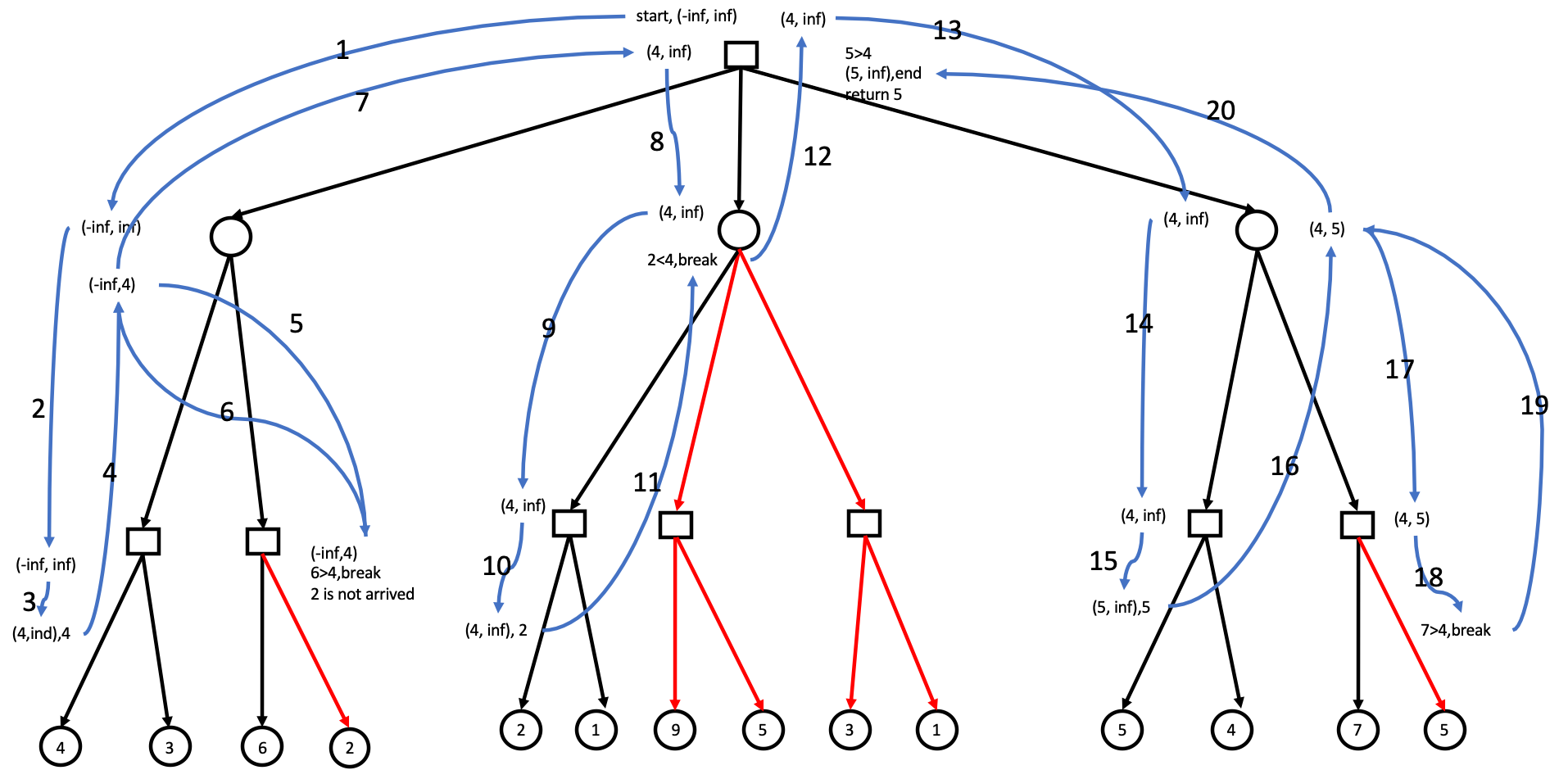
图中 红 线 \textcolor{Red}{红线} 红线代表被剪枝的部分, 蓝 线 \textcolor{Blue}{蓝线} 蓝线代表流程,正方形代表maximum,圆形代表minimum
剪枝算法内部旨在求 α \alpha α的下界极大值, β \beta β的上界极小值
讨 论 \textcolor{Red}{讨论} 讨论:
\qquad 流程5与流程10的差别:
\qquad 在流程5, 经 过 i f α ≥ β t h e n 经过\ if\ \ α ≥ β\ then 经过 if α≥β then 的判断,可以知道数字6直接导致超出区间范围,立刻剪枝,另一分支不再被访问
\qquad 在流程10,区间范围是[4,inf],由于 2 ≤ 4 2\leq 4 2≤4,所以 α \alpha α不发生改变, ∴ 4 ≤ i n f \therefore\textcolor{Red}{4\leq inf} ∴4≤inf,符合范围,v的值被传递出去,传递出去之后,剪枝
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!