递归算法解决梵塔问题

问题简述：

“梵塔问题”源于以下的古老传说：

在世界中心贝那勒斯（印度北部的佛教圣地）的圣庙里，安放着一块黄铜板，板上插著三根细细的、镶上宝石的细针，细针像菜叶般粗，而高就像成人由手腕到肘关节的长。

当印度教的主神梵天在创造地球这个世界时，就在其中的一根针上从下到上放了半径由大到小的六十四片圆金片环，这就是有名的「梵塔」或称「汉内塔」（Towers of Hanoi）。

抽象模型：

已知有三根石柱，不妨设为A,B,C，其中A上套有自下向上依次增大的64个圆盘，问如何将A的圆盘全部转移到B上，移动的规则是：每次只能移动一个圆盘，且不允许将大盘放到小盘上。

考虑递归递归算法，并将问题分解：

（1）先设法将63个圆盘从A移动到C

（2）将A上最后一个盘移动到B

（3）将C上63个盘全部移动到B上

#honoi问题
def honoi(n,first,second,third):if n==1:return print('move a disk'+'  from  ' +first+ '  to  '+ second)honoi(n-1,first,third,second)print ('move a disk'+'  from  ' +first+ '  to  '+ second) honoi(n-1,third,second,first)
honoi(5,'A','B','C')   

显然，n=64时是个无穷数，此处以n=5为例。

执行结果：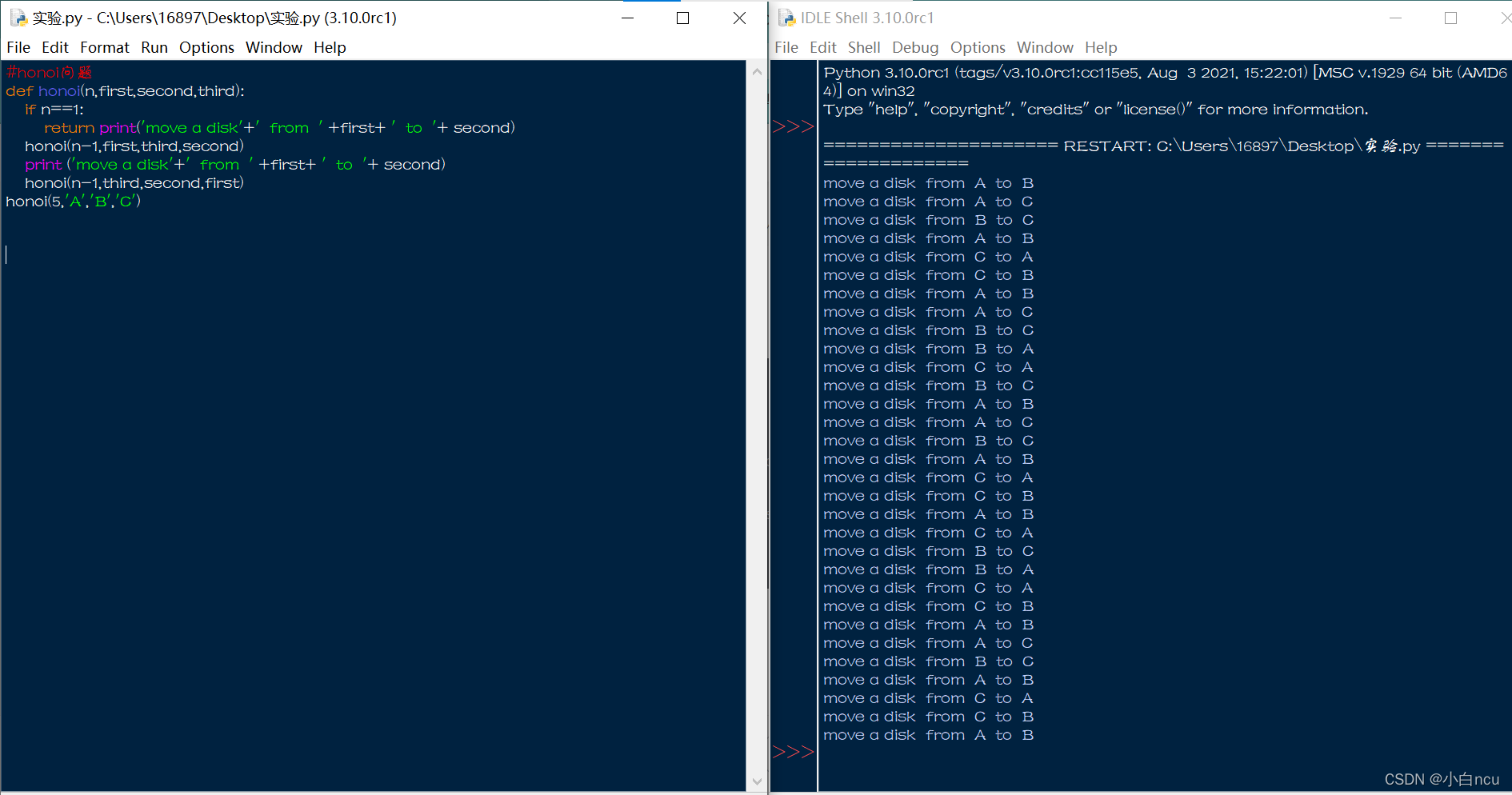

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！