作业辅导视频 SS2023-HW12:从系统框图到系统函数
从系统框图到系统函数
-
信号与系统 2023年春季作业要求与参考答案汇总
-
信号与系统 2023(春季) 作业要求 - 第十二次作业
-
信号与系统 2023(春季) 作业参考答案 - 第十二次作业
01 第十二次作业
一、习题简介
在变换域内研究线性时不变系统, 利用系统函数比较方便。 获得系统的系统函数是关键。 这里给出了常见到的获取系统函数的方法。 根据系统框图建立系统函数是最常见的方法。 在第十二次作业中, 有两个习题, 要求根据给定的系统框图, 求解系统函数, 并在此基础上, 求取系统在给定的激励信号下的零状态输出。 并分析系统的稳定性。 下面让我们来讨论一下求解的思路。

二、习题求解
1、第一小题
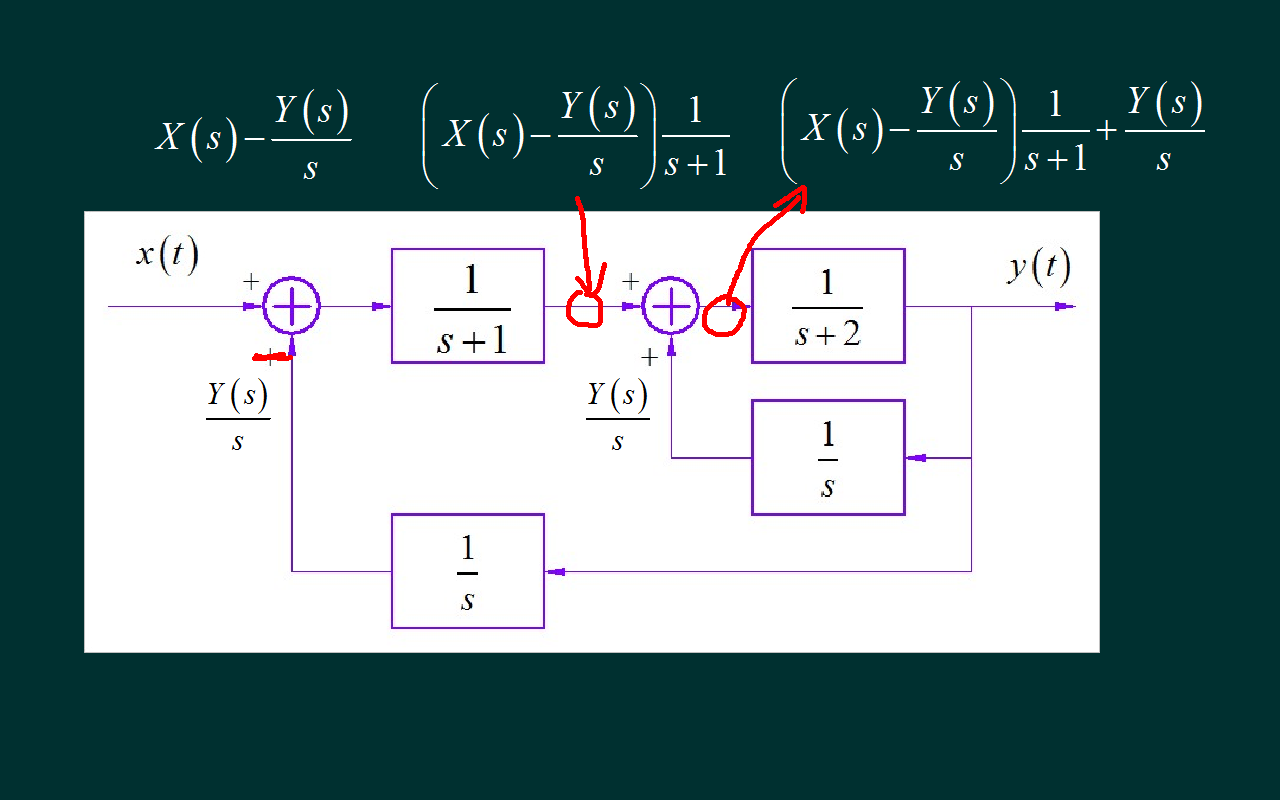
首先, 分析一下第一小题。 这个系统带有两个综合器, 一般情况下可以通过设定临时中间结点变量来求系统的传递函数。 由于这个系统相对比较简单, 下面我们根据各支路连接关系, 逐步写出各个支路的变量。 这是第一个反馈支路。 对应着 s 分之 Y(s)。 第二个反馈支路, 同样也是 s 分之 Y(s)。 那么, 第一个综合器的输出信号 就等于 X(s) 加上 s 分之 Y(s)。 经过第一个前向子系统, 对应的输出等于综合器的输出乘以 s + 1 分之1。 第二个综合器的输出, 将它两个输入信号相加, 便可以得到它的输出。 最后, 通过第二个前向子系统, 等于系统最终的输出信号 Y(s)。 这是我们得到的输入输出之间的方程。

下面整理一下这个代数方程, 消去分母多项式, 将所有的 Y(s) 移动到等号右边, 合并同类项, 便得到X(s), Y(s) 线性方程。 取 Y(s) 除以 X(s) 便得到了系统函数。

习题的第二小问, 是求系统的单位冲激响应。 下面使用因式分解方法 来对系统函数进行 Laplace 反变换, 这样便可以得到系统的单位冲激响应。 这是分解所得到的三个一阶有理分式。 你们也别问怎么得到的。 为了保证分解结果的正确性, 使用了 MATLAB 帮助进行因式分解。 下面, 写出每个因式对应的右边时域信号表达式。 这是一个有三个指数函数的信号。 在单位冲激响应信号中, 包括一个指数增加的分量, 这使得 h(t) 不满足绝对可积。 所以该系统是不稳定系统。 实际上, 系统框图中两个积分反馈都是正向反馈, 也可以定性得到系统不稳定的结论。

实际上, 如果将最外层的反馈, 改成负反馈, 这样整个系统就会变成稳定的。 还是根据前面推导的方式, 得到输入输出之间的表达式。 化简这个表达式。 最终可以得到系统函数。 这个系统函数带有两个极点, 它们都小于零。 所以系统是稳定的。 从这个分析中来看, 原习题系统不稳定的确来自于系统的正向积分反馈所导致的。
2、第二小题
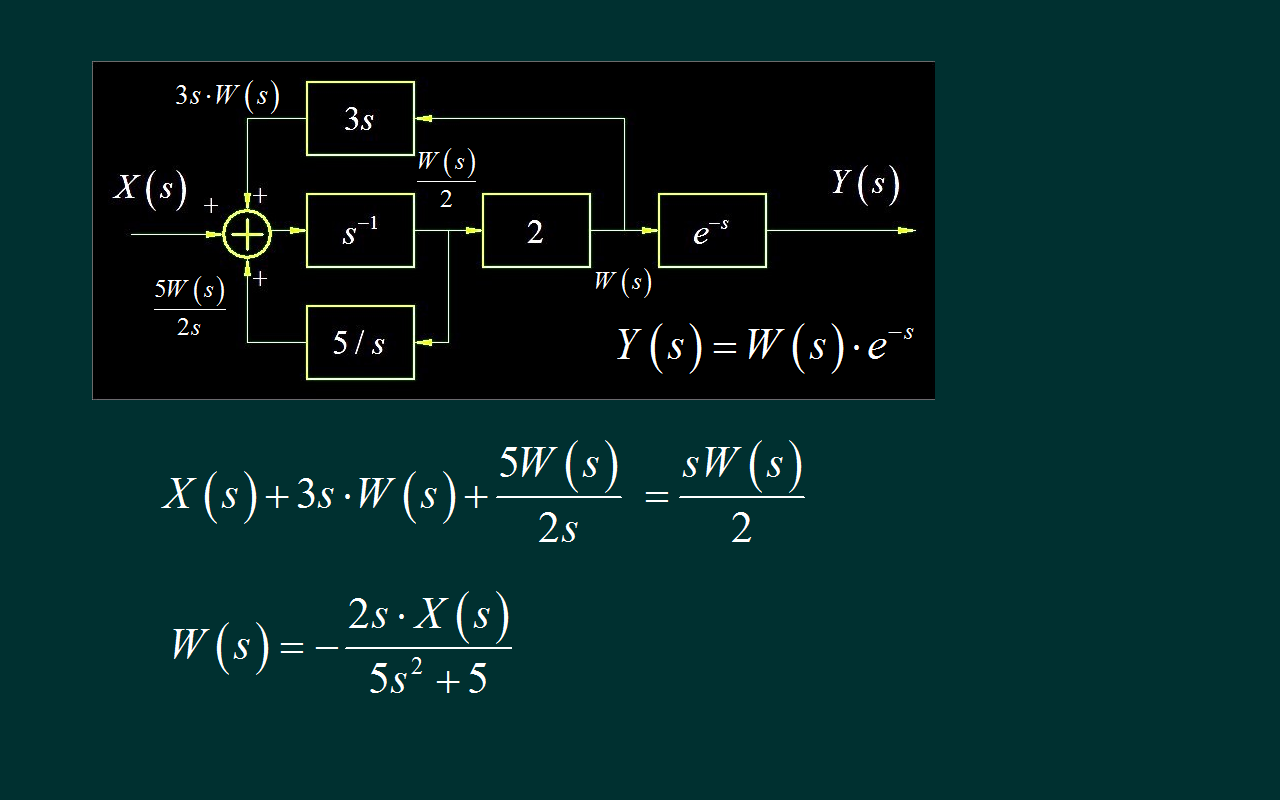
对于第二小题, 为了分析方便, 设置中间变量 W(s)。 根据上面微分反馈, 得到 3s 乘以 W(s)。 根据 比例为 2 的子系统, 可以得到前面支点的变量。 在根据下面的积分反馈, 得到5倍的 W(s) , 除以 2s。 根据综合器, 得到他的输出, 然后在根据后面的积分环节, 输出等于s乘以W(s) 除以2。 下面化简所得到的方程。 可以得到 W(s) 与 X(s) 之间的表达式。 再根据 W(s) 与 Y(s) 之间的延迟关系。 可以写出 Y(s) 的表达式。 将已经得到的 W(s) 的结果代入, 便可以获得 Y(s), X(s) 之间的表达式。 由此,便可以得到系统的传递函数。 这是一个带有纯延迟环节的系统函数。
下面根据系统函数 求解系统的零状态响应。 将输入信号进行Laplace变换。 系统的零状态输出等于输入乘以系统函数, 这是一个带有延迟环节的 Laplace变换。 对于其中有理分式项, 先求取它对应的时域波形表达式, 省去其中的求解环节, 利用 Python进行 Laplace反变换, 得到对应的时域表达式。 再考虑延迟项, 将刚刚求出的信号延迟 1, 便得到系统的实际输出表达式。 这是该系统的零状态响应。
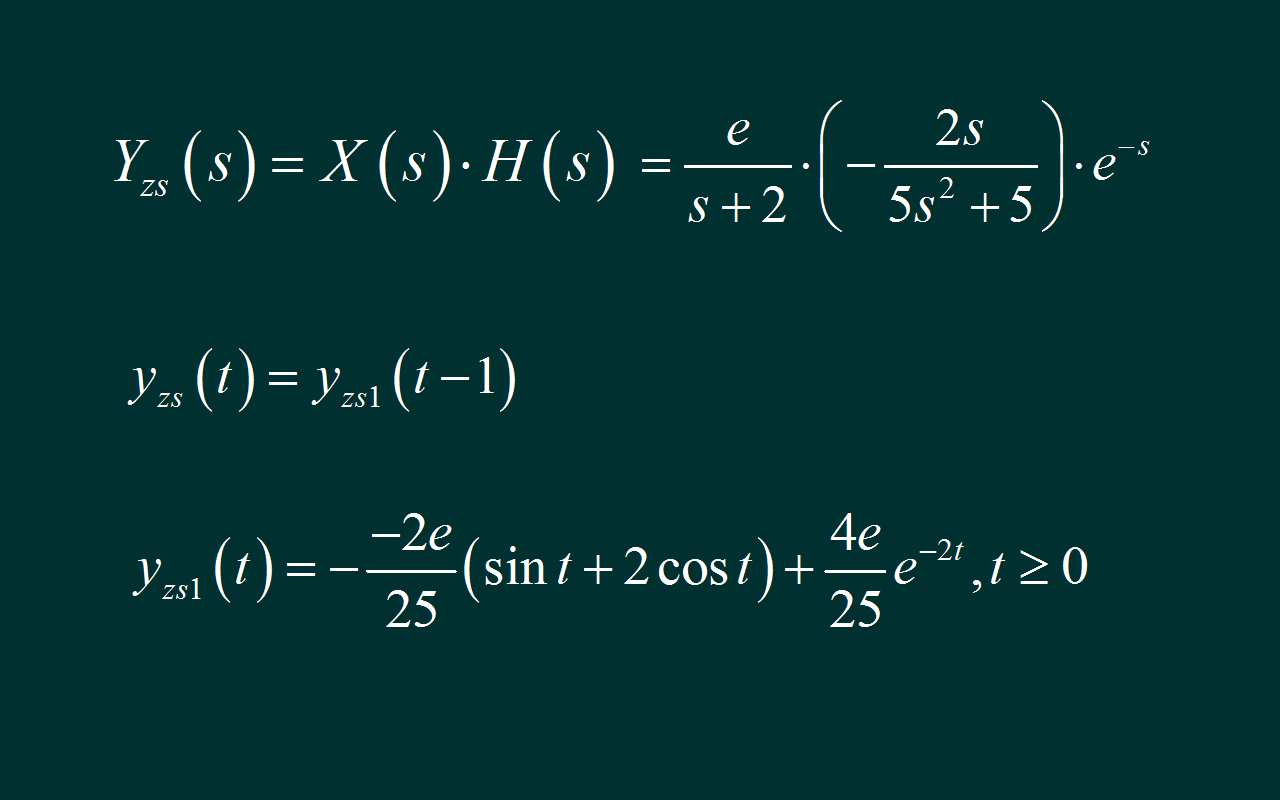
关于系统的稳定系, 可以根据系统极点的分布进行判断。 系统具有一段虚轴 上的共轭极点。 所以系统为不稳定系统。 有的领域也将该系统称为临界稳定系统。
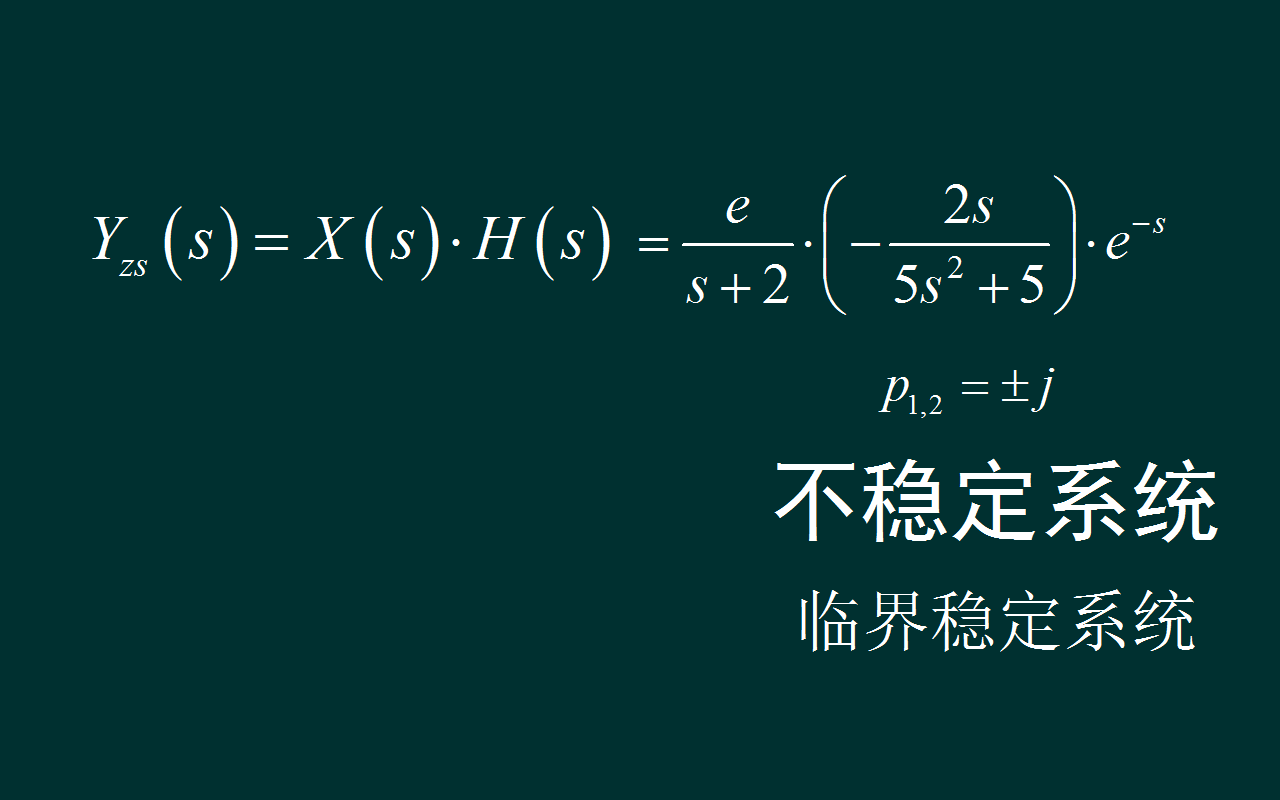
※ 总 结 ※
本文讨论了两个作业习题, 利用系统框图获得系统的系统函数, 并求取系统的零状态响应。
![]()
■ 相关文献链接:
- 信号与系统 2023年春季作业要求与参考答案汇总
- 信号与系统 2023(春季) 作业要求 - 第十二次作业
- 404
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!