Python验证采样定理

Python验证采样定理

• 验证采样定理
• • 采样定理
  • 主要流程
  • 代码
  • • 主函数
    • Change_fs()
    • Change_f0()
    • 完整代码

验证采样定理

采样定理

自行百度

主要流程

在同一图上画出原波形, 抽样点和抽样还原后波形, 并将不同原频率和采样频率动态更新.

代码

主函数

先设置基本参数
f0 #原函数频率
fs #抽样频率
t #横坐标时间
Change_fs() #fs变化时还原函数的变化
Change_f0() #f0变化时还原函数的变化

def main():#输入基本参数f0_List = np.arange(100, 1001, 50)#print(f0)fs_List = np.arange(1000, 99, -50)#print(fs)t = np.arange(0, 0.0101, 0.00001)#print(t)while 1:a = input("键入 1 观察固定频率不同采样率时还原曲线\n\
键入 2 观察固定采样率不同频率时还原曲线\n键入 quit 退出\n")if a == "1":Change_fs(f0_List[2], fs_List, t)elif a == "2":Change_f0(f0_List, fs_List[0], t)elif a == "quit":breakelse:print("无法识别输入QAQ")

Change_fs()

先打开交互模式, 否则不能画动态图.
还原函数时, 利用公式

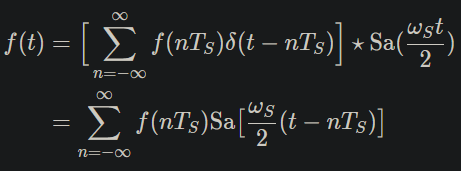
def Change_fs(f0, fs_List, t):F = np.cos(2*np.pi*f0*t)#原函数plt.ion()#开启交互模式plt.figure(figsize=(14, 6))for fs in fs_List:#设置画布外观plt.cla()plt.grid(True)plt.xlim(0, 0.01)plt.ylim(-1, 1)plt.ylabel("Amplitude")plt.title("fo = %ffs"%(f0/fs))##设置横坐标间距x_major_locator=MultipleLocator(0.001)ax=plt.gca()ax.xaxis.set_major_locator(x_major_locator)#设置图像线条Ts = 1 / fsPoints_x = np.arange(-1, 1.001, Ts)Points_y = np.cos(2*np.pi*f0*Points_x)#抽样点fa = []for tt in t:fa.append(np.dot(Points_y, np.sinc(fs*(tt-Points_x))))#抽样后还原函数#画图plt.plot(t, F, "r", label="Orignal Wave")plt.plot(Points_x, Points_y, "*g", label="Sampling Points")plt.plot(t, fa, "-.b", label="Restoration Wave")##设置图例plt.legend(["Orignal Wave", "Sampling Points", "Restoration Wave"],\mode="expand", bbox_to_anchor=(0., 1.07, 1., .07), ncol=3, fancybox=True)plt.pause(0.4)plt.ioff()plt.show()

Change_f0()

原理和Change_fs()一样

def Change_f0(f0_List, fs, t):Ts = 1 / fsPoints_x = np.arange(-1, 1.001, Ts)#抽样点横坐标xplt.ion()#开启交互模式plt.figure(figsize=(14, 6))for f0 in f0_List:#设置画布外观plt.cla()plt.grid(True)plt.xlim(0, 0.01)plt.ylim(-1, 1)plt.ylabel("Amplitude")plt.title("fo = %ffs"%(f0/fs))##设置横坐标间距x_major_locator=MultipleLocator(0.001)ax=plt.gca()ax.xaxis.set_major_locator(x_major_locator)#设置图像线条F = np.cos(2*np.pi*f0*t)#原函数Points_y = np.cos(2*np.pi*f0*Points_x)#抽样点纵坐标yfa = []for tt in t:fa.append(np.dot(Points_y, np.sinc(fs*(tt-Points_x))))#抽样后还原函数#画图plt.plot(t, F, "r", label="Orignal Wave")plt.plot(Points_x, Points_y, "*g", label="Sampling Points")plt.plot(t, fa, "-.b", label="Restoration Wave")##设置图例plt.legend(["Orignal Wave", "Sampling Points", "Restoration Wave"],\mode="expand", bbox_to_anchor=(0., 1.07, 1., .07), ncol=3, fancybox=True)plt.pause(0.4)plt.ioff()plt.show()

完整代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocatordef main():f0_List = np.arange(100, 1001, 50)#print(f0)fs_List = np.arange(1000, 99, -50)#print(fs)t = np.arange(0, 0.0101, 0.00001)#print(t)while 1:a = input("键入 1 观察固定频率不同采样率时还原曲线\n\
键入 2 观察固定采样率不同频率时还原曲线\n键入 quit 退出\n")if a == "1":Change_fs(f0_List[2], fs_List, t)elif a == "2":Change_f0(f0_List, fs_List[0], t)elif a == "quit":breakelse:print("无法识别输入QAQ")def Change_f0(f0_List, fs, t):Ts = 1 / fsPoints_x = np.arange(-1, 1.001, Ts)#抽样点横坐标xplt.ion()#开启交互模式plt.figure(figsize=(14, 6))for f0 in f0_List:#设置画布外观plt.cla()plt.grid(True)plt.xlim(0, 0.01)plt.ylim(-1, 1)plt.ylabel("Amplitude")plt.title("fo = %ffs"%(f0/fs))##设置横坐标间距x_major_locator=MultipleLocator(0.001)ax=plt.gca()ax.xaxis.set_major_locator(x_major_locator)#设置图像线条F = np.cos(2*np.pi*f0*t)#原函数Points_y = np.cos(2*np.pi*f0*Points_x)#抽样点纵坐标yfa = []for tt in t:fa.append(np.dot(Points_y, np.sinc(fs*(tt-Points_x))))#抽样后还原函数#画图plt.plot(t, F, "r", label="Orignal Wave")plt.plot(Points_x, Points_y, "*g", label="Sampling Points")plt.plot(t, fa, "-.b", label="Restoration Wave")##设置图例plt.legend(["Orignal Wave", "Sampling Points", "Restoration Wave"],\mode="expand", bbox_to_anchor=(0., 1.07, 1., .07), ncol=3, fancybox=True)plt.pause(0.4)plt.ioff()plt.show()def Change_fs(f0, fs_List, t):F = np.cos(2*np.pi*f0*t)#原函数plt.ion()#开启交互模式plt.figure(figsize=(14, 6))for fs in fs_List:#设置画布外观plt.cla()plt.grid(True)plt.xlim(0, 0.01)plt.ylim(-1, 1)plt.ylabel("Amplitude")plt.title("fo = %ffs"%(f0/fs))##设置横坐标间距x_major_locator=MultipleLocator(0.001)ax=plt.gca()ax.xaxis.set_major_locator(x_major_locator)#设置图像线条Ts = 1 / fsPoints_x = np.arange(-1, 1.001, Ts)Points_y = np.cos(2*np.pi*f0*Points_x)#抽样点fa = []for tt in t:fa.append(np.dot(Points_y, np.sinc(fs*(tt-Points_x))))#抽样后还原函数#画图plt.plot(t, F, "r", label="Orignal Wave")plt.plot(Points_x, Points_y, "*g", label="Sampling Points")plt.plot(t, fa, "-.b", label="Restoration Wave")##设置图例plt.legend(["Orignal Wave", "Sampling Points", "Restoration Wave"],\mode="expand", bbox_to_anchor=(0., 1.07, 1., .07), ncol=3, fancybox=True)plt.pause(0.4)plt.ioff()plt.show()if __name__ == "__main__":main()

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！