融合耦合因子-直接判决法

融合耦合因子(Convex Combination,CC)算法为了将DD算法中的取最大值和最小值的优点综合起来，平滑因子取值分别为a和b，其中a>b，则两次DD算法的先验信噪比ξm,ka和ξm,kb

因此，ξm,ka的取值接近于DD算法中对前一帧的先验SNR的估计值，在无语音区其取值波动较小，降噪中的音乐噪声产生较少，当语音突然出现时，其估计值明显跟不上瞬时信噪比，这就出现了延时的问题；ξm,kb的取值接近于最大似然的方法估计的当前帧的先验信噪比估计，在无语音区取值波动较大，降噪中音乐噪声残留多，但是在语音突然出现时可以较快的跟踪信噪比的变化，因而估计准确。

CC算法就是加入了耦合因子进行折中，以达到在无语音段耦合因子为0，即得到大的平滑因子的值，在语音突变段耦合因子为1，即可得到较小的平滑因子。

其中，u为耦合因子，范围[0,1]，同DD算法中的平滑因子相似，决定这CC算法的最终估计结果更趋向于ξm,ka还是ξm,kb，为了求出真实的u值，在MMSE准则下构建出最终估计结果和预测估计结果之间的代价函数为

转化得

代价函数对耦合因子求导，令∂J∂μ=0得

其中先验信噪比的真实值ξm,k是未知的，在实际工程中采用最大似然估计ML得到当前帧的先验信噪比估计max(γm,k-1,0)代替真实的先验SNR值ξm,k，则可得如下公式

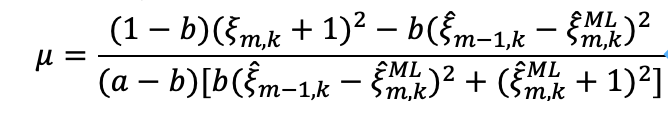
其中a=0.992,b=0.6。

缺点：存在一个问题，当平滑参数取较小值时，估计结果接近于ML方法估计得到先验信噪比估计ξm,kML=max(γm,k-1,0)，即后验信噪比γm,k，此时系统对带噪语音更加敏感，容易产生音乐噪声。

更多文章，关注公众号《音频核》

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！