【数论算法模板】约数、质数、公倍数

约数🍉

若整数n除以整数d的余数为0，即d能整除n,则称d是n的约数，n是d的倍数，记为d|n，言而总之：一个数如果能够被另一个数整除，那么这个数就是另一个数的约数。例如，6是12的约数，因为12可以被6整除。

算术基本定理推论🎈

若正整数N被唯一分解为：

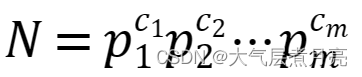
其中ci都是正整数，pi都是质数，且满足p1；即分解质因数操作。

正约数合集🍉

则N的正约数合集可以写作：

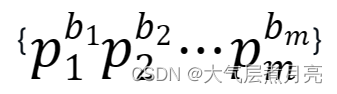
,其中0≤bi≤ci

代码👑

题目：给定n个正整数ai，对于每一个整数ai，请你按照从小到大的顺序输出它的所有约数。

'''
# #AC Code（正约数合集)# #
'''
# 导入包用于求平方根math.sqrt
import math
# 分解质因数将N分解为p1^c1*p2^c2...*pm^cm的形式（核心）                         
def solve(n):#用于存放正约数合集res = [] # 遍历[1,sqrt(n)]，时间减少sqrt(n)for base in range(1, int(math.sqrt(n) + 1)):# 如果base可以被n整除if n % base == 0 :# 把base是n的正约数，放入正约数合集res.append(base)# 时间减少到sqrt(n),如果n除以base不等于base,即16//2=8,那么8也是16的正约数；# 防止重复放，如：4*4=16, 有两个4；（完全平方数情况不再次放）if n // base != base:res.append(n//base)# 从小到大for v in sorted(res):# 打印结果print(v,end=' ')print()
# 主函数
if __name__ == '__main__':for _ in range(int(input())):solve(int(input()))

思路：求一个数的正约数只需要从1遍历到它的平方根，假设一个数为n=16，那么它的正约数合集为[1, 2, 4, 8, 16]，那为什么我们不需要遍历[1,16]呢，因为我们只需要求出[1, 2, 4]，便可以得到[8, 16]，

·只需要使得16除以1便可以得到16，

·只需要使得16除以2便可以得到8，

·只需要使得16除以4便可以得到4，但是被除数4等于除数4，所以选择不放入。

偶数比较好理解，接下来我们看看奇数，假设一个数n=15,那么它的正约数合集为[1, 3, 5, 15]，同样的只需要遍历[1, int(sqrt(15))]=[1,3]，那么：

·只需要使得15除以1便可以得到15，

·只需要使得15除以3便可以得到5。

正约数个数（多个数乘积的约数个数）🍉

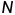的正约数个数为：

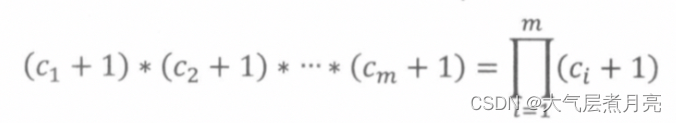
代码👑

题目：给定n个正整数ai，请你输出这些数的乘积的约数个数，答案对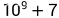取模。

'''
# #AC Code（多数之乘值的正约数个数)# #
'''
#分解质因数
primes = {}
t = int(input())
for _ in range(t):n = int(input())base = 2while base*base <= n:while n%base == 0:if base not in primes:primes[base] = 1else:primes[base] += 1n //= basebase += 1if n > 1:if n not in primes:primes[n] = 1else:primes[n] += 1res = 1
mod = 1e9+7
for each in primes:res *= primes[each] + 1 % mod
print(int(res% mod))

思路：该题为求多个数相乘之后的正约数的个数，根据公式，我们只需要求出每个数的质因数，那么接着按照公式相乘便可。

正约数之和（多个数乘积的约数之和）🍉

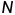的正约数之和为：

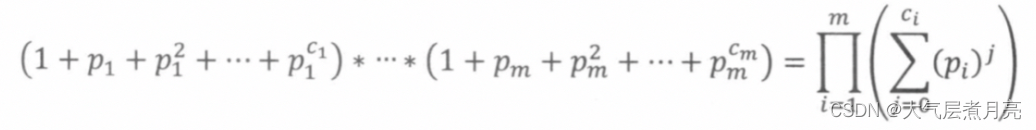
代码👑

题目：给定n个正整数ai，请你输出这些数的乘积的约数之和，答案对10**9+7取模。

'''
# #AC Code（多数之乘值的正约数之和)# #
'''
primes = {}
t = int(input())
for _ in range(t):n = int(input())base = 2while base * base <= n:while n % base == 0:if base not in primes:primes[base] = 1else:primes[base] += 1n //= basebase += 1if n > 1:if n not in primes:primes[n] = 1else:primes[n] += 1def quick_pow(a, n):res = 1while n:if n&1:res *= a % modn >>= 1a *= a % modreturn int(res%mod)res = 1
mod = int(1e9 + 7)
for each in primes:cnt = 0for pow in range(primes[each]+1):cnt += quick_pow(each, pow)res *= cnt
print(int(res%mod))

思路：该题为求多个数相乘之后的正约数之和，根据公式，我们只需要求出每个数的质因数，那么接着按照公式计算便可。

求最大公约数🍉

题目：给定n对正整数(ai,bi),请你求出每对数的最大公约数。

AC Code👑

'''
# #AC Code（最大公约数)# #
NOTE： 加载输入“n对正整数”。
'''
def load_dataest():n = int(input())dataset = []for _ in range(n):dataset.append(list(map(int, input().split())))return n, dataset
def gcd(a, b):return a if b==0 else gcd(b,a%b)
def lcm(a, b):return a * b // gcd(a, b)if __name__ == "__main__":n, dataset = load_dataest()for i in range(n):a, b = dataset[i]print(gcd(a, b))

思路：求两个正整数 a 和 b 的 最大公约数 d，则有 gcd(a,b) = gcd(b,a%b)

证明：

设a%b = a - k*b 其中k = a/b(向下取整)，

若d是(a,b)的公约数 则知 d|a 且 d|b 则易知 d|a-k*b 故d也是(b,a%b) 的公约数，

若d是(b,a%b)的公约数 则知 d|b 且 d|a-k*b 则 d|a-k*b+k*b = d|a 故而d同时整除a和b 所以d也是(a,b)的公约数，

因此(a,b)的公约数集合和(b,a%b)的公约数集合相同 所以他们的最大公约数也相同，

证毕。

线性筛筛素数——时间复杂度：O(n)🍉

给定一个正整数n,请你求出1~n中质数的个数。

输入格式

共一行，包含整数n。

输出格式

共一行，包含一个整数，表示1~n中质数的个数。

数据范围

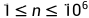
输入样例：

8

输出样例：

4

AC Code👑

'''
# #AC Code（线性筛筛质数)# #
'''
def load_dataset():return int(input())def linear_siere(n):st = [False for _ in range(n+1)] primes = []for i in range(2, n + 1):if not st[i]: primes.append(i)for p in primes:    # 遍历素数列表if p * i > n: break  # 如果 p*i 已经大于 n 了没必要再筛了  st[p*i] = True      # 满足条件筛掉 p/iif i % p == 0: break # i是p的倍数(即p是i的最小质因子)，就不用再继续了#  换句话说，之前已经筛过一次了# 但是还是需要用最小质因子来筛的所以放在筛的式子的下面print(len(primes))if __name__ == "__main__":linear_siere(load_dataset())

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！