数字信号处理（4）- 离散时间信号傅里叶变换（DTFT)

目录

1 DTFT的基本概念

2 DTFT正反变换的由来

3 DTFT的共轭对称性质

3.1 共轭的概念 

3.2 序列的表示方法

3.3 DTFT对称性的性质 

1 DTFT的基本概念

一个离散信号及其频谱的关系，可以用离散时间信号（序列）的傅里叶变换表示。

 说明：

常用序列的傅里叶变换： 

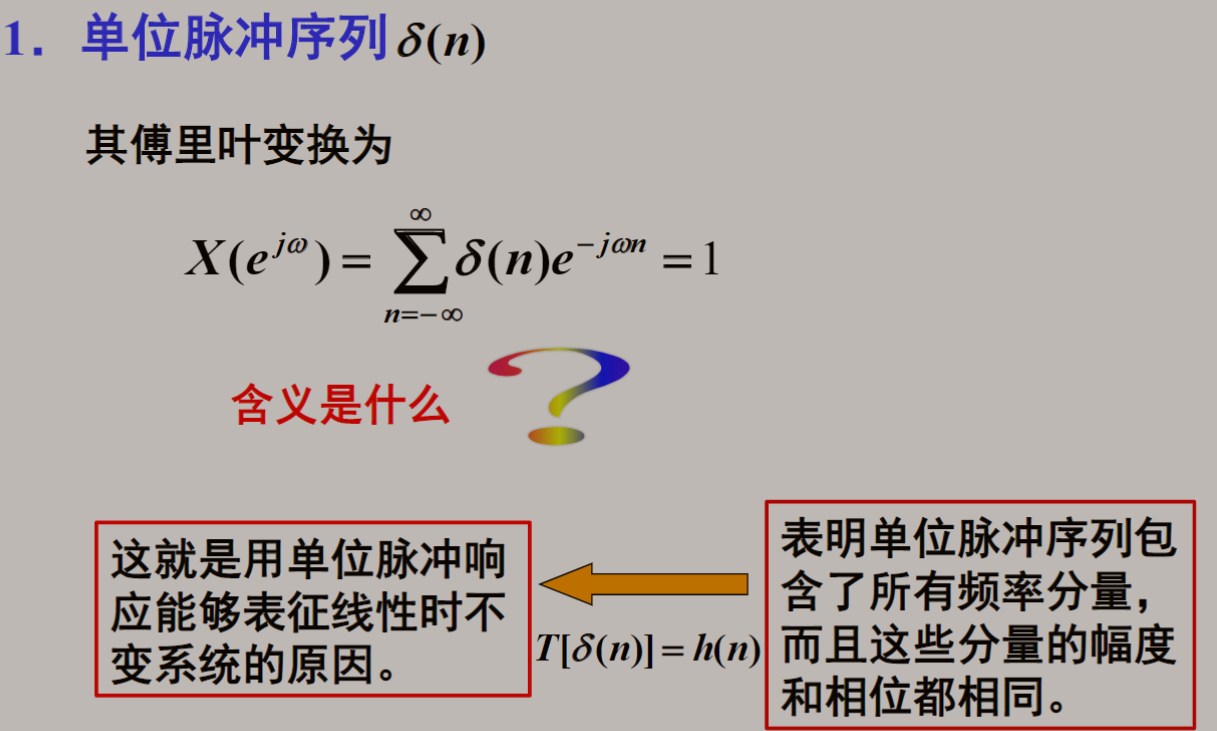
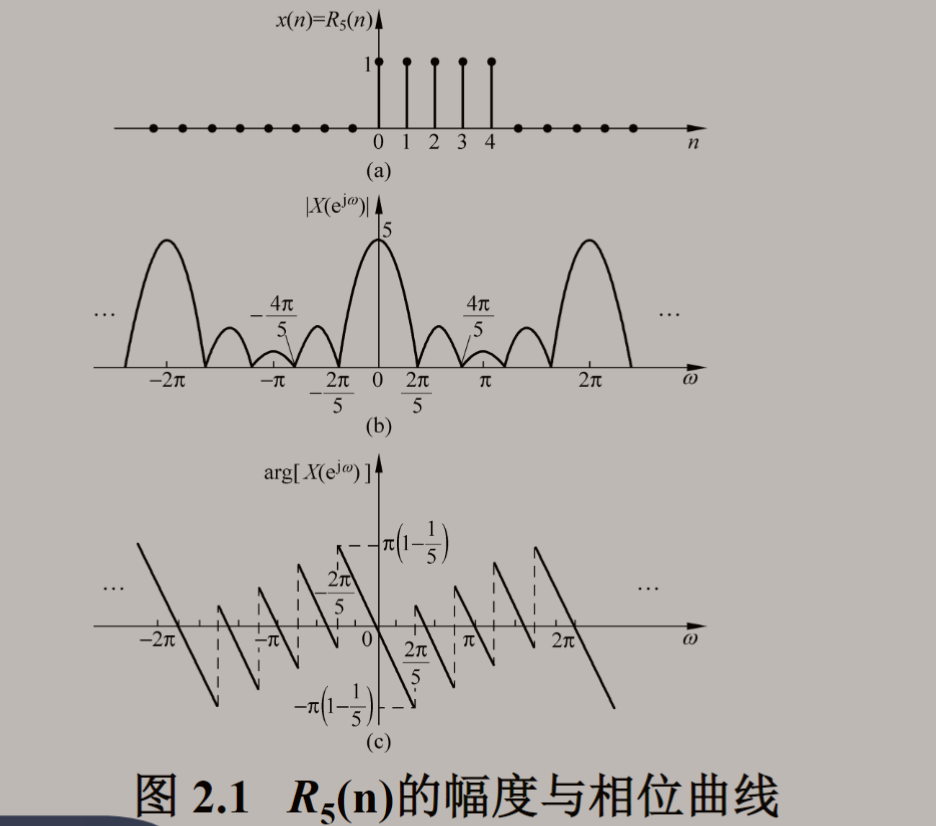
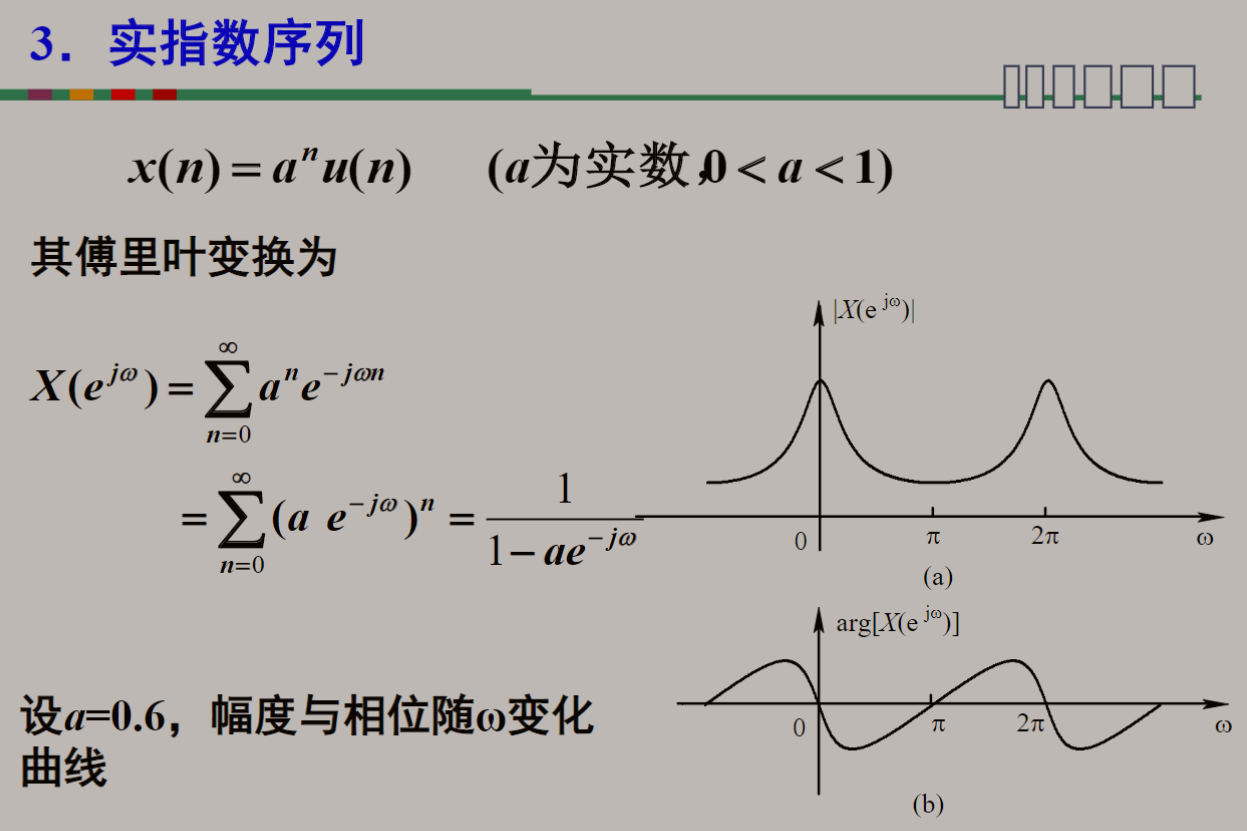
2 DTFT正反变换的由来

3 DTFT的共轭对称性质

3.1 共轭的概念 

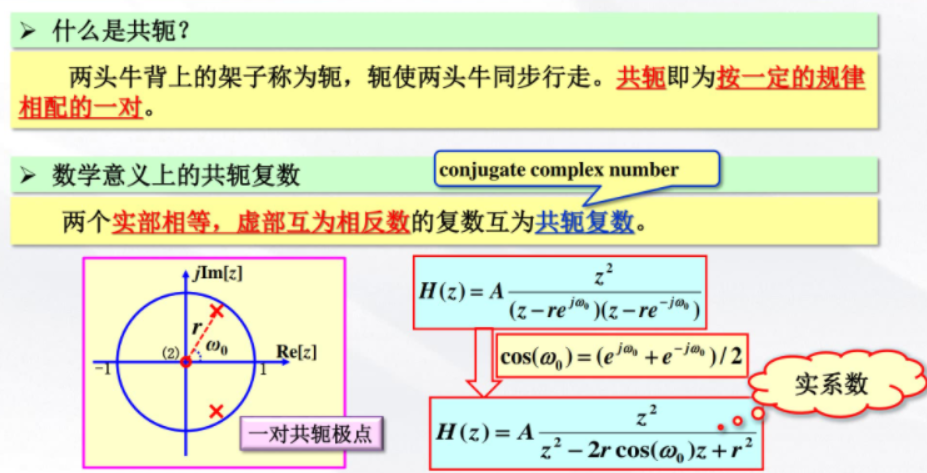
 极点共轭对称，差分方程的系数全是实系数，有利于工程上实现差分方程。

3.2 序列的表示方法

任何序列均可表示为实部和虚部之和

这里再引入和

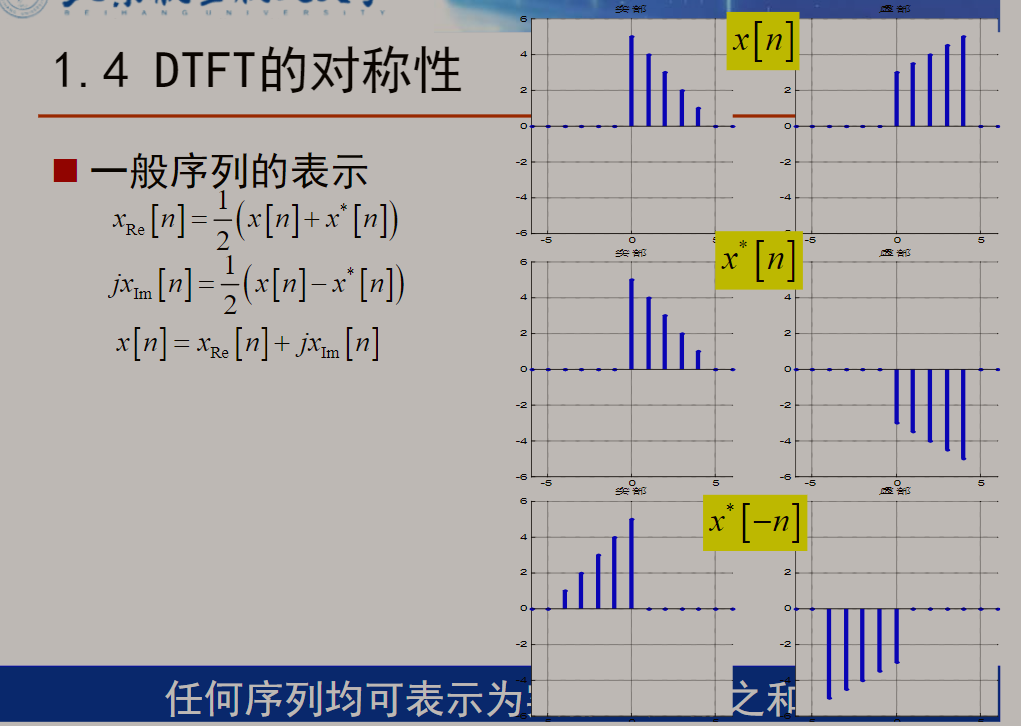
 与实部偶对称，虚部奇对称。

推出，发现其具有共轭对称性，其自身实部偶对称，虚部奇对称

 推出，发现其具有共轭反对称性，其自身实部奇对称，虚部偶对称

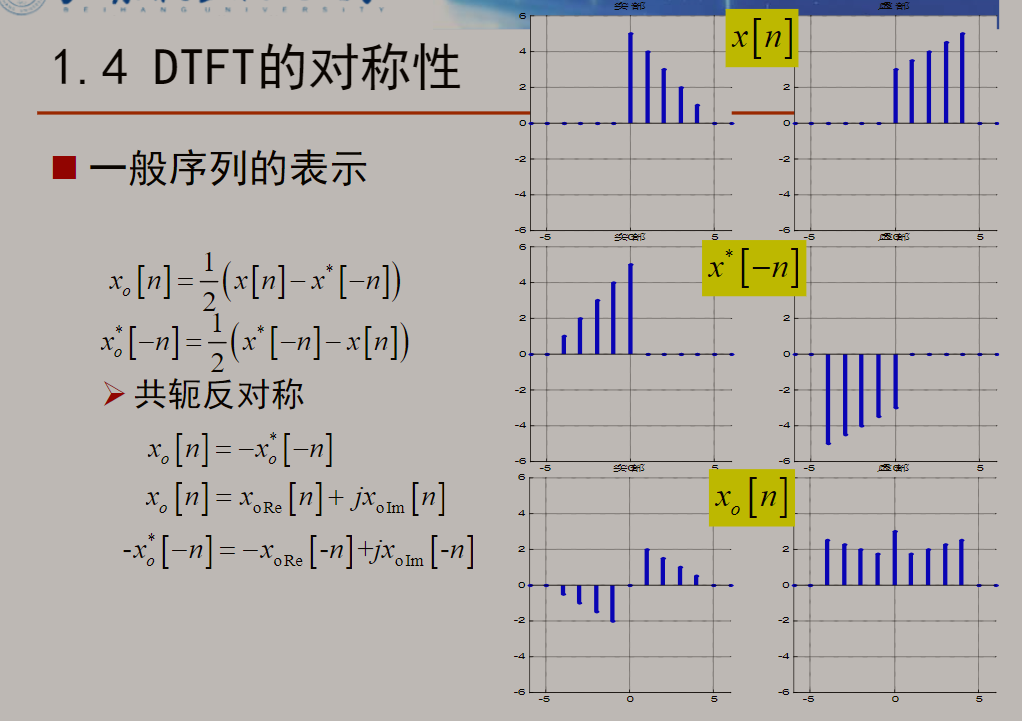
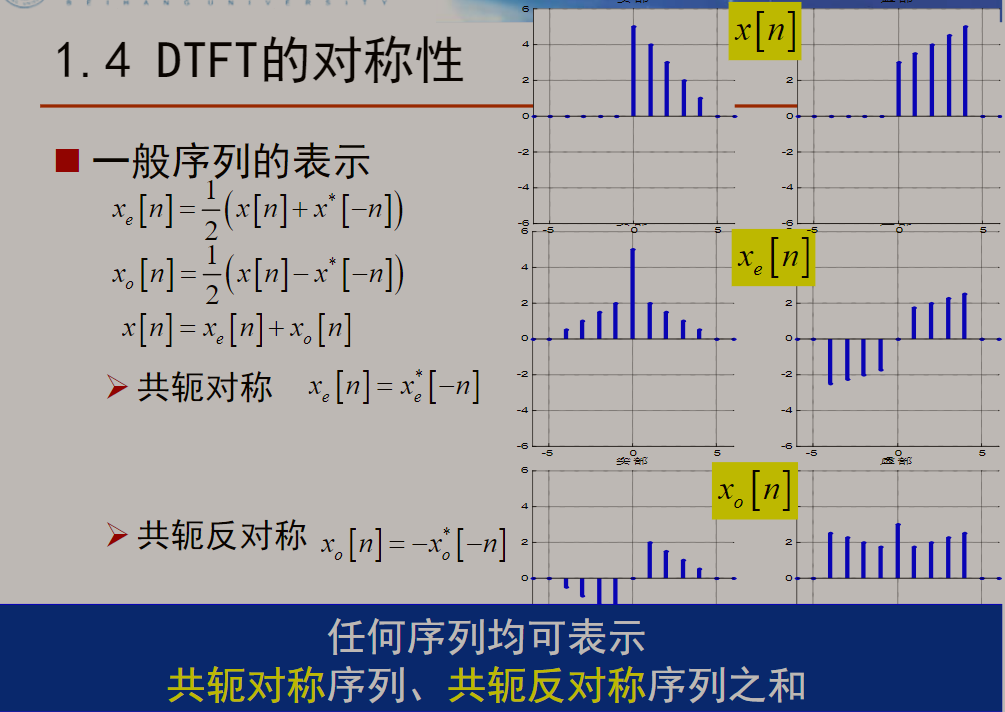
因此可用共轭对称序列和共轭反对称序列之和表示一般序列。

总结： 

3.3 DTFT对称性的性质 

注：这是两个频率响应之间的关系。

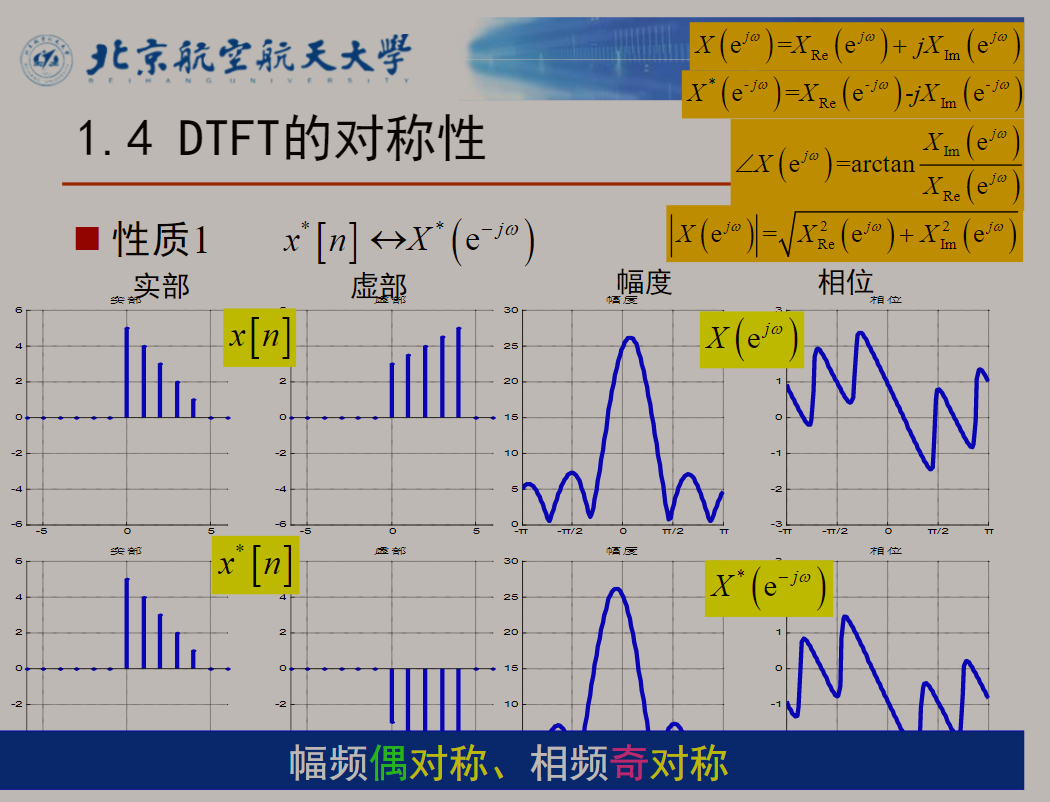
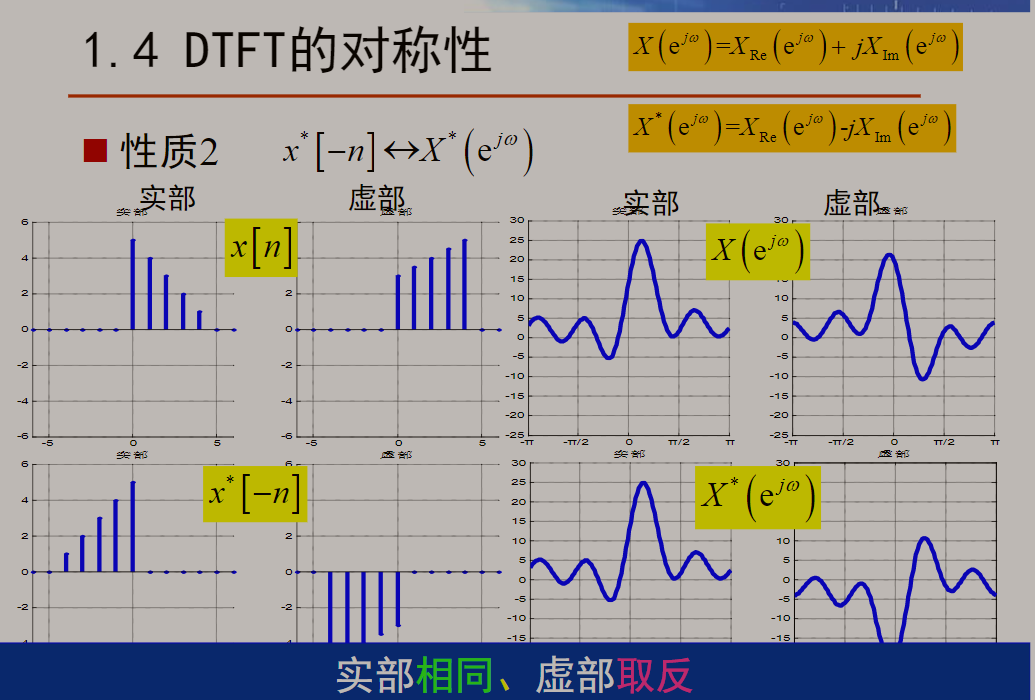
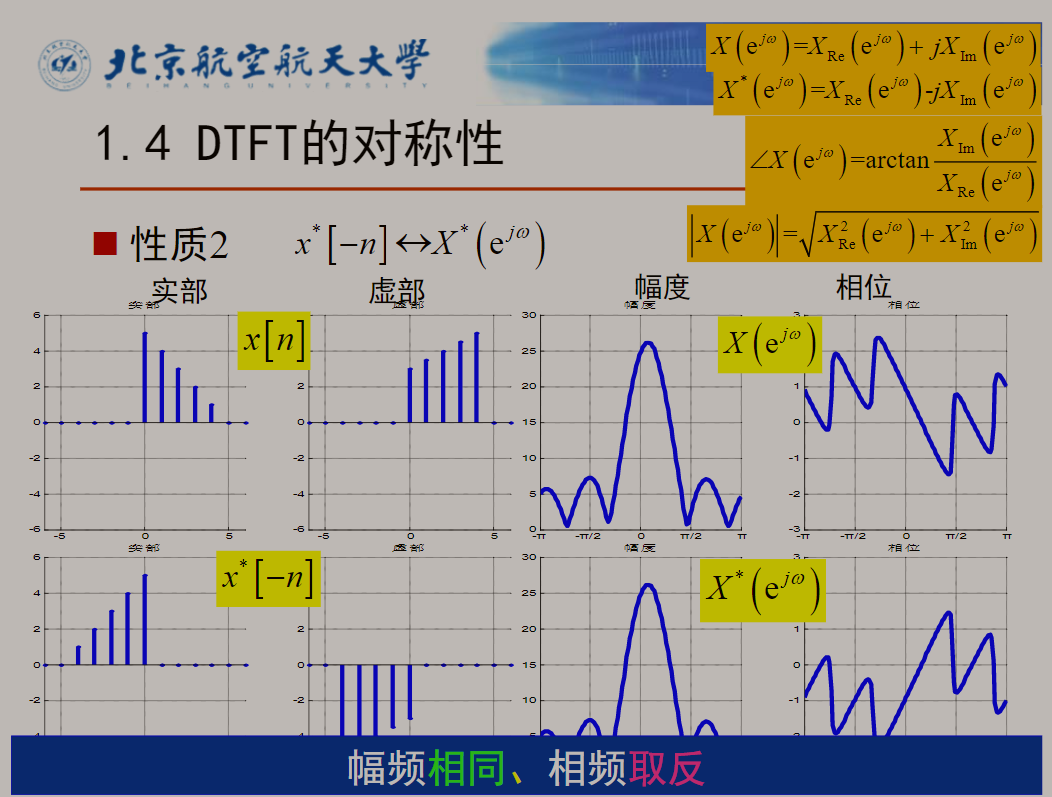
由这三个公式可加以推广对称性质： 

 总结：

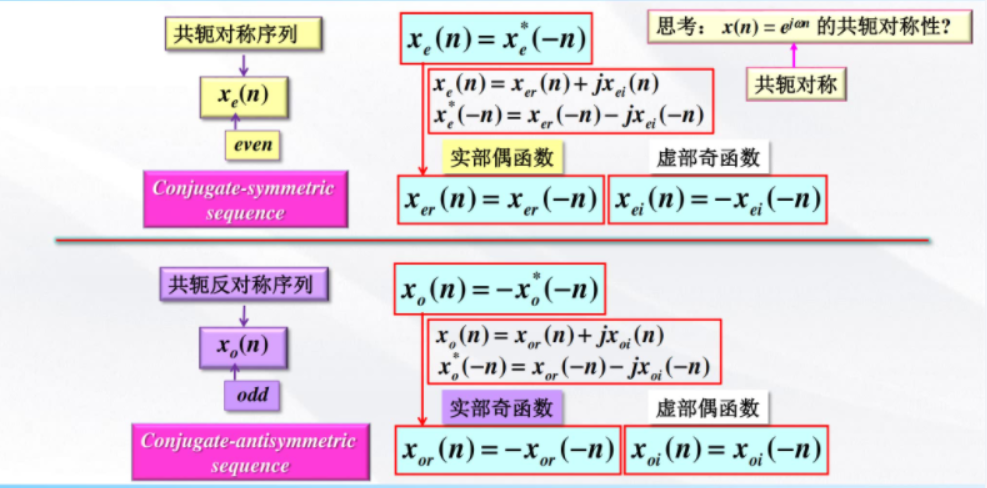
频域函数的共轭对称性质描述： 

时域与频域对应的共轭对称性质： 

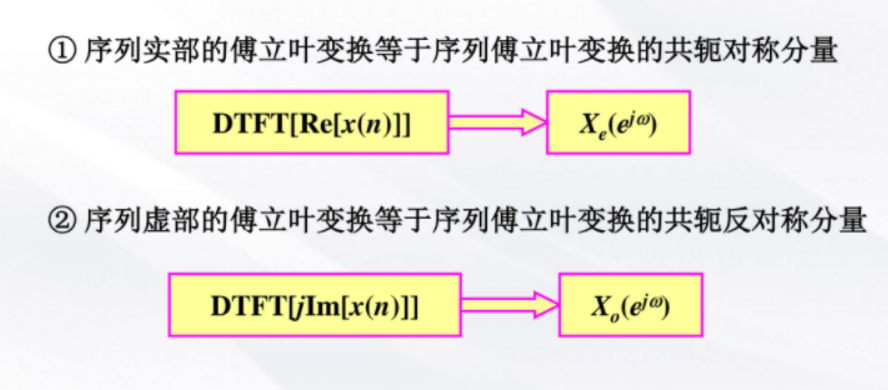
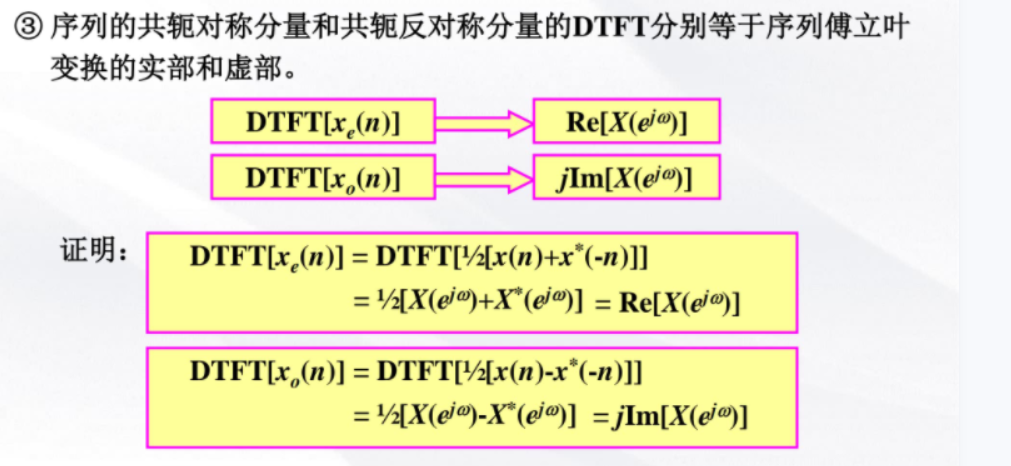
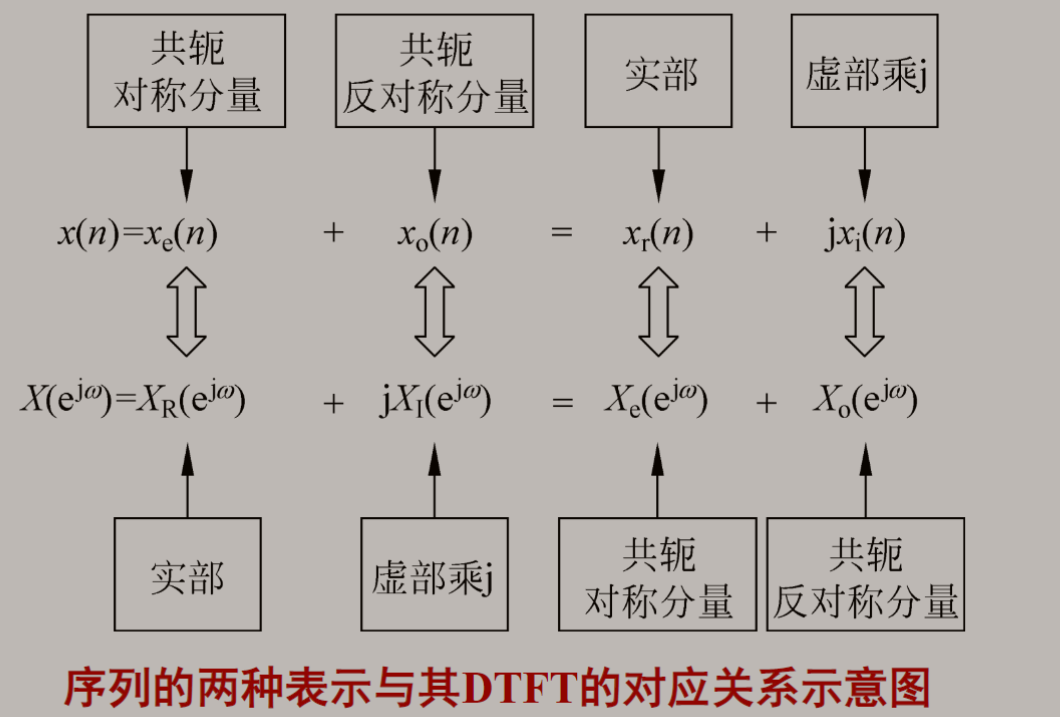
 若x(n)为实序列：

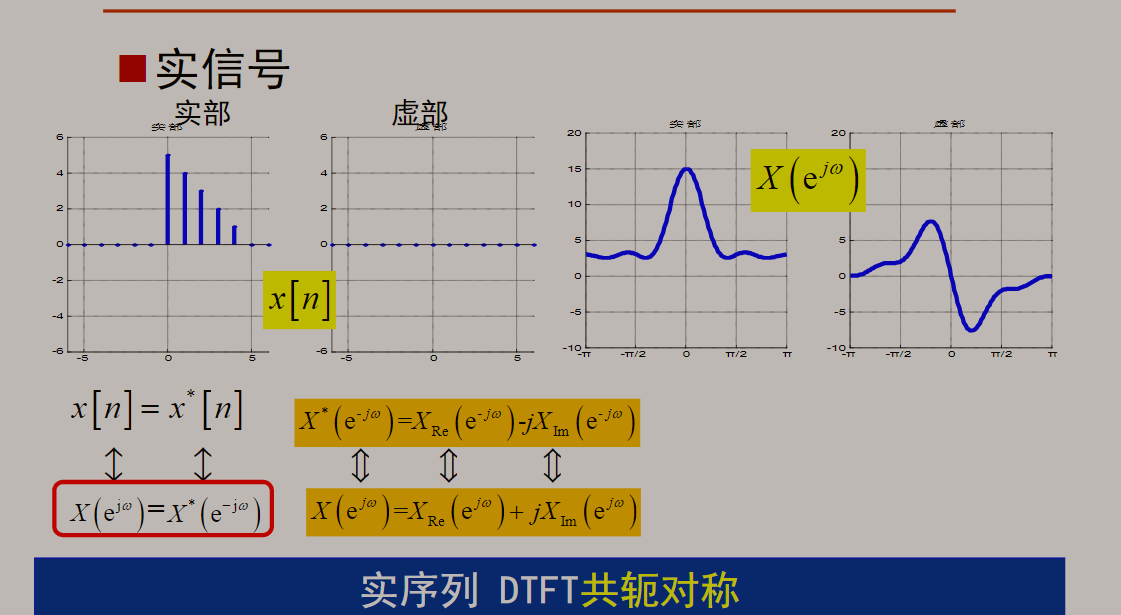
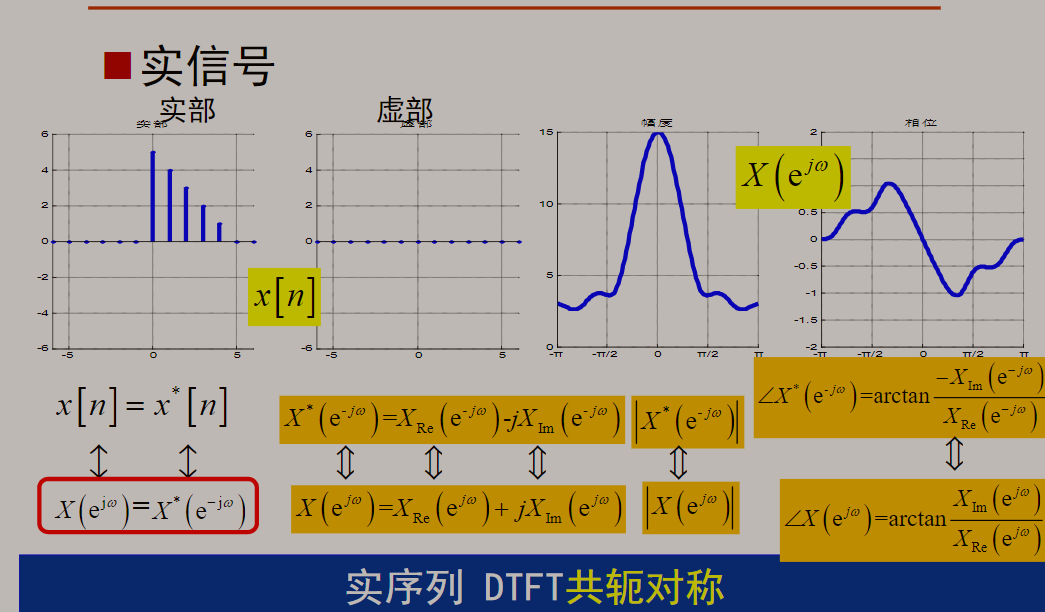
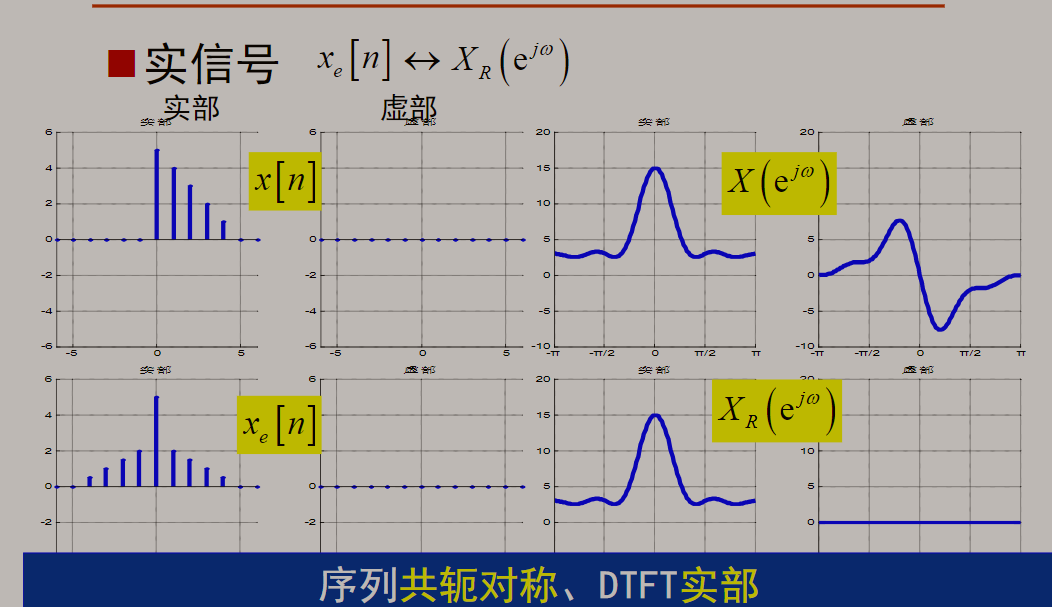
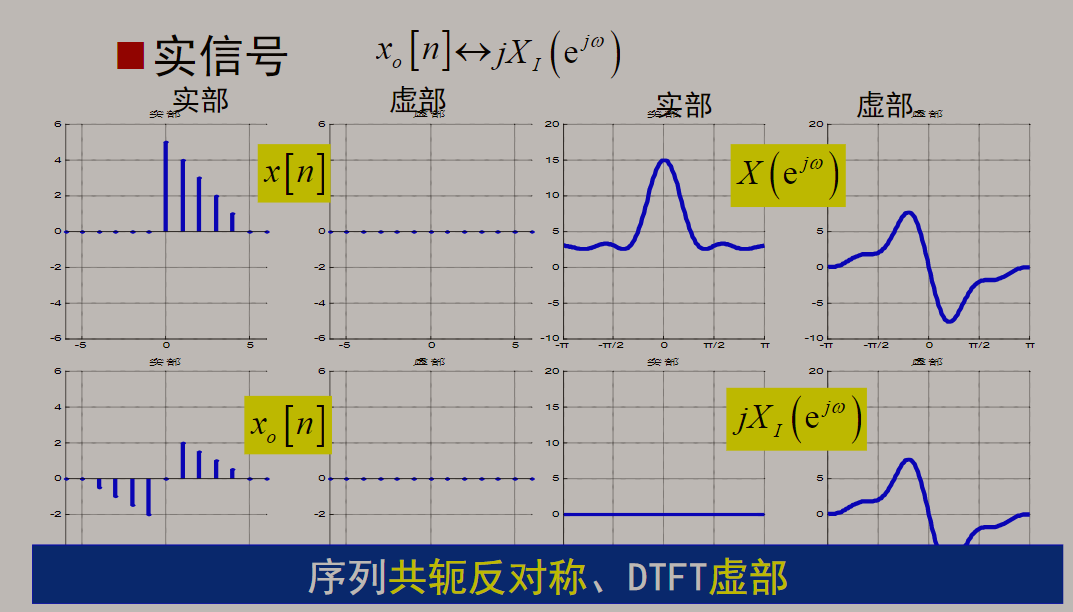
总结： 

 此外DTFT的性质还有：线性、时移、频移、时域卷积定理、频域卷积定理（复卷积定理）、周期性、帕斯瓦尔定理（Parseval)......这里不再赘述。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！