文章目录

• 一、实验目的
• 二、实验平台
• 三、实验内容与结果：
• • 3.1题目分析
  • 3.2实验代码:
  • 3.3结果与分析：
  • 3.4实验总结
  • 知识点总结:

一、实验目的

数据：自选或train.csv

1. 实现移动平均；
   a) 一次移动平均，取多个n值，计算标准差；
   b) 二次移动平均，计算参数a,b，进行预测；

2. 实现指数平滑。
   a) 一次指数平滑，取多个a值；
   b) 二次指数平滑（可选）；

二、实验平台

Python 3.7

三、实验内容与结果：

3.1题目分析

实现移动平均分析:
一次移动平均的公式:

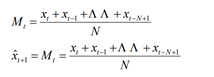
标准差的公式即为MSE公式开根号:

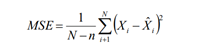
二次移动平均公式:

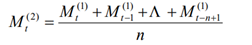
二次移动平均预测法的预测模型(解析过程中默认了t为最后一期数据，T为1):

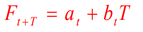
a和b的计算公式:

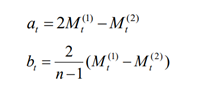
实现指数平滑分析:
一次指数平滑公式:

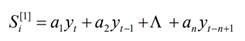
二次指数平滑公式:

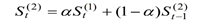
预测模型以及a和b的值:

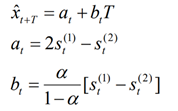
依题意得，就是读入数据，然后带入公式就行

3.2实验代码:

# -*- codeing =utf-8 -*-
# @Time : 2021/4/15 15:13
# @Author : ArLin
# @File : demo2.py
# @Software: PyCharm
import csv
from collections import deque
import numpy
import numpy as np#读取csv文件
def ReadCsvFile(path):File = open(path, 'r')f = csv.reader(File)i = 0data = []for row in f:if i > 0:#去头处理data.append(int(row[2]))i = i + 1return datadef MovingAverage(data,n): #移动平均法ForecastN=len(data)+1d1=deque()P_data=[]for i in data:d1.appendleft(i)if len(d1) == n:P_data.append(np.round(sum(d1) / len(d1),1))d1.pop()return P_data
#计算标准差
def Forecast_Standard_Deviation(data,Pdata,n):s = []sn = 0for index in range(len(Pdata) - 1):s1 = (Pdata[index] - data[n + index]) ** 2 #标准差公式s.append(np.round(s1, 1))y =int((sum(s) / len(s)) ** 0.5)print('N为:',n,'时，一次移动平均计算出的标准差:',y)return y
#计算A和B的值和预测值
def CountAandB(P1data,P2data,n):for index in range(len(P2data)):a1=2*P1data[index+n-1]-P2data[index] #a的公式b1=(2/(n-1))*(P1data[index+n-1]-P2data[index])#b的公式if index==len(P2data)-1:a11=int(a1)b11=int(b1)F = a11 + b11#默认T为1的情况计算Fprint('N的值为:',n,'时，a的值为:',a11,'b的值为:',b11,'二次移动平均预测法的预测值为:',F)return a11,b11#一次，二次指数平滑值
def One_and_TwoOrderExponentialSmoothing(data,a):s1=[]s2=[]s0 = (data[0] + data[1] + data[2]) / 3s1.append(np.round(s0, 2))s2.append(np.round(s0, 2))for index in range(len(data)):si1=a*data[index]+(1-a)*s1[index]s1.append(np.round(si1, 2))si2=a*s1[index+1]+(1-a)*s2[index]s2.append(np.round(si2, 2))print('当a为',np.round(a, 1), '时，一次指数平滑值为:', s1[len(data)])return s1,s2
#预测模型以及a和b的值
def ABExponentialSmoothing(s1,s2,A):for index in range(len(s2)):a1 = 2 * s1[index]-s2[index]b1 = (A/(1-A))*(s1[index]-s2[index])if index == len(s2)-1:a11= np.round(a1, 2)b11= np.round(b1, 2)F = a11+b11print('A的值为:',np.round(A, 1), '时，a的值为:', a11, 'b的值为:', b11, '二次指数平滑值的预测值为:', np.round(F, 2))return a11, b11def allMovingAverage(data,n):P1_data = MovingAverage(data, n)P2_data = MovingAverage(P1_data, n)Forecast_Standard_Deviation(data, P1_data, n)CountAandB(P1_data, P2_data, n)if __name__ =='__main__':path='train.csv'data=ReadCsvFile(path)for i in range(2,18):allMovingAverage(data,i)for i in numpy.arange(0.1, 1, 0.1):s=One_and_TwoOrderExponentialSmoothing(data, i)ABExponentialSmoothing(s[0],s[1],i)

3.3结果与分析：

结果截图:
移动平均结果截图:

指数平滑实验结果截图:

实验结果分析:
从移动平均结果截图中我们可以看出，
在选取从2-20的多个n值中，
当n=2时，一次移动平均计算出的标准差最小，为46。
而从指数平滑实验结果截图中我们可以看出在选取0.1-1的多个a值中
平滑系数a对预测精度影响很大, a越大（接近于1），表示模型越来越重视近期数据的作用，对过程的变化反映越快；
a越小，表示模型越重视离现时更远的历史数据的作用，对过程变化的反映越迟钝。

3.4实验总结

出现的问题与解决方法:

问题1:
读取csv的时候报错
<_csv.reader object at 0x0000026E7F21BCE0>
原代码:

File=open(r'train.csv','r')
f=csv.reader(File)
print(f)

解决方法:
因为csv.reader返回的是一个迭代类型，索引应该用循环来打印信息才行
修改后的代码:

File=open(r'train.csv','r')
f=csv.reader(File)
#print(f)
for row in f:print(row)

问题2:
刚开始在保留小数位的时候我采用的是’%.xf’方法后面发现这个貌似只能在print中使用，达不到我的预期，我就又使用了format函数但是导致保留进列表的数据是字符串的形式，就导致多了一步操作
解决方法:
最后我采用了round()函数，发现是最省时省力的了。

问题3:
其实一开始我写的预测模式的t和T是可以自定义的，但是由于数据量非常大，处理起来就会很麻烦，很繁琐
解决方法:
虽然我实现了这个算法函数，但是经过和同学沟通后还是决定把t定为最后一位数据，T为1

知识点总结:

1. 移动平均:
   以计算算术平均数为基础的算法，适用对象为: 一组随时间变化而波动的数据, 时间序列变动不太剧列，较平稳。方法是每次在时间序列上移动一步求平均值，作用是能消除季节性变动、周期性变动与随机变动的影响， 突出长期趋势
2. 指数平滑:
   初始值的确定:
   时间序列原始值较多， a较大时可取s0(1)=x1,s0(2)=s0(1)
   数据点不多，初始值对预测精度影响较大时，可取开始几个观测值的算术平均值、加权平均值做初始值。
   a的影响:
   平滑系数a对预测精度影响很大, a越大（接近于1），表示模型越来越重视近期数据的作用，对过程的变化反映越快；a越小，表示模型越重视离现时更远的历史数据的作用，对过程变化的反映越迟钝。
   a的取值经验(通常0.01  初始值不可靠时,a倾向取大
    原始数据波动大时, a倾向取大,反之亦反
   3. python保留小数位的三种实现方法
   format函数
   '%.xf’方法
   round()函数

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！