1、奈奎斯特准则

        连续模拟信号以离散的时间间隔t s = 1/fs 采样，该时间间隔必须精心选择，确保采样数据能 精确描述原始模拟信号。很显然，采样越多(采样速率越快)，模拟信号的数字表示就越精 确。如果采样较少(采样速率较慢)，则少到某一点时，模拟信号的关键信息将因得不到采 样而丢失。在贝尔电话实验室工作期间，Harry Nyquist分别于1924和1928年发表了两篇经 典论文，奠定了采样的数学基础。之后不久，R. V. L. Hartley对Nyquist的原始工作进行了补充，这些论文构成了上世纪40年代PCM工作的基础，而后在1948年Claude Shannon撰写了其在通信理论方面的经典论文。

         简而言之，奈奎斯特准则要求采样频率至少是信号所含最高频率的两倍，否则信号所承载的信息将会丢失。如果采样频率小于最大模拟信号频率的两倍，将会出现一种称为“混叠” 的现象。

        下图示例中，采样频率f s 并未达到至少2fa ，而仅仅是略大于模拟输入频率f a ，因而违背 了奈奎斯特准则。注意，实际样本的图案产生了较低频率(fs – fa )的混叠正弦波

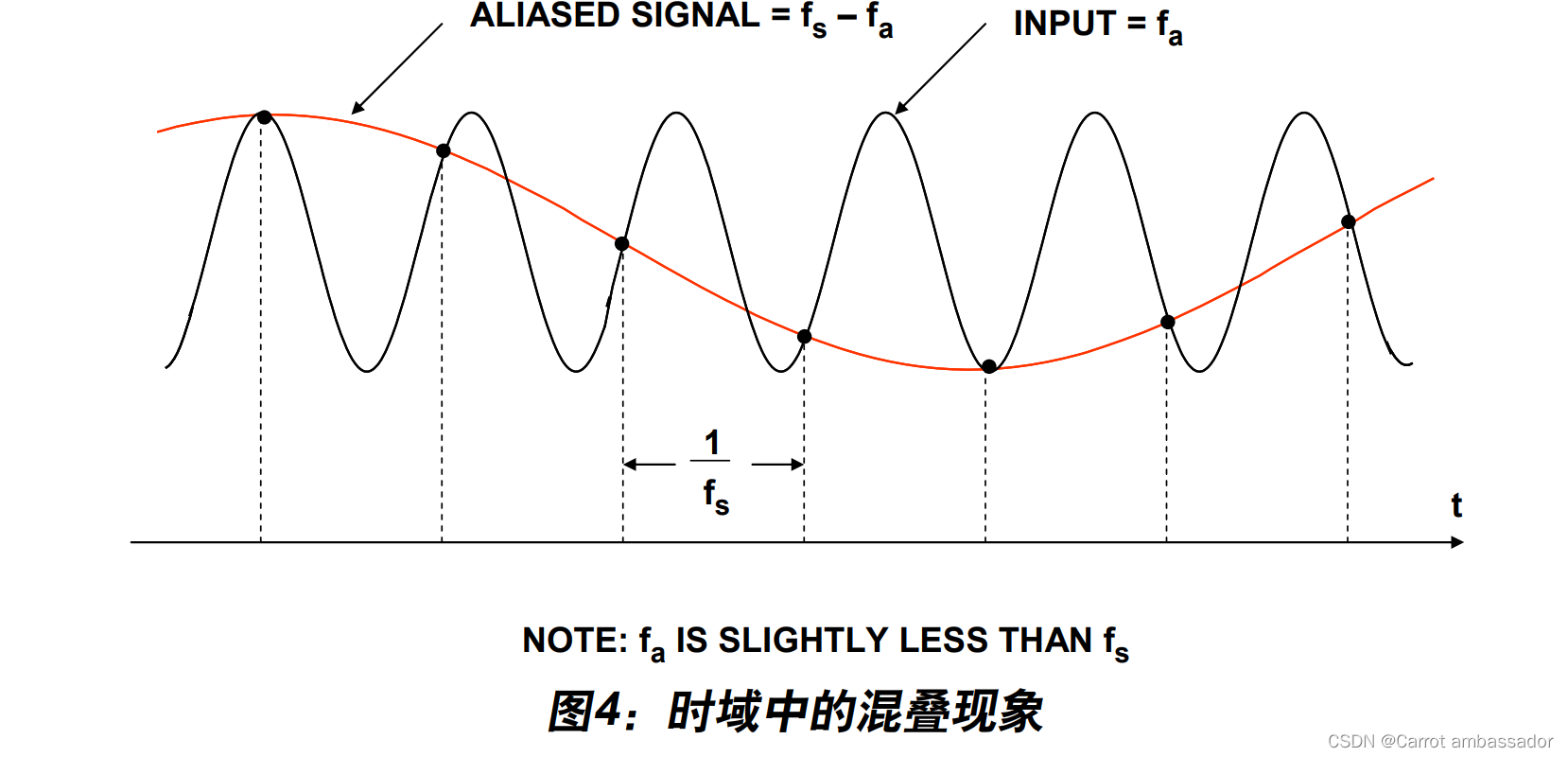
         这种情况的对应频域表示如下图所示。现在考虑采用理想的脉冲采样器以f s 的频率对频率为f a 的单频正弦波进行采样(见图5A)。另外假定f s > 2fa ，如图所示。采样器的频域输出显示每数个f s 附近均会出现原始信号的混叠或镜像，具体位于|± Kfs ± fa |，K = 1, 2, 3, 4, ....

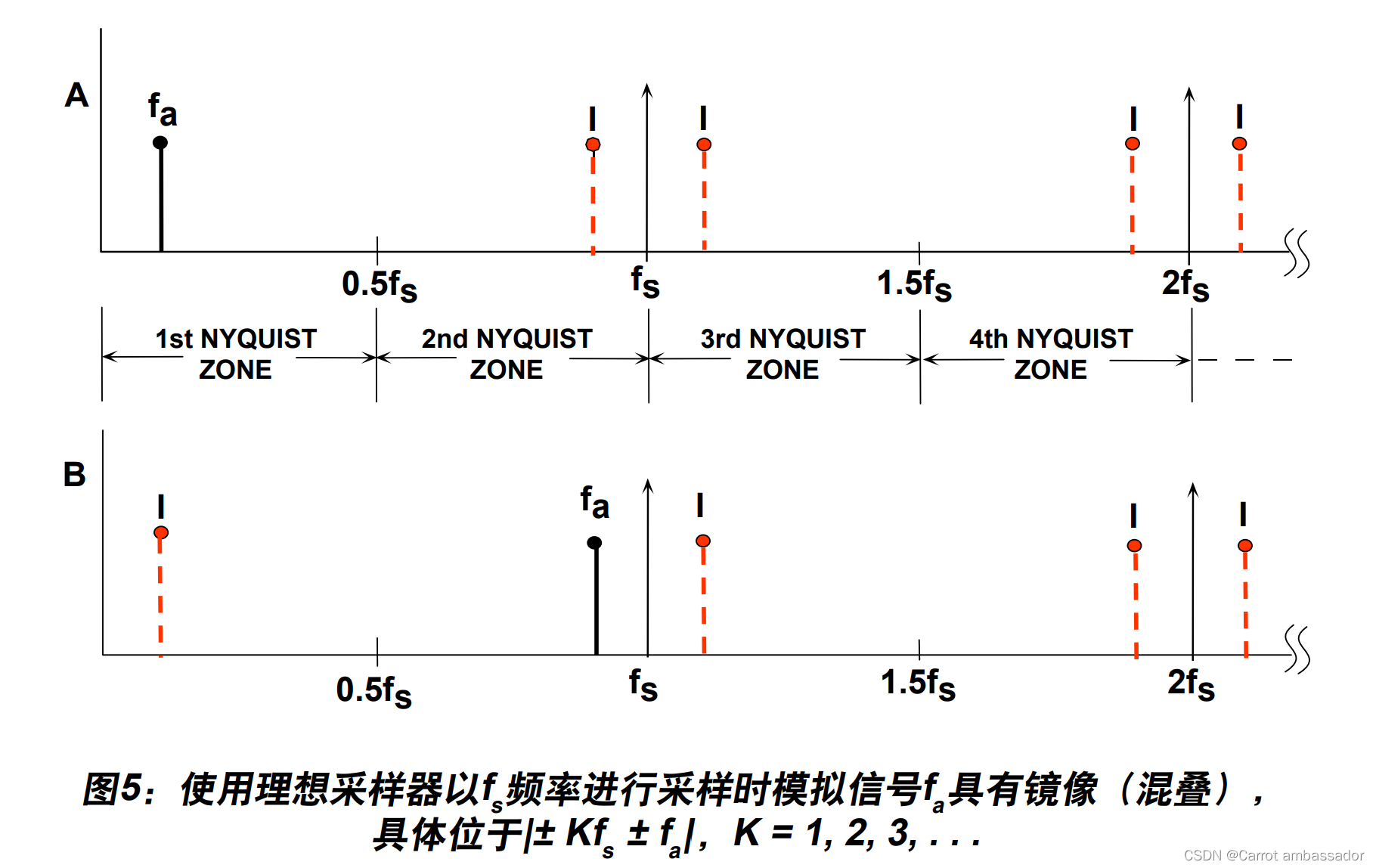
         奈奎斯特带宽定义为从DC到f s /2的频谱。该频谱可细分为无数奈奎斯特区，每个宽度等于 0.5fs ，如图所示。在实际操作中，理想采样器可以替换为后接FFT处理器的ADC。FFT处理器仅提供DC到f s /2范围内的输出，即第一奈奎斯特区出现的信号或混叠。

       接下来，我们考虑第一奈奎斯特区之外的信号情况(图5B)。信号频率仅仅略小于采样频率，对应图4中时域表示所示的条件。注意，即使信号位于第一奈奎斯特区之外，其镜像 (或混叠)f s – fa 仍位于该区内。现在回到图5A。很明显，如果任何镜像频率f a 处出现干扰信 号，那么也将会出现在f a 处，因而会在第一奈奎斯特区内产生杂散频率成分。

        这类似于模拟混频过程，同时意味着需要在采样器(或ADC)之前放置一些滤波器件来消除 位于奈奎斯特带宽之外但其混叠成分又位于该范围之内的频率成分。滤波器性能将取决于带外信号与f s /2的接近程度和所需的衰减量。

2、基带抗混叠滤波器

        基带采样意味着要采样的信号位于第一奈奎斯特区之内。需要注意的是，当理想采样器的输入端没有输入滤波时，任意奈奎斯特区内奈奎斯特带宽之外的任意频率成分(信号或噪 声)都将混叠回到第一奈奎斯特区。为此，几乎所有采样ADC应用中都会使用抗混叠滤波 器来消除这些干扰信号。

        合理指定抗混叠滤波器是非常重要的。第一步是了解待采样信号的特性。假定最高目标频率为f a 。抗混叠滤波器任由DC至f a 范围内的信号通过，同时对f a 以上的信号进行衰减。

        假定所选滤波器的转折频率等于f a 。系统动态范围内从最小衰减到最大衰减的有限跃迁效应如图6A所示。

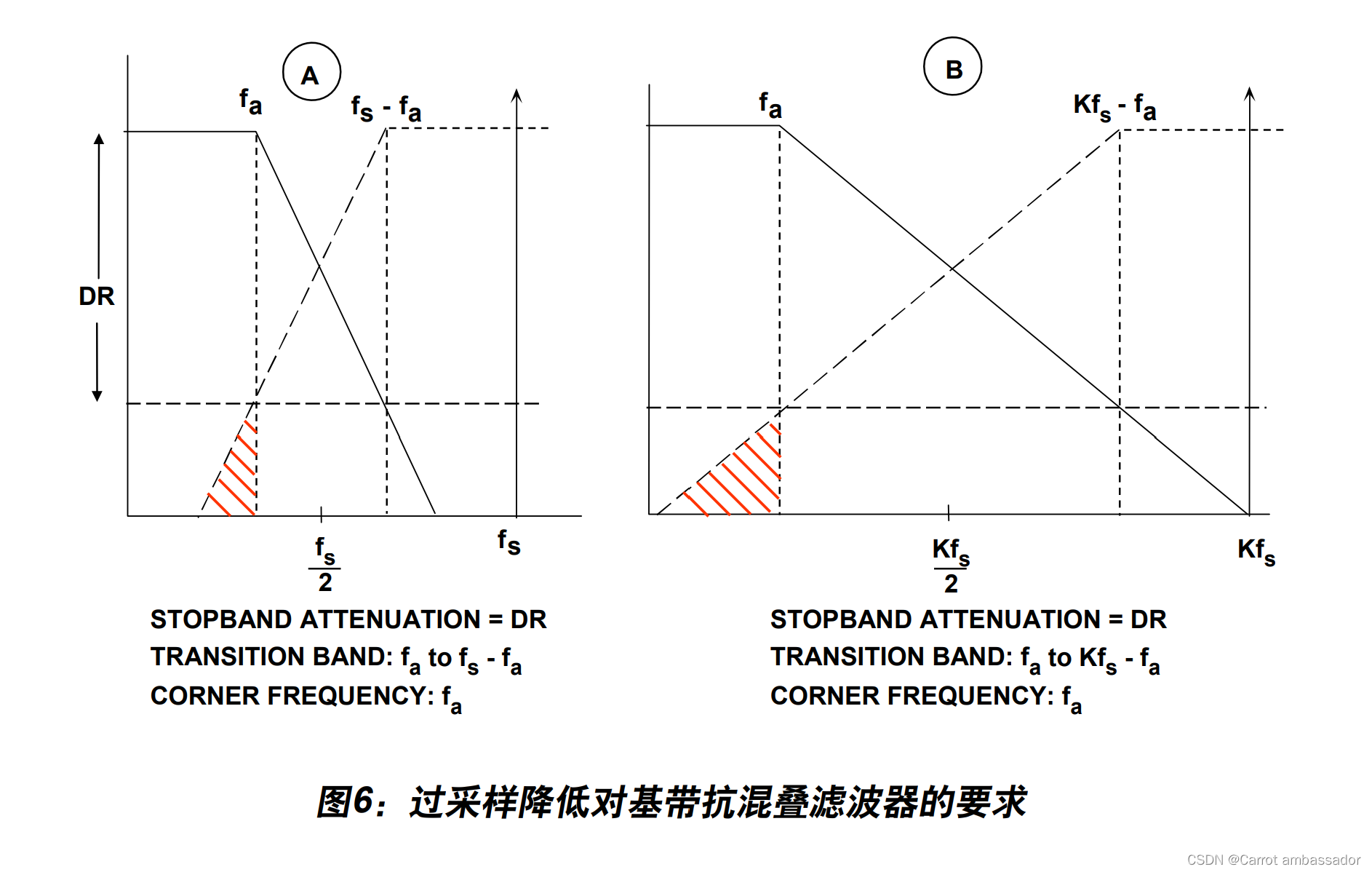
         假定输入信号具有超过最大目标频率fa的满量程成分。该图显示了f s – fa 以上的满量程频率 成分如何混叠回到DC至f a 的带宽范围内。这些混叠成分不易与实际信号区分开来，因此将 动态范围限制为图中显示为DR的值。

         有些文章推荐根据奈奎斯特频率f s /2来指定抗混叠滤波器，但这时假定目标信号带宽为DC 至f s /2，而那种情况非常少见。在图6A的示例中，f a 和f s /2之间的混叠成分并不是目标成 分，因此不会限制动态范围。

         因此，抗混叠滤波器的过渡带取决于转折频率f a 、阻带频率f s – fa 和所需阻带衰减DR。所需 系统动态范围的选择依据是信号保真度要求。

         所有其它条件不变时，过渡带越陡，滤波器就越复杂。例如，与所有其他滤波器一样，巴特沃斯滤波器针对每个滤波器极点提供每倍频程6 dB衰减。要在1 MHz到2 MHz的过渡区 (1倍频程)内实现60 dB衰减，需要至少10个极点。这样的滤波器可不是随随便便就能实现 的，绝对是一项设计挑战。

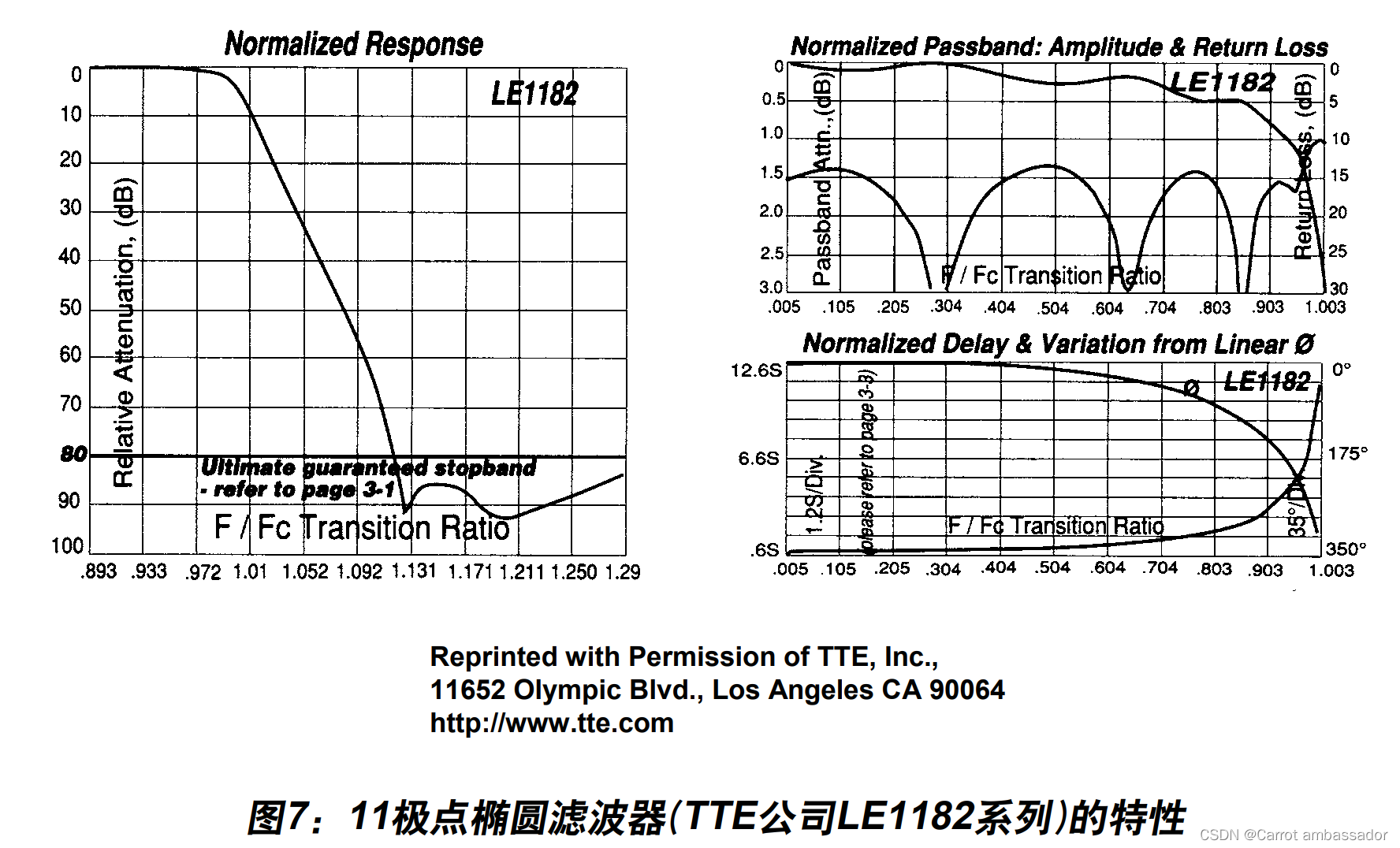
        因此，其它滤波器类型通常更适合于对陡峭过渡带、带内平坦度以及线性相位响应有要求的应用。椭圆滤波器满足这些标准，是一种颇受欢迎的选择。有一些公司专门提供定制模拟滤波器。例如，TTE公司11极点椭圆抗混叠滤波器 LE1182的归一化响应如图7所示。注意，此滤波器专用于在f c 和1.2fc 之间实现至少80 dB衰 减。图7还显示了相应的通带纹波、回损、延迟和相位响应。

        从上述讨论中，我们可以看到如何对抗混叠过渡带的锐度与ADC采样频率作出权衡。选择较高的采样速率(过采样)时，过渡带的锐度要求有所降低(因而滤波器复杂程度也相应降 低)，但是需要使用更快的ADC，并且需要以更快的速率来处理数据。图6B显示了保持模 拟转折频率f a 和动态范围DR要求不变但采样频率调高K倍时所产生的影响。对于图6A中的 情况，过渡带(f a 至Kfs – fa )越宽，那么此过滤器设计就越简单。

        抗混叠滤波器设计过程从选择大小等于2.5到4倍f a 的初始采样速率开始。接着，根据所需动态范围确定滤波器规格并判断是否可在系统成本和性能限制范围内实现该滤波器。如果 无法实现，则考虑使用较高的采样速率，而这可能要求使用更快的ADC。值得一提的是， Σ-Δ型ADC本质上属于高过采样转换器，因此此架构又添一项优势，那就是可以降低对模 拟抗混叠滤波器的要求。

        如果确定永远不会出现阻带频率f s – fa 的满量程信号，也可降低对抗混叠滤波器的要求。很 多应用中都不太可能会出现此频率的满量程信号。如果f s – fa 频率的最大信号永远不会超过满量程以下X dB，那么滤波器阻带衰减要求也会出现同幅下降。基于对信号的这种了解， f s – fa 处的新阻带衰减要求现在仅为DR – X dB。作出此类假定时，注意要将可能超过最大信号频率f a 的任何噪声信号视作也会叠加回到信号带宽内的干扰信号。 

3、欠采样(谐波采样、带通采样、中频采样、直接中频数字转换)

         到目前为止，我们考虑的是基带采样情况，即所有目标信号均位于第一奈奎斯特区内。图 8A显示了另外一种情况，其中采样信号频带局限于第一奈奎斯特区，而原始频带镜像出现在其它每个奈奎斯特区。 以图8B所示的情况为例，其中采样信号频带完全位于第二奈奎斯特区内。对第一奈奎斯特区之外的信号进行采样的过程通常称为“欠采样”或“谐波采样”。注意，第一奈奎斯特区内的镜像包含原始信号中的所有信息，但其原始位置除外(频谱内频率成分的顺序是相反 的，但这点可轻松地通过重新调整FFT输出的顺序来加以纠正)

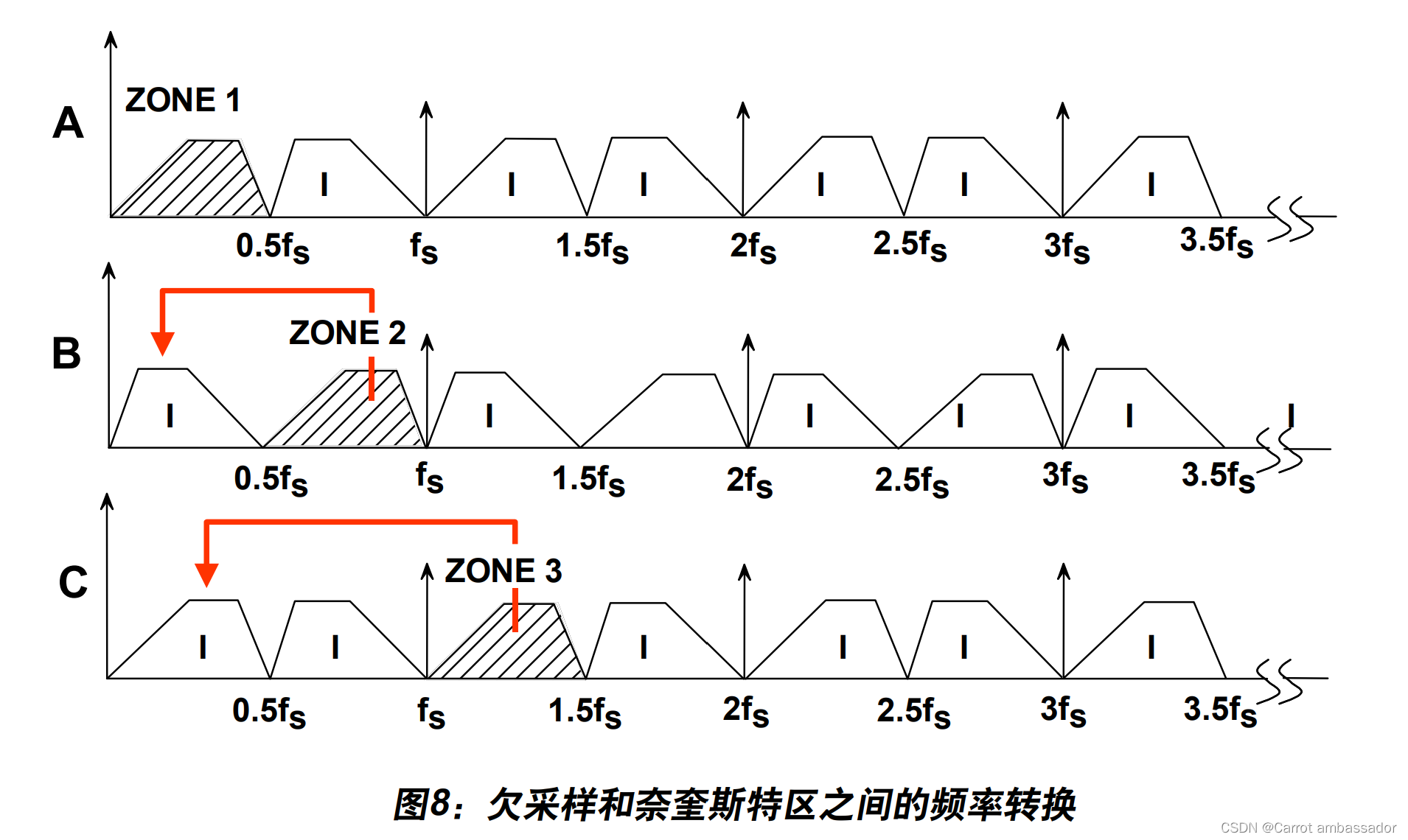
         图8C显示了限制至第三奈奎斯特区的采样信号。注意，第一奈奎斯特区内的镜像并未频 谱反转。实际上，采样信号频率可能位于任意独特的奈奎斯特区内，而第一奈奎斯特区内 的镜像仍旧是精确表示(当信号位于编号为偶数的奈奎斯特区时出现的频谱反转除外)。此 时，我们可以重提奈奎斯特准则，因为其适用于宽带信号：带宽为BW的信号必须以等于或大于其带宽两倍(2BW)的速率进行采样，方可保留信号中的全部信息。

         注意，该处并没有提到采样信号频带相对于采样频率在频谱内的绝对位置。唯一的限制是 采样信号频带必须局限于单个奈奎斯特区，即信号不得重叠任意多个f s /2(实际上，这就是 抗混叠滤波器的主要功能)。

         在通信应用中，对第一奈奎斯特区以上的信号进行采样等效于模拟解调，因此越来越受欢 迎。直接对中频信号进行采样，然后使用数字技术来处理该信号，这种做法已经日渐普 遍，从而不再需要中频解调器和滤波器。不过显然，IF频率越高，对ADC的动态性能要求 就越严格。ADC输入带宽和失真性能必须足以处理IF频率，而不仅仅是基带。这就给仅设 计用来处理第一奈奎斯特区内信号的大多数ADC带来了一项难题——适合欠采样应用的 ADC必须在高阶奈奎斯特区内保持动态性能不变。

4、欠采样应用中的抗混叠滤波器

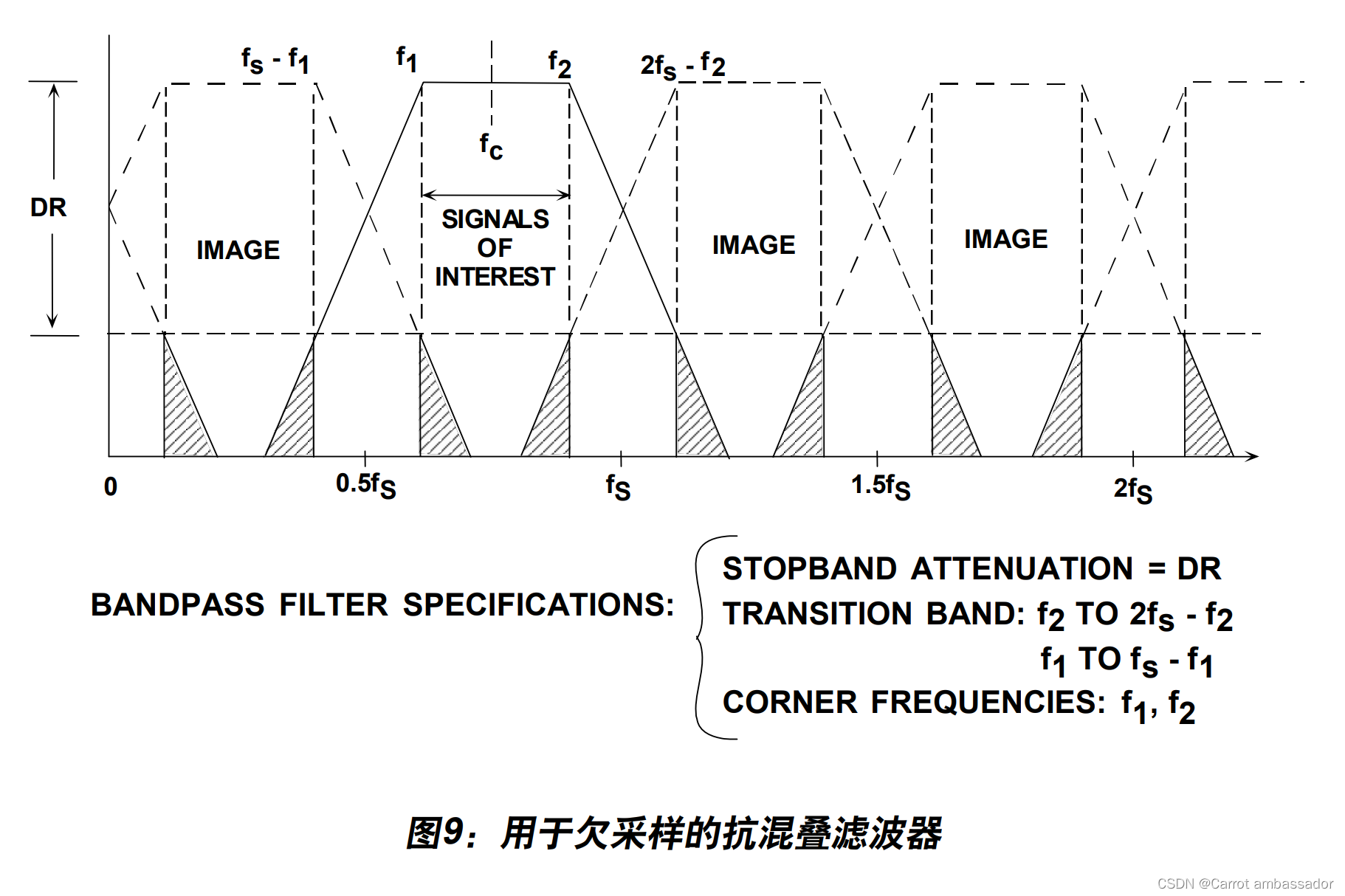
         图9显示了以载波频率f c 为中心的第二奈奎斯特区内的信号，其中频率下限和上限分别为f 1 和f 2 。抗混叠滤波器是一个带通滤波器。所需动态范围为DR，该范围定义了滤波器阻带衰减。过渡带上限为f 2 至2fs – f2 ，而下限则为f 1 至f s – f1 。对于基带采样，通过按比例调高采样 频率可以降低对抗混叠滤波器的要求，但还必须改变f c ，使其始终是第二奈奎斯特区的中心。

         给定载波频率f c 及其信号带宽Δf时，可使用两个关键等式来选择采样频率f s 。首先是奈奎斯 特准则：

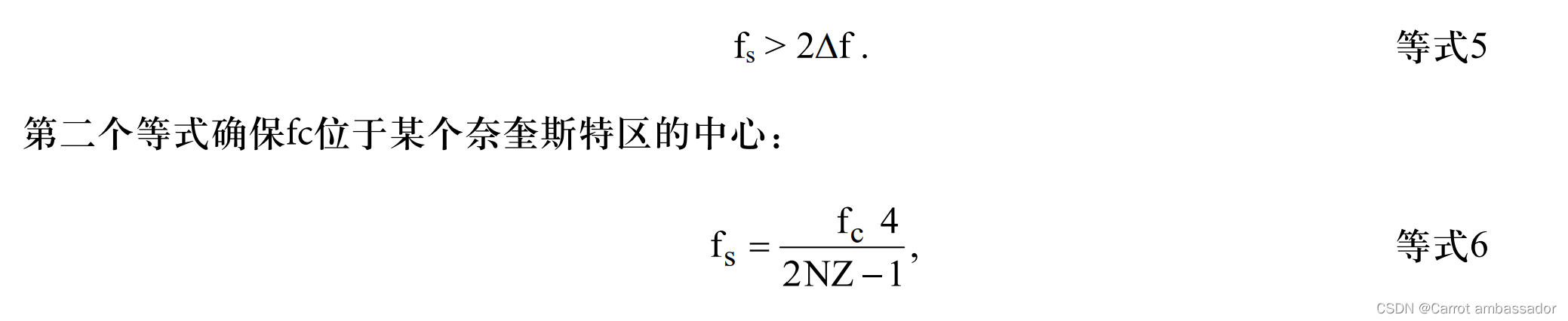
         其中，NZ = 1, 2, 3, 4, ....，且NZ对应于载波及其信号所位于的奈奎斯特区(见图10)。

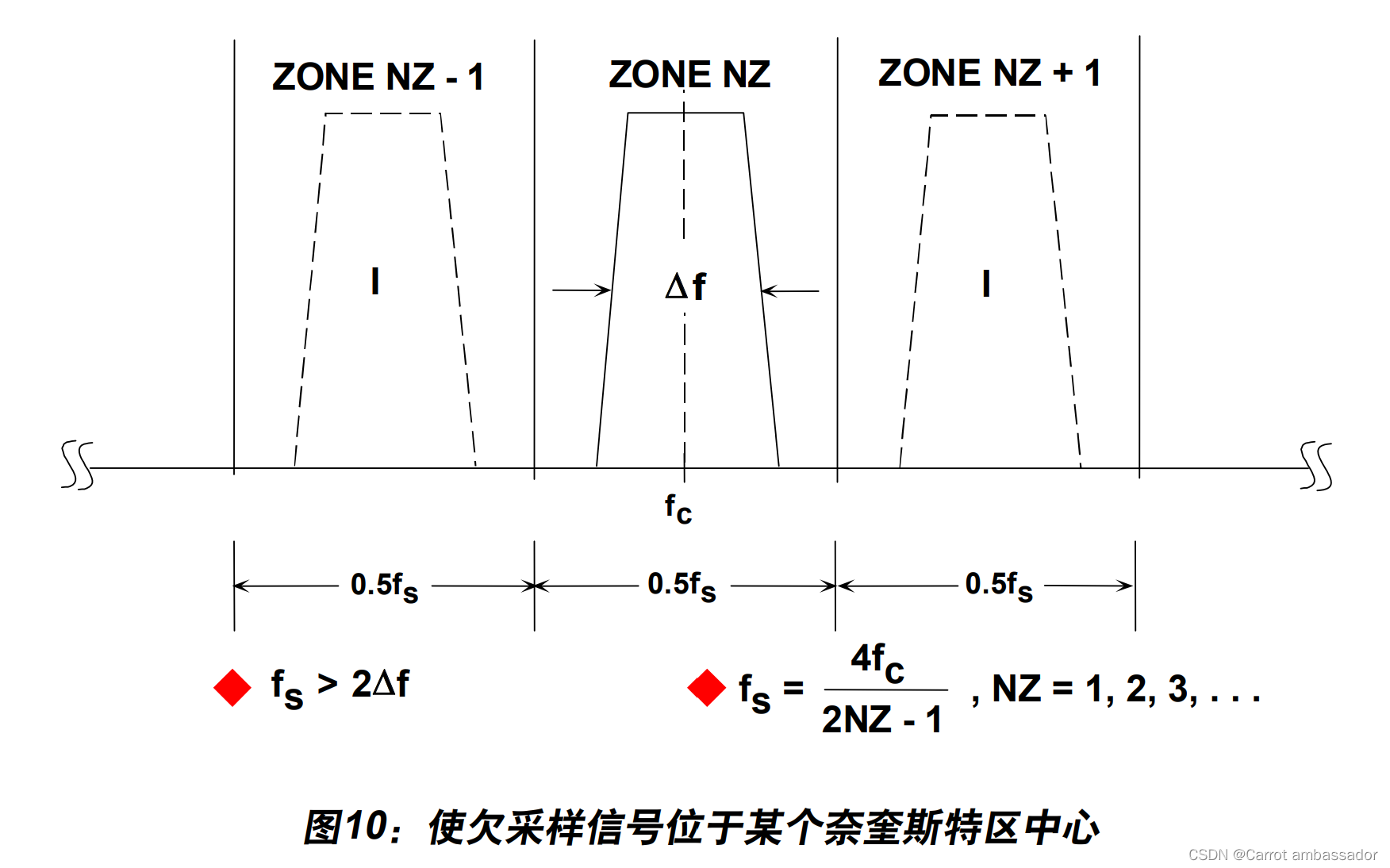
        一般而言，NZ越大越好，从而允许处理高IF频率。无论NZ选择多少，奈奎斯特准则都要 求f s > 2Δf。如果NZ选择为奇数，那么f c 及其信号将位于编号为奇数的奈奎斯特区内，而第 一奈奎斯特区内的镜像频率不会反转。

         举例来说，假定信号以载波频率71 MHz为中心且宽度为4 MHz。因此，最低采样频率要求为8 MSPS。通过将f c = 71 MHz和f s = 8 MSPS代入等式6来求解NZ，可得到NZ = 18.25。不过，NZ必须为整数，因此我们把18.25四舍五入为最接近的整数，即18。再次通过等式6来 求解f s ，可得到f s = 8.1143 MSPS。因此，最后的值为f s = 8.1143 MSPS、f c = 71 MHz、NZ = 18 。

        现在假定我们需要抗混叠滤波器具有更多余量，因此将fs选择为10 MSPS。通过将f c = 71 MHz和f s = 10 MSPS代入等式6来求解NZ，可得到NZ = 14.7。我们将14.7四舍五入为最接近的整数，即可得到NZ = 14。再次通过等式6来求解f s ，可得到f s = 10.519 MSPS。因此，最后的值为f s = 10.519 MSPS、f c = 71 MHz、NZ = 14。上述迭代过程也可通过从f s 开始并调整载波频率来为NZ产生一个整数。

--来源ADI《奈奎斯特准则对数据采样系统设计有何意义》，全文没一句废话

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！