GMM和EM算法详解

混合高斯模型和EM算法

一、单个一维高斯参数学习

  数据集X={ x 1 , x 2 . . . . . . . x N x_1,x_2.......x_N x1​,x2​.......xN​},参数为θ={μ， σ 2 σ^2 σ2},图像为：

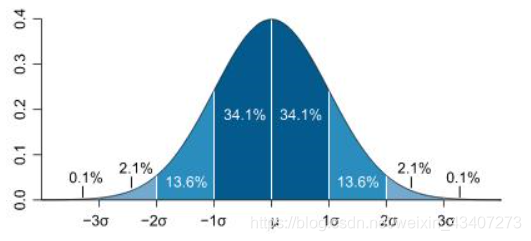
  一维高斯函数的分布如下所示：

p ( x ) = 1 2 π σ e x p ( 1 2 σ 2 ( x − μ ) 2 ) (1.1) \begin{aligned} p(x)=\frac{1}{\sqrt {2π}σ}exp(\frac{1}{2σ^2}(x-μ)^2) \tag{1.1}\\ \end{aligned} p(x)=2π ​σ1​exp(2σ21​(x−μ)2)​(1.1)

  我们通过极大似然法来求解高斯分布的参数θ,即μ和 σ 2 σ^2 σ2。

  我们可以通过数据集直接得到log似然函数：

P ( X ∣ θ ) = ∑ i = 1 N l o g 1 2 π σ e x p ( 1 2 σ 2 ( x i − μ ) 2 ) = ∑ i = 1 N ( − 1 2 l o g ( 2 π ) − l o g σ − 1 2 σ 2 ( x i − μ ) 2 ) (1.2) \begin{aligned} P(X|θ)=&\displaystyle\sum_{i=1}^{N} log\frac{1}{\sqrt {2π}σ}exp(\frac{1}{2σ^2}(x_i-μ)^2) \\ &=\displaystyle\sum_{i=1}^{N} (-\frac{1}{2}log(2π)-logσ-\frac{1}{2σ^2}(x_i-μ)^2)\tag{1.2} \end{aligned} P(X∣θ)=​i=1∑N​log2π ​σ1​exp(2σ21​(xi​−μ)2)=i=1∑N​(−21​log(2π)−logσ−2σ21​(xi​−μ)2)​(1.2)

  得到了对数似然函数的表达式，我们就可以根据求导为零得到函数的最优解，并且解出参数的最优值。

  例：我们这边求一个μ。

∂ P ( X ∣ θ ) ∂ μ = ∑ i = 1 N ( x i − μ ) = 0 (1.3) \begin{aligned} \frac{\partial P(X|θ)}{\partial μ}=\displaystyle\sum_{i=1}^{N}(x_i-μ)=0 \tag{1.3}\\ \end{aligned} ∂μ∂P(X∣θ)​=i=1∑N​(xi​−μ)=0​(1.3)

  解出

μ = ∑ i = 1 N x i N (1.4) \begin{aligned} μ=\frac{\displaystyle\sum_{i=1}^{N}x_i}{N} \tag{1.4}\\ \end{aligned} μ=Ni=1∑N​xi​​​(1.4)

  数据集X={ x 1 , x 2 . . . . . . . x N x_1,x_2.......x_N x1​,x2​.......xN​},参数为θ={μ，$\Sigma$},图像为：

  我这边只给出2维的高斯分布图，再高维的不能进行可视化了

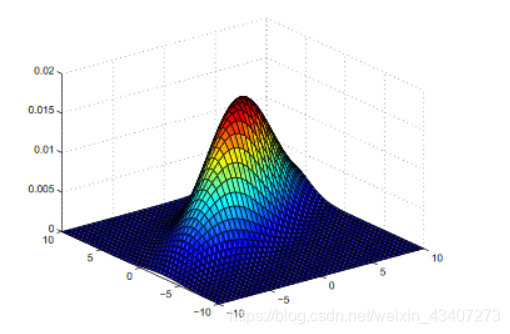
  D维高斯函数的分布如下所示：

p ( x ) = 1 ( 2 π ) D 2 ∣ Σ ∣ 1 2 e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) (2.1) \begin{aligned} p(x)=\frac{1}{(2π)^\frac{D}{2}|\Sigma|^\frac{1}{2}}exp(-\frac{1}{2}(x-μ)^T\Sigma^{-1}(x-μ)) \tag{2.1}\\ \end{aligned} p(x)=(2π)2D​∣Σ∣21​1​exp(−21​(x−μ)TΣ−1(x−μ))​(2.1)

  我们通过极大似然法来求解高斯分布的参数θ,即μ和$\Sigma$。

  首先写出似然函数：

P ( X ∣ θ ) = ∏ i = 1 N p ( x i ∣ θ ) \begin{aligned} P(X|θ)=\displaystyle\prod_{i=1}^{N} p(x_i|θ) \end{aligned} P(X∣θ)=i=1∏N​p(xi​∣θ)​

  他所对应的对数似然函数为：

P ( X ∣ θ ) = ∑ i = 1 N l o g p ( x i ∣ θ ) (2.2) \begin{aligned} P(X|θ)=\displaystyle\sum_{i=1}^{N} logp(x_i|θ) \tag{2.2}\\ \end{aligned} P(X∣θ)=i=1∑N​logp(xi​∣θ)​(2.2)

  我们将一维高斯密度函数带入对数似然函数中可以得到

P ( X ∣ θ ) = ∑ i = 1 N l o g 1 ( 2 π ) D 2 ∣ Σ ∣ 1 2 e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) = ∑ i = 1 N ( − D 2 l o g ( 2 π ) − 1 2 l o g ∣ Σ ∣ − 1 2 ( ( x i − μ ) T Σ − 1 ( x i − μ ) ) (2.3) \begin{aligned} P(X|θ)=&\displaystyle\sum_{i=1}^{N} log\frac{1}{(2π)^\frac{D}{2}|\Sigma|^\frac{1}{2}}exp(-\frac{1}{2}(x-μ)^T\Sigma^{-1}(x-μ))\\ &=\displaystyle\sum_{i=1}^{N} (-\frac{D}{2}log(2π)-\frac{1}{2}log|\Sigma|-\frac{1}{2}((x_i-μ)^T\Sigma^{-1}(x_i-μ)) \tag{2.3}\\ \end{aligned} P(X∣θ)=​i=1∑N​log(2π)2D​∣Σ∣21​1​exp(−21​(x−μ)TΣ−1(x−μ))=i=1∑N​(−2D​log(2π)−21​log∣Σ∣−21​((xi​−μ)TΣ−1(xi​−μ))​(2.3)

  得到了对数似然函数的表达式，我们就可以根据求导为零得到函数的最优解，并且解出参数的最优值。

  例：我们这边求一个μ。

∂ P ( X ∣ θ ) ∂ μ = ∑ i = 1 N ( x i − μ ) = 0 (2.4) \begin{aligned} \frac{\partial P(X|θ)}{\partial μ}=\displaystyle\sum_{i=1}^{N}(x_i-μ)=0 \tag{2.4}\\ \end{aligned} ∂μ∂P(X∣θ)​=i=1∑N​(xi​−μ)=0​(2.4)
  解出

μ = ∑ i = 1 N x i N (2.5) \begin{aligned} μ=\frac{\displaystyle\sum_{i=1}^{N}x_i}{N} \tag{2.5}\\ \end{aligned} μ=Ni=1∑N​xi​​​(2.5)

三、混合高斯模型

  混合高斯模型就是类似于一个聚类算法，他不仅考虑了数据的均值，也考虑了数据的协方差，所以说它是属于无监督学习的范畴，不需要类标签。它是由K个高斯模型混合而成，比如说对于下面的这张数据图：

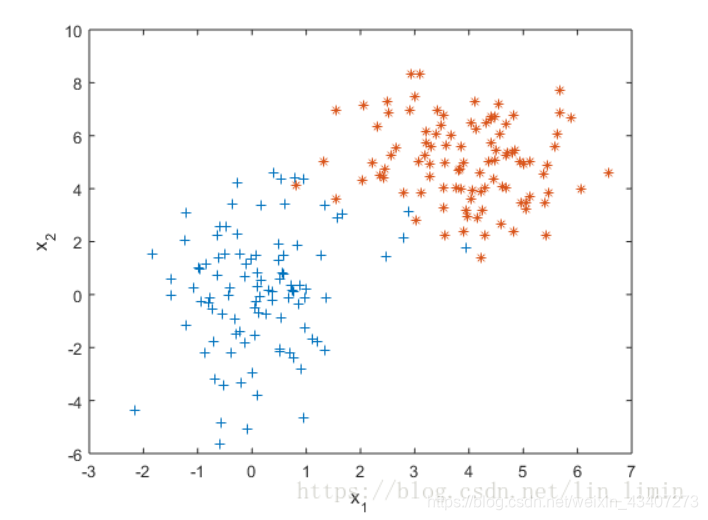
  我们可以看出，它并不能只由单一的高斯分布来表示，所以我们引入了混合高斯模型，他将K个高斯模型进行加权求和来表示。理论上来说，只要K足够大，那么混合高斯就可以拟合任意的曲线，或者空间。

  下面我们就开始对高斯混合模型进行详细的阐述：

  首先，数据集X同样为{ x 1 , x 2 . . . . . . . x N x_1,x_2.......x_N x1​,x2​.......xN​},但是，我们这边的参数相对于之前的单一模型要多出来一个权重 π i π_i πi​,所以整个参数空间为

θ = ( μ 1 , μ 2 , , , , μ k , Σ 1 , Σ 2 , , , , Σ k , π 1 , π 2 , , , , π k ) \begin{aligned} θ=(μ_1,μ_2,,,,μ_k,\Sigma_1,\Sigma_2,,,,\Sigma_k,π_1,π_2,,,,π_k)\\ \end{aligned} θ=(μ1​,μ2​,,,,μk​,Σ1​,Σ2​,,,,Σk​,π1​,π2​,,,,πk​)​

  我们先写出单个高斯的一个分布函数
p ( x ) = N ( x ∣ μ i , Σ i ) = 1 ( 2 π ) D 2 ∣ Σ i ∣ 1 2 e x p ( − 1 2 ( x − μ i ) T Σ i − 1 ( x − μ i ) ) (3.1) \begin{aligned} p(x)=N(x|μ_i,\Sigma_i)=\frac{1}{(2π)^\frac{D}{2}|\Sigma_i|^\frac{1}{2}}exp(-\frac{1}{2}(x-μ_i)^T\Sigma_i^{-1}(x-μ_i)) \tag{3.1}\\ \end{aligned} p(x)=N(x∣μi​,Σi​)=(2π)2D​∣Σi​∣21​1​exp(−21​(x−μi​)TΣi−1​(x−μi​))​(3.1)

  接下来我们就可以写出模型的对数似然函数(log-likehood function)
P ( X ∣ θ ) = l o g ∑ i = 1 K π i N ( X ∣ μ i , Σ i ) = l o g ∑ i = 1 K ∏ j = 1 N π i N ( x j ∣ μ i , Σ i ) = ∑ j = 1 N l o g ∑ i = 1 K π i N ( x j ∣ μ i , Σ i ) (3.2) \begin{aligned} P(X|θ)=&log\displaystyle\sum_{i=1}^{K}\pi_iN(X|μ_i,\Sigma_i)\\ &=log\displaystyle\sum_{i=1}^{K}\displaystyle\prod_{j=1}^{N}\pi_iN(x_j|μ_i,\Sigma_i)\\ &=\displaystyle\sum_{j=1}^{N}log\displaystyle\sum_{i=1}^{K}\pi_iN(x_j|μ_i,\Sigma_i)\\ \tag{3.2}\\ \end{aligned} P(X∣θ)=​logi=1∑K​πi​N(X∣μi​,Σi​)=logi=1∑K​j=1∏N​πi​N(xj​∣μi​,Σi​)=j=1∑N​logi=1∑K​πi​N(xj​∣μi​,Σi​)​(3.2)

  其中 π i \pi_i πi​代表的是每一个样本 x i x_i xi​属于第k个高斯分布的一个概率，并且这k个概率的和应该为1. μ i , Σ i μ_i,\Sigma_i μi​,Σi​为第$i$个高斯分布的均值和协方差。

  我们根据混合高斯分布的似然函数可以知道，要计算它的极大似然通过求导的方式显然是不现实的（由于log函数中存在求和符号），所以我们引入了一种迭代的思想，通过对参数的多次迭代，我们可以渐渐的逼近似然函数的最值。

四、EM算法详解

  EM算法又叫做期望最大化算法，它由两步组成，第一步求期望Q，第二步将期望Q最大化。

E—step:

Q ( θ , θ t ) = ∫ Z P ( X , Z ∣ θ ) ∗ P ( Z ∣ X , θ t ) d ( Z ) (3.3) \begin{aligned} Q(\theta,\theta^t)=\int_ZP(X,Z|\theta)*P(Z|X,\theta^t)d(Z) \tag{3.3}\\ \end{aligned} Q(θ,θt)=∫Z​P(X,Z∣θ)∗P(Z∣X,θt)d(Z)​(3.3)

  其中Z为我们引入的隐变量，在GMM模型中代表的就是每一个样本所在的高斯分布的概率。 θ t \theta^t θt为上一次迭代之后的参数值，是一个确定的值，而$\theta$为变量，在M步中我们需要对Q函数关于$\theta$求最大值。

M—step:

θ t + 1 = a r g m a x Q ( θ , θ t ) (3.5) \begin{aligned} \theta^{t+1}=argmaxQ(\theta,\theta^t) \tag{3.5}\\ \end{aligned} θt+1=argmaxQ(θ,θt)​(3.5)

  下面我们需要证明EM算法对于似然函数来说，在迭代过程中是收敛的。即证明混合高斯模型的$log$似然函数

l o g P ( X ∣ θ t + 1 ) > = l o g P ( X ∣ θ t ) (3.6) \begin{aligned} logP(X|\theta^{t+1})>=logP(X|\theta^t) \tag{3.6}\\ \end{aligned} logP(X∣θt+1)>=logP(X∣θt)​(3.6)

  下面给出证明过程：

l o g P ( X ∣ θ ) = l o g P ( X , Z ∣ θ ) − l o g P ( Z ∣ X , θ ) (3.7) \begin{aligned} logP(X|\theta)=logP(X,Z|\theta)-logP(Z|X,\theta) \tag{3.7}\\ \end{aligned} logP(X∣θ)=logP(X,Z∣θ)−logP(Z∣X,θ)​(3.7)

  将上式两边分别对 P ( Z ∣ X , θ t ) P(Z|X,\theta^t) P(Z∣X,θt)求积分

左 边 = ∫ Z P ( Z ∣ X , θ t ) l o g P ( X ∣ θ ) d Z = l o g P ( X ∣ θ ) ∗ ∫ Z P ( Z ∣ X , θ t ) d Z = l o g P ( X ∣ θ ) (3.8) \begin{aligned} 左边=&\int_ZP(Z|X,\theta^t)logP(X|\theta)dZ\\ &=logP(X|\theta)*\int_ZP(Z|X,\theta^t)dZ\\ &=logP(X|\theta) \tag{3.8}\\ \end{aligned} 左边=​∫Z​P(Z∣X,θt)logP(X∣θ)dZ=logP(X∣θ)∗∫Z​P(Z∣X,θt)dZ=logP(X∣θ)​(3.8)

右 边 = ∫ Z l o g P ( X , Z ∣ θ ) P ( Z ∣ X , θ t ) d Z − ∫ Z l o g P ( Z ∣ X , θ ) P ( Z ∣ X , θ t ) d Z = Q ( θ , θ t ) − H ( θ , θ t ) (3.9) \begin{aligned} 右边=&\int_ZlogP(X,Z|\theta)P(Z|X,\theta^t)dZ-\int_ZlogP(Z|X,\theta)P(Z|X,\theta^t)dZ\\ &=Q(\theta,\theta^t)-H(\theta,\theta^t) \tag{3.9}\\ \end{aligned} 右边=​∫Z​logP(X,Z∣θ)P(Z∣X,θt)dZ−∫Z​logP(Z∣X,θ)P(Z∣X,θt)dZ=Q(θ,θt)−H(θ,θt)​(3.9)

  其中Q就是我们上面提到的期望，H我们后面阐述。
  所以说由上面可以得到

l o g P ( X ∣ θ ) = Q ( θ , θ t ) − H ( θ , θ t ) \begin{aligned} logP(X|\theta)=Q(\theta,\theta^t)-H(\theta,\theta^t) \end{aligned} logP(X∣θ)=Q(θ,θt)−H(θ,θt)​

l o g P ( X ∣ θ t ) = Q ( θ t , θ t ) − H ( θ t , θ t ) (3.10) \begin{aligned} logP(X|\theta^t)=Q(\theta^t,\theta^t)-H(\theta^t,\theta^t) \tag{3.10}\\ \end{aligned} logP(X∣θt)=Q(θt,θt)−H(θt,θt)​(3.10)

l o g P ( X ∣ θ t + 1 ) = Q ( θ t + 1 , θ t ) − H ( θ t + 1 , θ t ) (3.11) \begin{aligned} logP(X|\theta^{t+1})=Q(\theta^{t+1},\theta^t)-H(\theta^{t+1},\theta^t) \tag{3.11}\\ \end{aligned} logP(X∣θt+1)=Q(θt+1,θt)−H(θt+1,θt)​(3.11)

  因为Q函数最大化后参数$\theta$为 θ t + 1 \theta^{t+1} θt+1，所以说

Q ( θ t + 1 , θ t ) > = Q ( θ t , θ t ) \begin{aligned} Q(\theta^{t+1},\theta^t)>=Q(\theta^t,\theta^t) \end{aligned} Q(θt+1,θt)>=Q(θt,θt)​

  所以只要证明 H ( θ t + 1 , θ t ) < = H ( θ t , θ t ) H(\theta^{t+1},\theta^t)<=H(\theta^t,\theta^t) H(θt+1,θt)<=H(θt,θt),我们就可以证明$log$似然函数

l o g P ( X ∣ θ t + 1 ) > = l o g P ( X ∣ θ t ) \begin{aligned} logP(X|\theta^{t+1})>=logP(X|\theta^t) \end{aligned} logP(X∣θt+1)>=logP(X∣θt)​

  下面证明 H ( θ t + 1 , θ t ) < = H ( θ t , θ t ) H(\theta^{t+1},\theta^t)<=H(\theta^t,\theta^t) H(θt+1,θt)<=H(θt,θt)，

H ( θ t + 1 , θ t ) − H ( θ t , θ t ) = ∫ Z l o g P ( Z ∣ X , θ t + 1 ) P ( Z ∣ X , θ t ) d Z ∫ Z l o g P ( Z ∣ X , θ t ) P ( Z ∣ X , θ t ) d Z = ∫ Z P ( Z ∣ X , θ t ) l o g P ( Z ∣ X , θ t + 1 ) l o g P ( Z ∣ X , θ t ) d Z (3.12) \begin{aligned} &H(\theta^{t+1},\theta^t)-H(\theta^t,\theta^t)\\ &=\int_ZlogP(Z|X,\theta^{t+1})P(Z|X,\theta^t)dZ\int_ZlogP(Z|X,\theta^t)P(Z|X,\theta^t)dZ\\ &=\int_ZP(Z|X,\theta^t)\frac{logP(Z|X,\theta^{t+1})}{logP(Z|X,\theta^t)}dZ \tag{3.12}\\ \end{aligned} ​H(θt+1,θt)−H(θt,θt)=∫Z​logP(Z∣X,θt+1)P(Z∣X,θt)dZ∫Z​logP(Z∣X,θt)P(Z∣X,θt)dZ=∫Z​P(Z∣X,θt)logP(Z∣X,θt)logP(Z∣X,θt+1)​dZ​(3.12)

  这边我们可以看做是-KL散度，可以证明$-KL<=0$，即 H ( θ t + 1 , θ t ) < = H ( θ t , θ t ) H(\theta^{t+1},\theta^t)<=H(\theta^t,\theta^t) H(θt+1,θt)<=H(θt,θt)成立。

  我们以上我们就证明了EM算法的收敛性，当然我们也可以根据Jesion不等式来证明，在这里就不做过多阐述了。

  接下来我们将EM算法用于GMM模型的参数估计，为什么GMM模型的参数要用EM算法估计在上面我们说明过了。

E—step:

  我们求出$gama[i][j]$矩阵，代表的是第i个数据属于第j个高斯分布的概率，公式如下

g a m a [ i ] [ j ] = N ( x i ∣ μ j , Σ j ) ∑ j = 1 K N ( x i ∣ μ j , Σ j ) (3.13) \begin{aligned} gama[i][j]=\frac{N(x_i|μ_j,\Sigma_j)}{\displaystyle\sum_{j=1}^{K}N(x_i|μ_j,\Sigma_j)} \tag{3.13}\\ \end{aligned} gama[i][j]=j=1∑K​N(xi​∣μj​,Σj​)N(xi​∣μj​,Σj​)​​(3.13)

  其中$gama[i][j]$里面的参数都是在时刻t时的。

  下面我们根据$gama[i][j]$矩阵来更新混合高斯里面的参数

M—step:
  更新 μ j t + 1 \mu_j^{t+1} μjt+1​

μ j t + 1 = ∑ i = 1 N x i g a m a [ i ] [ j ] ∑ i = 1 N g a m a [ i ] [ j ] (3.14) \begin{aligned} \mu_j^{t+1}=\frac{\displaystyle\sum_{i=1}^{N}x_igama[i][j]}{\displaystyle\sum_{i=1}^{N}gama[i][j]} \tag{3.14}\\ \end{aligned} μjt+1​=i=1∑N​gama[i][j]i=1∑N​xi​gama[i][j]​​(3.14)

  更新 Σ j t + 1 \Sigma_j^{t+1} Σjt+1​

Σ j t + 1 = ∑ i = 1 N [ x i − μ j t + 1 ] [ x i − μ j t + 1 ] T g a m a [ i ] [ j ] ∑ i = 1 N g a m a [ i ] [ j ] (3.15) \begin{aligned} \Sigma_j^{t+1}=\frac{\displaystyle\sum_{i=1}^{N}[x_i-\mu_j^{t+1}][x_i-\mu_j^{t+1}]^Tgama[i][j]}{\displaystyle\sum_{i=1}^{N}gama[i][j]} \tag{3.15}\\ \end{aligned} Σjt+1​=i=1∑N​gama[i][j]i=1∑N​[xi​−μjt+1​][xi​−μjt+1​]Tgama[i][j]​​(3.15)

  更新 π j t + 1 \pi_j^{t+1} πjt+1​

π j t + 1 = ∑ i = 1 N N (3.16) \begin{aligned} \pi_j^{t+1}=\frac{\displaystyle\sum_{i=1}^{N}}{N} \tag{3.16}\\ \end{aligned} πjt+1​=Ni=1∑N​​​(3.16)

  所以，这样迭代多次，当极大似然函数的值变化小于某一个阈值后，我们就可以停止迭代，此时参数的值就是极大似然函数的最优解。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！