复信号处理（1）----复信号理解

从某种意义上来说，复信号其实是实信号的一种另类表征，所描述的频带信息减少了重复描述且对称的另外一个边带。

以一幅值梯度变化正弦信号为例，如下图

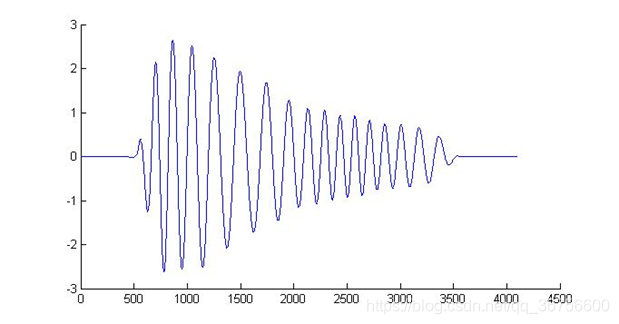
这是我们常规看到的时域信号，信号幅值随时间有规律的变化着，其频谱假定如下所示：

可以看到我们信号在频率轴上有对称的频谱，这两个频谱在频域上变化完全相同。但是却占据了两倍带宽的频谱资源，这最主要的体现就是奈奎斯特定律，AD采样就算是最低的带通采样也得要求采样率不得小于信号带宽的两倍采样率。

于是我们的前辈在研究的过程中就很想通过某种方法，能取得其中一个频谱，以减少后续处理的计算力。如同这样：

在探索的路上，我们的希尔伯特同学则从频域的角度找到了一种好的方案，此方案便叫做希尔伯特变化，为方便理解，此处用一组处理流程来表示：

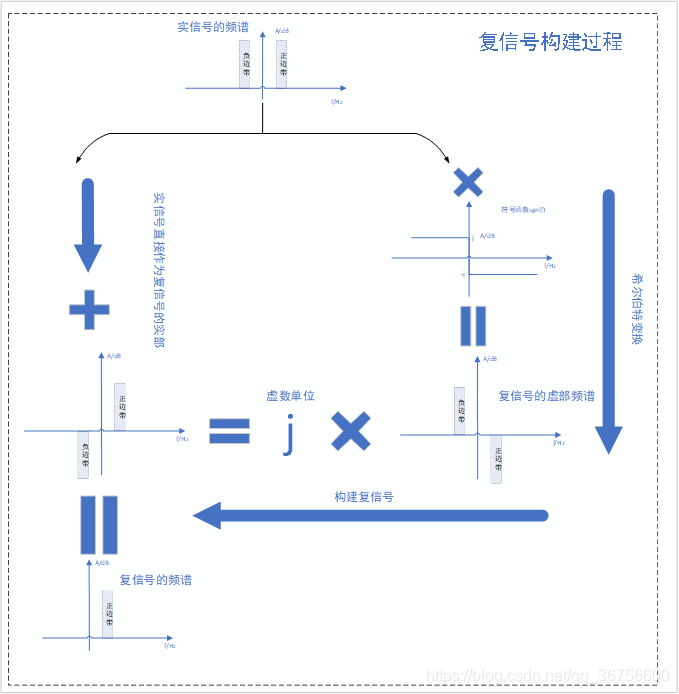
换句话来说，希尔伯特变换就是让实信号的频谱去相乘一组虚部符号函数，这样能构成负边带信号幅值取反，毕竟虚数的平方等于－1，这是一个十分巧妙的办法。最终构建的一个复信号，等效于原实信号和希尔伯特变换构成的虚信号相加，所以表征到时域-二维域（存在虚部，必须引入虚轴才能表示，可以理解为原本一条直线上的变化无法表征一个面的变化）则如下：

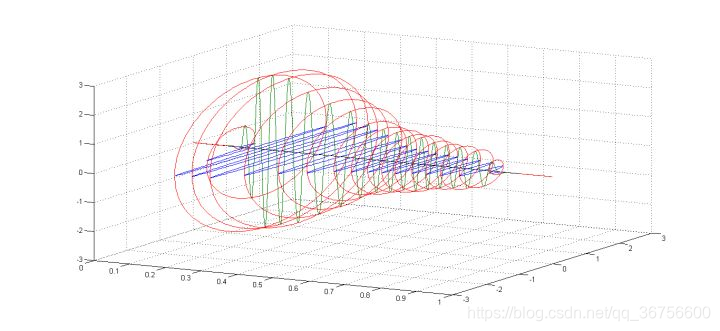
复信号就产生了，其实我有在推测，我们的DNA双链结构也是否存在与此相关：

回归正题：

我们在通过不同角度去观察，也会发现其实复信号的某个投影就是我们的实信号，与虚部构成则是为了抵消负边带的频谱：

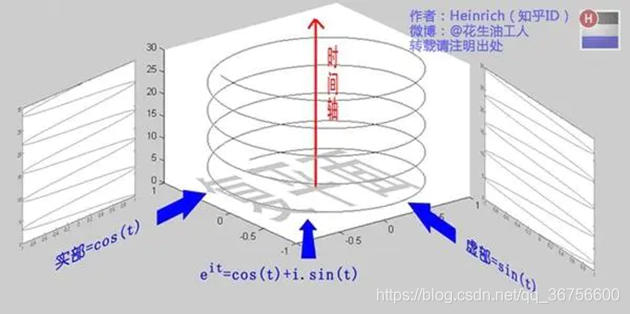
（巴拉的一张照片，主要实在是不想去画图，感谢Heinrich的贡献）

那么问题来了，以上只是给了我们一个理论基础，在实际中，构建一个希尔伯特变换器是很难，乃至几乎不可能（信号相移90度，很难做到一个标准的相移，至于为什么希尔伯特变换也是信号相移，可通过虚符号函数傅里叶逆变换推导可知，在此不做过多讲解）

很开心，我们根据上述理论可以知道一组余弦信号的复信号的虚部表达为正弦信号（相移90度），那么我们很快而且极为标准的余弦复信号频谱表达：

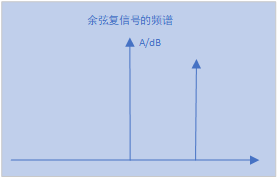
我们让余弦复信号与我们的中心频率对准的实信号几何相乘（有虚部，采用复数乘法运算），时域相乘，频域卷积，根据卷积的原理我们可以知道其结果如下：

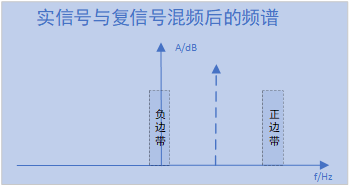
那么我们套一个低通滤波器（实数滤波器即可）就可以获取负边带这个频谱，那么同样也可得到一半频带，如下所示：

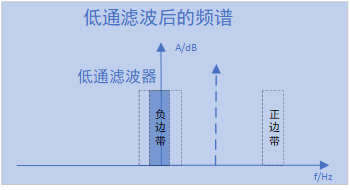
以上流程就是我们经常用到的正交采集，有的叫IQ采样（和IQ解调不同哈，后续会对IQ解调和调制有所讲解），以上得到的结果就是复信号得到常规方式，整个流程如下：

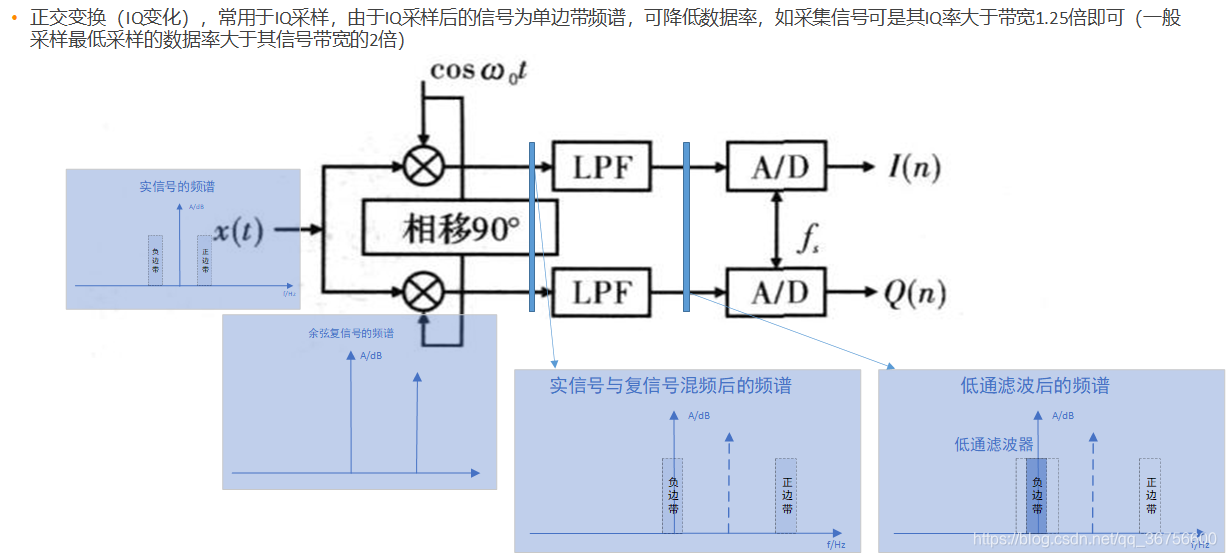
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！