信号处理：＜一＞ 为什么要用复信号

信号处理：<一> 为什么要用复信号

  自己也曾困惑，为什么学习信号处理时总是遇到过很多复信号，实数的不是更容易理解吗？通过查阅资料，自己将自己的理解记录下来。

1、 提高频谱利用率

  以余弦函数为例，提到余弦函数，我们估计都有一个清晰的认识，它的表达式为
x ( t ) = c o s ( ω 0 t ) x(t) = cos(\omega_0t) x(t)=cos(ω0​t)
换个角度，从信号处理的处理的频谱角度看（可以根据傅里叶变化公式求得）
X ( ω ) = ∫ − ∞ ∞ x ( t ) e − j ω t d t X(\omega) = \int_{-\infty}^\infty{x(t)e^{-j\omega t}dt} X(ω)=∫−∞∞​x(t)e−jωtdt
余弦函数的傅里叶变化为：
X ( ω ) = π [ δ ( ω + ω 0 ) + δ ( ω − ω 0 ) ] X(\omega) = \pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)] X(ω)=π[δ(ω+ω0​)+δ(ω−ω0​)]
余弦函数的时域和频域图像为：

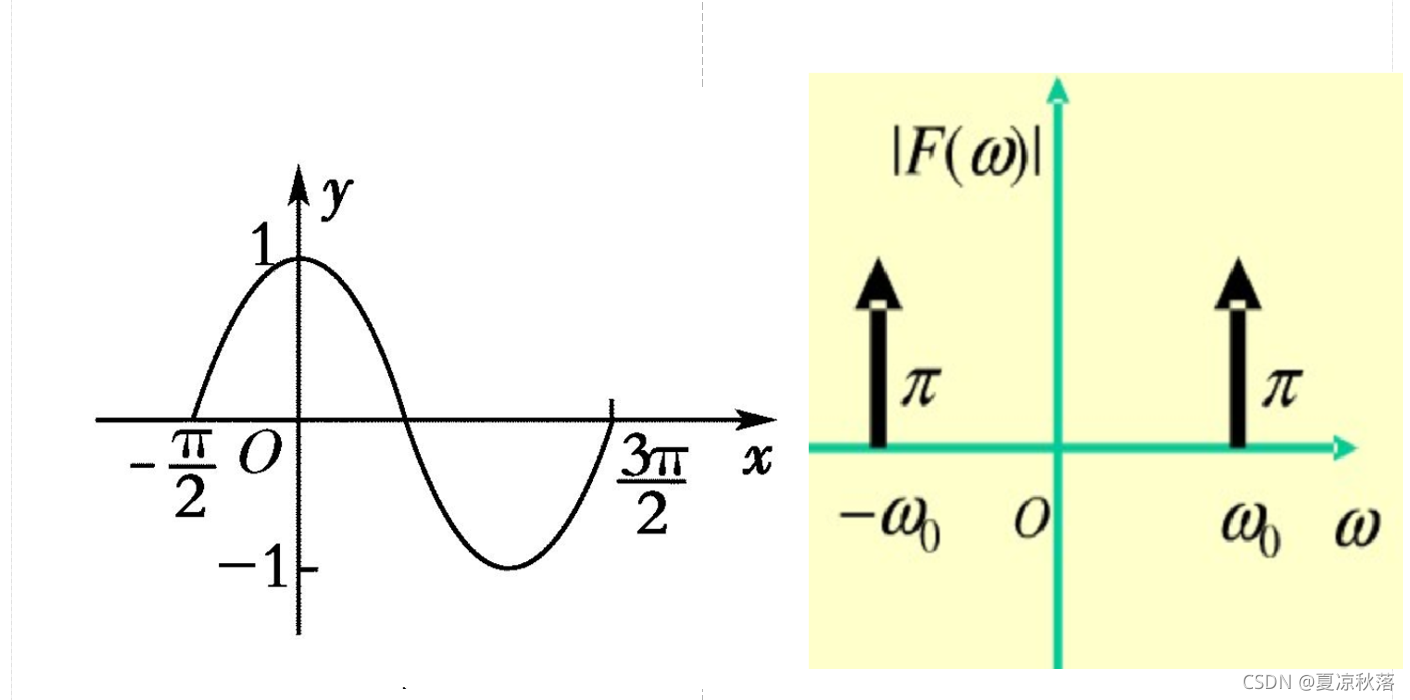
从图中可以看出，余弦（实信号具有共轭对称的频谱 ）信号的频谱谱线有两根（正负谱线），而 从信息的角度来看，其负频谱部分是冗余的，将实信号的负频谱部分去掉，只保留正频谱部分的信号。
对于频谱不存在共轭对称性，所对应的时域信号应为复信号。以 e j ω 0 t e^{j\omega_0 t} ejω0​t为例，由欧拉公式可知，
e j ω 0 t = c o s ( ω 0 t ) + j s i n ( ω 0 t ) e^{j\omega_0 t}=cos(\omega_0 t)+jsin(\omega_0 t) ejω0​t=cos(ω0​t)+jsin(ω0​t)
其对应的傅里叶变换为 2 π δ ( ω − ω 0 ) 2\pi\delta(\omega-\omega_0) 2πδ(ω−ω0​),其频谱只在 ω 0 \omega_0 ω0​有值，而且频谱峰值为$2\pi$,是实信号 c o s ( ω 0 t ) cos(\omega_0t) cos(ω0​t)的2倍。从上面分析可以看出，采用复数信号，提高了频谱利用率。

2、抗混叠

   通信一般具有载波，早期通信的载波为正弦波，通过调制传输信息，发射和接收的都是实信号，接收后要把调制信号从载波里提取出来，通常的做法是 ：将载频变频到零（通称为零中频）。
  我们知道，通常的变频相当于将载频下移，早期的调幅接收机将下移到较低的中频，其目的是方便选择信号和放大，然后通过幅度检波（调幅信号的载波只有幅度受调制）得到所需的低频信号，现代通信信号有各种调制方式，为便于处理， 需要将频带内的信号的谱结构原封不动的下移到零中频 (统称为基带信号)。很显然， 将接收到的实信号直接变到零中频是不行的 ，因为实信号存在共轭对称的双边谱，随着载频的下移，正、负相互接近，到中频小于信号频带一半时，两部分谱就会发生混叠，当中频为零时混叠最严重，使原信号无法恢复，这时应在变频中注意避免正、负谱分量的混叠，正确的获取基带信号【摘自:博客】。具体如下所示：

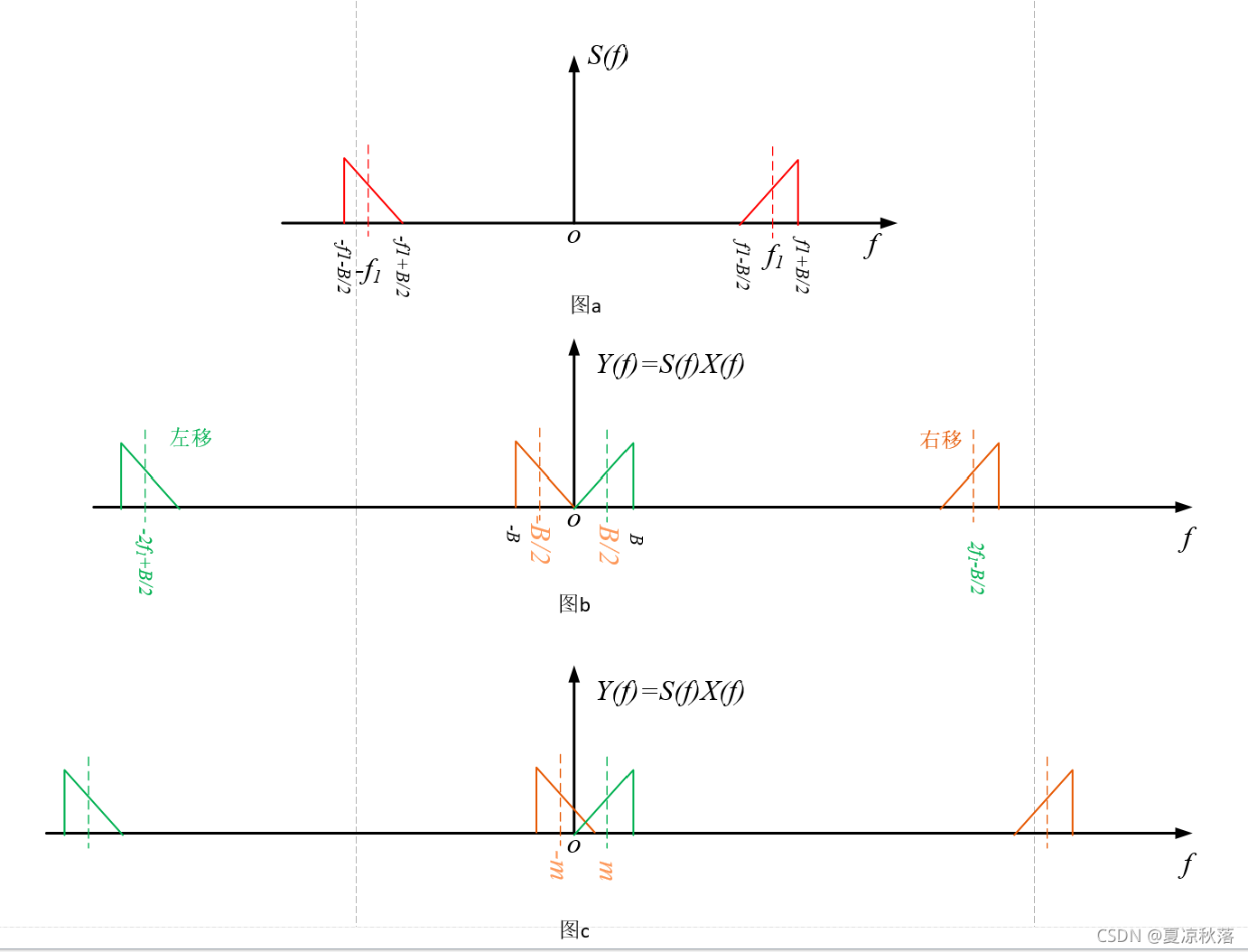
图a为实信号s(t)的频谱，图b为余弦信号频率 f 0 f_0 f0​为 ( f 1 − B / 2 ) (f_1-B/2) (f1​−B/2)或者搬移到信号带宽一半的时候，此时可以搬移后信号的频谱处于重合与不重合的临界状态，此时可以恢复出原始信号。如果在多搬移一段，则正负频率重叠，如图c所示，此时无法恢复出原始信号。
  从数学角度分析上述如下（时域相乘，频域卷积）：
$$时域：y(t)=s(t)x(t)$$
频 率 域 ： Y ( w ) = 1 2 π [ S ( ω ) ∗ X ( ω ) ] = 1 2 [ S ( ω + ω 0 ) + S ( ω − ω 0 ) ] 频率域：Y(w)=\frac{1}{2\pi}[S(\omega)*X(\omega)] =\frac{1}{2}[S(\omega+\omega_0)+S(\omega-\omega_0)] 频率域：Y(w)=2π1​[S(ω)∗X(ω)]=21​[S(ω+ω0​)+S(ω−ω0​)]
其中$\omega =2\pi f$。但如果x(t)为复信号 e j ω 0 t e^{j\omega_0t} ejω0​t,则
Y ( w ) = 1 2 π [ S ( ω ) ∗ X ( ω ) ] = S ( ω − ω 0 ) Y(w)=\frac{1}{2\pi}[S(\omega)*X(\omega)] =S(\omega-\omega_0) Y(w)=2π1​[S(ω)∗X(ω)]=S(ω−ω0​)
此时信号只是单纯向右平移，如果x(t)为复信号 e − j ω 0 t e^{-j\omega_0t} e−jω0​t,则
Y ( w ) = 1 2 π [ S ( ω ) ∗ X ( ω ) ] = S ( ω + ω 0 ) Y(w)=\frac{1}{2\pi}[S(\omega)*X(\omega)] =S(\omega+\omega_0) Y(w)=2π1​[S(ω)∗X(ω)]=S(ω+ω0​)
此时信号单纯向左平移，通过选择合适的参数，可以使信号搬移到基带，当中心频率搬移到零时，带宽会减少一半，会降低AD的采样速率（奈奎斯特定律）。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！