java 椭圆拟合,OpenCV2马拉松第25圈——直线拟合与RANSAC算法
最小二乘法(least square)拟合
Total least square 拟合
RANSAC拟合
葵花宝典
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWJjZDE5OTI3MTln/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="">
终于,我们就能解出B
可是。这样的least square有问题,比方针对垂直线段就不行。于是引入另外一种total least square

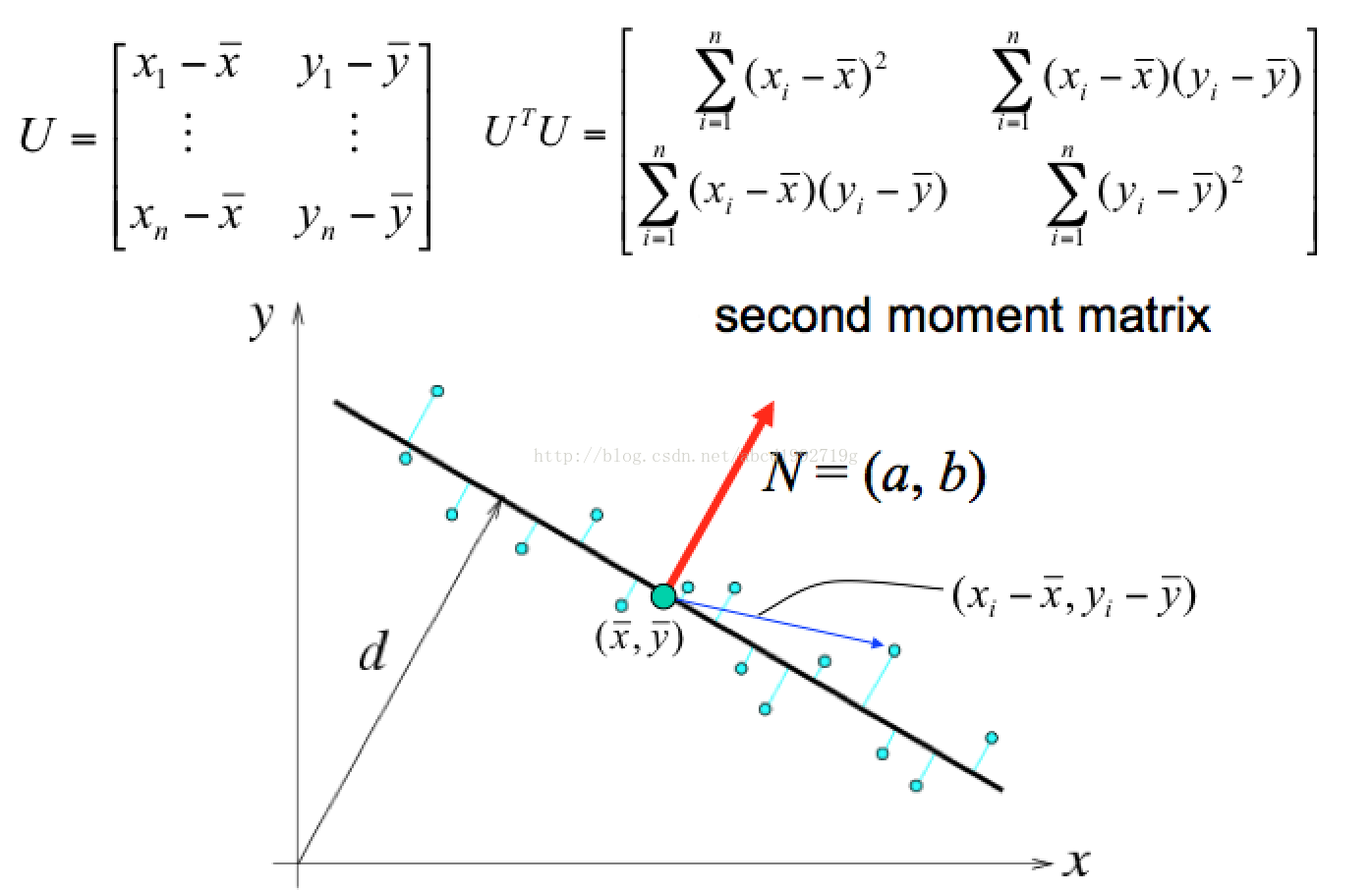
我们能够计算得到N,解出(a,b),然后得到d.
可是误差点对least square的影响非常大。例如以下
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWJjZDE5OTI3MTln/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="">
于是,提出了RANSAC算法
随机在数据集中选出小的子集(对于直线,一般选2)
计算得到符合这个子集合的最好模型
找到接近符合这个模型的数据集
迭代一定次数,选出最好的模型
有图有真相
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWJjZDE5OTI3MTln/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="">
或者參考这里
RANSAC用在直线拟合上。就是
Repeat N times:
•Draws points uniformly at random
•Fit line to theses points
•Find inliers to this line among the remaining points(i.e., points whose distance from the line is less thant)
•If there ared or more inliers, accept the line and refit using all inliers(refit的意思就是:我们迭代后找到了一条最好直线,如果有200个接近点。那么就用这200个点再进行least
square又一次拟合下)
RANSAC是一个概率算法,迭代次数越多越准确
•Pros
•简单通用
•能够解决非常多问题
•实践有效
•Cons
•须要确定一系列參数
•有时候须要迭代次数多。概率算法有时候会失败
•最小样本数无法得到有效模型
初识API
OpenCV提供了一个拟合直线的方法。能够拟合2维和3维空间的直线
C++:void fitLine(InputArray points,
OutputArray line, int distType, double param, double reps, double aeps)
points – 2D或者3D点的输入向量。存储在std::vector<> 或者 Mat中.
line –2D来说 (就像Vec4f) - (vx, vy, x0, y0),(vx, vy)是归一化直线方向,(x0, y0)是直线上的一个点.
对于3D的拟合 (就如 Vec6f) - (vx, vy, vz, x0, y0, z0),
distType – 例如以下
param – 一般取0
reps – 一般取0.01
aeps – 一般取0.01
The function fitLine fits a line to a 2D or 3D point set by minimizing
 where
where
 is
is
a distance between the
 point, the line and
point, the line and
 is
is
a distance function, one of the following:
distType=CV_DIST_L2

distType=CV_DIST_L1

distType=CV_DIST_L12

distType=CV_DIST_FAIR

distType=CV_DIST_WELSCH

distType=CV_DIST_HUBER

荷枪实弹
cv::Vec4f line;
cv::fitLine(cv::Mat(points),line,CV_DIST_L2, 0, 0.01,0.01);
这样调用,就能够得到我们的直线參数
举一反三
cv::fitEllipse 在一系列2D点中拟合椭圆. 它返回一个旋转过的矩形 (一个cv::RotatedRect实例),椭圆内切于这个矩形.
你能够书写例如以下代码:
cv::RotatedRect rrect= cv::fitEllipse(cv::Mat(points));
cv::ellipse(image,rrect,cv::Scalar(0));
函数cv::ellipse用来画出你得到的椭圆
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!