贪心算法 摘要
贪心算法
Date Created: Mar 19, 2021 9:51 AM
Status: 要学习的
贪心算法
严格来说,贪心算法并不是某些有明确指向的算法,而是代指一类算法思想。有多种决策可选时,我们会选择一个最优的策略,即所谓的贪心算法。
- 局部目标:在贪心问题中,总归有一个局部的目标。(先达成一个小目标,之后慢慢影响全局,最终胜利)
- 策略:在这个局部情景里,我们有多种可用的决策。
实际上,很多问题都可以拆解为若干个局部问题和局部策略。如果这一类问题满足:
- 局部问题存在最优解
- 局部问题最优可以保证全局问题最优(怎么看 那么像递归呢?)
满足上述两个条件的话,这个问题就可以通过贪心思想来解决。
小技巧:局部问题又称为子问题,很多复杂的原始问题都可以拆解成若干个子问题构成。例如一盘围棋就可以拆解为每次双方执子的小问题,在不同的情景下,子问题的性质是不一样的,对应的解决办法也是不一样的。
例如:
- 子问题最优则原始问题最优—贪心算法或者动态规则算法
- 子问题最优则原始问题最优,且子问题相互独立—分治算法
- 子问题最优不能推导出原始问题最优—暴力搜索等。
算法中的贪心思想
例1:二叉搜索树找最值
这面先说下二叉搜索树:若它的左子树不空,则左子树上所有的节点的值均小于它的根结点;若它的右子树不空,则右子树上所有的节点点的值均大于它的根结点的值;它的左、右子树也分别为二叉排序树。
在二叉搜索树章节中,有一道题目是要找二叉搜索树的最大/最小值。最初时,假设我们在根节点root。
首先来看子问题:最小值一定在根节点,左节点(如果存在),右子树(如果存在)三者之一上,因此愿问题可以划分为三个子问题。
我们本来可以在左右子树上均查找一次最小值,但是根据二叉查找树的性质,如果左子树存在,那么最小值只可能存在于左子树上。这就是一个贪心的思想,通过只招一边的子树,我们就可以将复杂度从O(n)降至o(log(h)),其中h为树的高度。
例2:二分查找问题
同样,二分查找也存在贪心的思想。再确定l,mid和r后,根据target和mid的大小关系,我们同样只会继续查找左半边或者右半边,这也是因为一边不肯呢个有目标值了。
贪心问题解决思路
那么对于原始的复杂问题,如何能够直到它是否能够被贪心解决呢?
- 首先,我们需要将原始问题拆解成子问题,明确子问题的局面以及局面中可进行的操作。实际上不止贪心问题,很多问题都需要这样的拆解过程。
- 然后我们需要考虑子问题的最优,是否能够保证全局最优。如果能的话,我们就可以只考虑如何解决子问题,否则就可能需要动态规划或者搜索解了。
- 最后,我们需要考虑如何使子问题最优,可能有些问题存在乍一看可行的策略,但是我们仍然需要仔细思考甚至证明。以保证没有漏掉什么细节情况。
小技巧:对于第三点,很多 同学这里会经常犯错。比如以为贪心的做法是对的,但是实际上是有问题的。例如错误的使用贪心解决01背包的问题(子问题最优,愿问题不一定是最优的)等。所以如果我们觉的某道题目存在贪心策略,最好自己证明一下正确性再实现。
分治算法
本章要介绍的另外一种算法是分治算法。前文提到,复杂的原始问题可能可以拆分成若干个子问题,如果子问题之间相互独立(一个子问题的结算结果不依赖其他子问题),那么原始问题可以被分治法解决。
单提概念不容易理解,我们考虑一个具体的场景。假设我们要生产1000件衣服,每条流水线每分钟可以生产一件衣服。那么如果我们有两条流水线,就可以把原始问题拆解为两个生产500件衣服的子问题,总生产时间也就减少为原来的有一半。
所以原始问题是生产1000件衣服,子问题是两个生产500件衣服。子问题各自占用不同的流水线,所以他们相互独立的,因此这是一个分治的思想。
说了这么多,看起来分治就是把一个大问题拆成若干个小问题,最后我们还是得生产1000件衣服,那么分治法究竟有什么作用呢?
- 简化思维逻辑:在很多情况下,原始问题是非常复杂的,例如排序问题。假设原始我们要考虑对1000个数进行排序,那么利用分治思想我们分别对左右的500个数进行排序,然后考虑合并两个有序数组。当然,排序500个数看起来仍然不容易,但是我们可以继续分治下去,最终我们只需要考虑1~2个数的排序策略,这就是经典的归并排序的思想。
- 分布式算法:虽然在算法学习的过程中少有接触多进程和分布式等思想。但随着CPU core越来越多,能够被分治法拆解的问题显然更方便进行并行计算,从而节省总体时间。因此分治思想在工程实现上具有重要的意义。
小知识:在算法的学习过程中,经常有一种声音是质疑学习这些复杂的算法,实际上在工作中没什么作用。但是算法的学习本质上是一个积累和沉淀的过程,一方面我们可以锻炼出更高效和准确的思维和代码实现能力,另一方面在某些场景下也能尝试利用所学内容。比如我们可能会用分治+并行优化执行效率,也可能用分治+线段树优化查找效率。掌握好的算法思想,在某些工作场合能发挥出很大的作用。
- 效率优化:虽让我们不常用并行解决算法问题,但是在某些情况下仍然能够帮助我们节省计算代价,代表就是快速幂算法。
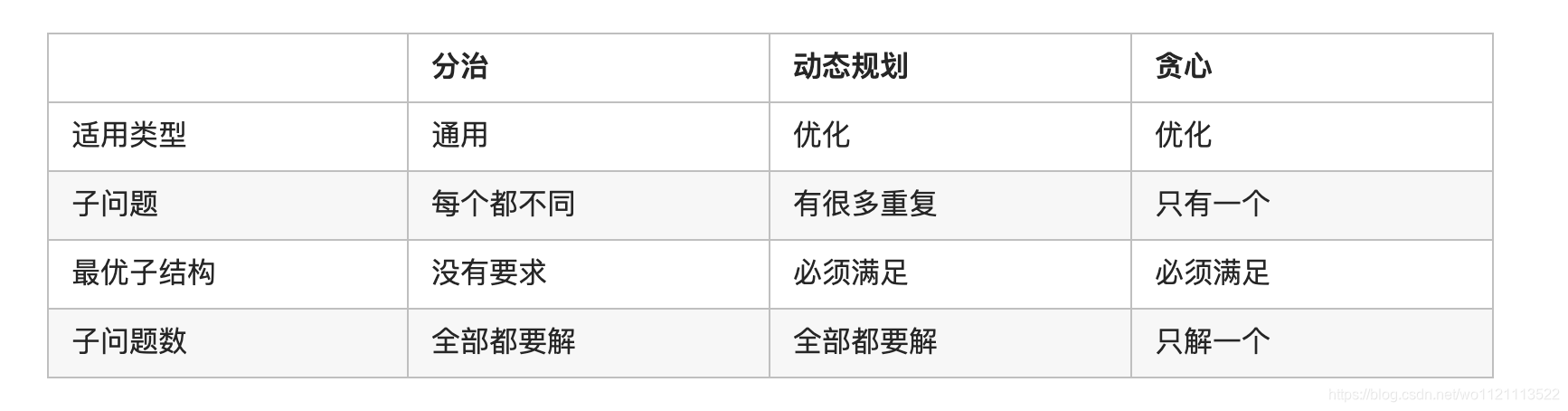
分治算法和贪心算法
总结
- 如果子问题最优则问题最优,贪心算法。
- 如果子问题需要全部求解才能求解原问题,子问题互相独立,分治算法。
- 如果子问题最优不能保证愿问题最优,但是子问题之间不会循环(所谓循环,是指从问题A拆解出子问题B,然后子问题b又能超姐出子问题A),考虑动态规则算法。
- 更加负载的情况,我们总是可以考虑暴力搜索解决。

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!