汉诺塔python递归

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

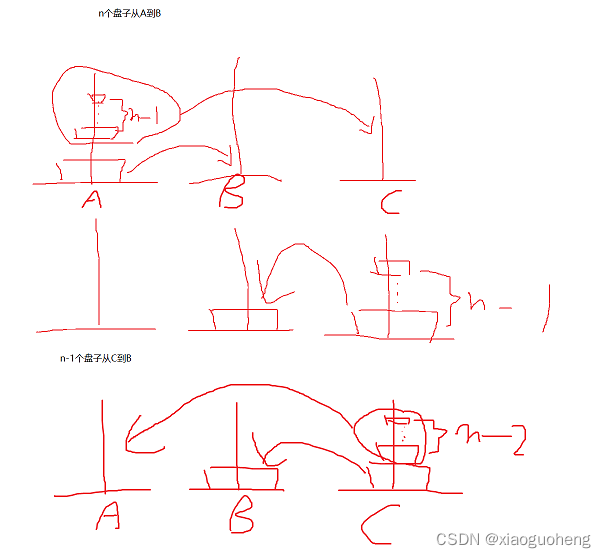
n个盘子从A移到B

1.把前n-1个盘子从A移到C；
2.再把第n个盘子从A移到B；
3.然后把C上的n-1个盘子移到B。

同理，把n-1个盘子从A移动到C

1.把前n-2个盘子从A移到B；
2.再把第n-1个盘子从A移到C；
3.然后把B上的n-1个盘子移到C。

由此看出可以利用递归函数得出过程

def hanoi(n, a, b, c):  # n个盘子从A移动到B借助Cif n > 0:hanoi(n - 1, a, c, b)  # A移动到C借助Bprint('move {} to {}'.format(a, b))hanoi(n - 1, c, b, a)  # C移动到B借助Ahanoi(3, 'A', 'B', "C")

运行结果：

move A to B
move A to C
move B to C
move A to B
move C to A
move C to B
move A to B

汉诺塔移动次数：

h(1) = 1;
h(2) = 3;
...
h(n) = 2h(n-1) + 1；

可算出h(64)=18446744073709551615。假设每秒移动一次，则需要584942417355.072年，大概5800亿年！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！