强化学习：马尔科夫决策中策略迭代、值迭代以及算法实现

文章目录

• • • 1 马尔科夫决策
    • • 1.1 价值函数
      • 1.2 状态价值函数
      • 1.3 动作价值函数
      • 1.4 v π v_\pi vπ​ 和 q π q_\pi qπ​ 的关系
      • 1.5 最优价值函数
      • 1.6 最优策略
    • 2 策略迭代
    • • 2.1 策略评估
      • • 2.1.1 迭代法
      • 2.2 策略改进
      • • 2.2.1 贪心法
      • 2.3 策略迭代算法
    • 3 值迭代
    • 4 租车问题

1 马尔科夫决策

• 状态空间 $S$，动作空间 $A$，状态转移概率 P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a)，奖励函数 R ( s , a , s ′ ) R(s,a,s') R(s,a,s′)，折扣因子 $\gamma \in [0,1]$
• 策略 $\pi (a|s)$，价值函数 v π ( s ) v_\pi(s) vπ​(s)，动作价值函数 q π ( s , a ) q_\pi(s,a) qπ​(s,a)
• $s\in S,a\in A(s),\pi (a|s)\in [0,1]$

1.1 价值函数

G t = ∑ k = 0 ∞ γ k R t + k + 1 = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ (1) G_t = \sum_{k=0}^\infty \gamma^k R_{t+k+1} = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots \tag{1} Gt​=k=0∑∞​γkRt+k+1​=Rt+1​+γRt+2​+γ2Rt+3​+⋯(1)

1.2 状态价值函数

v π ( s ) = E π [ G t ∣ S t = s ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] (2) v_\pi(s) = \mathbb{E}_\pi[G_t|S_t=s] \\ = \mathbb{E}_\pi[\sum_{k=0}^\infty \gamma^k R_{t+k+1}|S_t=s] \\ = \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) \left[r + \gamma v_\pi(s')\right] \tag{2} vπ​(s)=Eπ​[Gt​∣St​=s]=Eπ​[k=0∑∞​γkRt+k+1​∣St​=s]=a∑​π(a∣s)s′,r∑​p(s′,r∣s,a)[r+γvπ​(s′)](2)

1.3 动作价值函数

q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s , A t = a ] = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ ∑ a ′ π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ ) ] (3) q_\pi(s,a) = \mathbb{E}_\pi[G_t|S_t=s,A_t=a] \\ = \mathbb{E}_\pi[\sum_{k=0}^\infty \gamma^k R_{t+k+1}|S_t=s,A_t=a] \\ = \sum_{s',r} p(s',r|s,a) \left[r + \gamma \sum_{a'} \pi(a'|s') q_\pi(s',a')\right] \tag{3} qπ​(s,a)=Eπ​[Gt​∣St​=s,At​=a]=Eπ​[k=0∑∞​γkRt+k+1​∣St​=s,At​=a]=s′,r∑​p(s′,r∣s,a)[r+γa′∑​π(a′∣s′)qπ​(s′,a′)](3)

1.4 v π v_\pi vπ​ 和 q π q_\pi qπ​ 的关系

v π ( s ) = ∑ a π ( a ∣ s ) q π ( s , a ) (4) v_\pi(s) = \sum_a \pi(a|s) q_\pi(s,a) \tag{4} vπ​(s)=a∑​π(a∣s)qπ​(s,a)(4)
q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] (5) q_\pi(s,a) = \sum_{s',r} p(s',r|s,a) \left[r + \gamma v_\pi(s')\right] \tag{5} qπ​(s,a)=s′,r∑​p(s′,r∣s,a)[r+γvπ​(s′)](5)

1.5 最优价值函数

v ∗ ( s ) = max ⁡ π v π ( s ) (6) v_*(s) = \max_\pi v_\pi(s) \tag{6} v∗​(s)=πmax​vπ​(s)(6)
q ∗ ( s , a ) = max ⁡ π q π ( s , a ) (7) q_*(s,a) = \max_\pi q_\pi(s,a) \tag{7} q∗​(s,a)=πmax​qπ​(s,a)(7)

1.6 最优策略

• 存在最优策略 π ∗ \pi_* π∗​，使得 v π ∗ ( s ) ≥ v π ( s ) v_{\pi_*}(s) \geq v_\pi(s) vπ∗​​(s)≥vπ​(s)，即最优策略的价值函数大于等于其他策略的价值函数；
  v π ∗ ( s ) = max ⁡ a q π ∗ ( s , a ) (8) v_{\pi_*}(s) = \max_a q_{\pi_*}(s,a) \tag{8} vπ∗​​(s)=amax​qπ∗​​(s,a)(8)
  即最优状态价值函数等于最优动作价值函数的最大值, 理由是: 任意一个状态，都可以通过任意一个动作到达下一个状态，而下一个状态的价值函数是最优的，所以当前状态的价值函数也是最优的。
• 最优函数之间的关系
  v ∗ ( s ) = max ⁡ a q ∗ ( s , a ) = max ⁡ a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v ∗ ( s ′ ) ] (9) v_*(s) = \max_a q_*(s,a) \\ = \max_a \sum_{s',r} p(s',r|s,a) \left[r + \gamma v_*(s')\right] \tag{9} v∗​(s)=amax​q∗​(s,a)=amax​s′,r∑​p(s′,r∣s,a)[r+γv∗​(s′)](9)
  q ∗ ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ max ⁡ a ′ q ∗ ( s ′ , a ′ ) ] (10) q_*(s,a) = \sum_{s',r} p(s',r|s,a) \left[r + \gamma \max_{a'} q_*(s',a')\right] \tag{10} q∗​(s,a)=s′,r∑​p(s′,r∣s,a)[r+γa′max​q∗​(s′,a′)](10)
  公式(9)和(10)就是贝尔曼方程，是动态规划的基础。

2 策略迭代

• 策略迭代分为两个步骤：策略评估和策略改进。

2.1 策略评估

• 策略评估是指给定一个策略，计算价值函数的过程。
• 策略评估的目标是使得价值函数收敛，即 v π ( s ) → v ∗ ( s ) v_\pi(s) \to v_*(s) vπ​(s)→v∗​(s)，即 v π ( s ) v_\pi(s) vπ​(s) 逼近 v ∗ ( s ) v_*(s) v∗​(s)。
• 策略评估的方法有很多，这里介绍迭代法。

2.1.1 迭代法

• 迭代法是指从一个初始值开始，不断迭代，直到收敛。
• 迭代法的公式如下：
  v k + 1 ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] (11) v_{k+1}(s) = \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) \left[r + \gamma v_k(s')\right] \tag{11} vk+1​(s)=a∑​π(a∣s)s′,r∑​p(s′,r∣s,a)[r+γvk​(s′)](11)
• 算法描述如下：
  • 初始化 v 0 ( s ) = 0 v_0(s) = 0 v0​(s)=0，$k=0$；
  • 计算 v k + 1 ( s ) v_{k+1}(s) vk+1​(s)，$k\leftarrow k+1$；
  • 如果 v k + 1 ( s ) − v k ( s ) < θ v_{k+1}(s) - v_k(s) < \theta vk+1​(s)−vk​(s)<θ，则停止迭代，否则继续迭代。

2.2 策略改进

• 策略改进是指改进策略，使得价值函数更大。
• 策略改进的方法有很多，这里介绍贪心法。

2.2.1 贪心法

• 贪心法是指每次都选择最优的动作，即：
  π ′ ( s ) = arg ⁡ max ⁡ a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] (12) \pi'(s) = \arg\max_a \sum_{s',r} p(s',r|s,a) \left[r + \gamma v_k(s')\right] \tag{12} π′(s)=argamax​s′,r∑​p(s′,r∣s,a)[r+γvk​(s′)](12)

2.3 策略迭代算法

• 策略迭代算法是指不断迭代策略评估和策略改进，直到策略不再改变。
• 一旦一个策略$\pi$根据 v π v_\pi vπ​产生了一个更好的策略 π ′ \pi' π′，那么就可以用 v π ′ v_{\pi'} vπ′​来评估 π ′ \pi' π′，然后再根据 v π ′ v_{\pi'} vπ′​产生一个更好的策略 π ′ ′ \pi'' π′′，以此类推，直到策略不再改变。
• 策略迭代算法的伪代码如下：
  • 初始化 v 0 ( s ) = 0 v_0(s) = 0 v0​(s)=0，$k=0$， π 0 ( s ) = arg ⁡ max ⁡ a q 0 ( s , a ) \pi_0(s) = \arg\max_a q_0(s,a) π0​(s)=argmaxa​q0​(s,a)；
  • 评估策略 π k \pi_k πk​：
    • 计算 v k + 1 ( s ) v_{k+1}(s) vk+1​(s)，$k\leftarrow k+1$；
    • 如果 v k + 1 ( s ) − v k ( s ) < θ v_{k+1}(s) - v_k(s) < \theta vk+1​(s)−vk​(s)<θ，则停止迭代，否则继续迭代；
  • 改进策略 π k \pi_k πk​：
    • π k + 1 ( s ) = arg ⁡ max ⁡ a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] \pi_{k+1}(s) = \arg\max_a \sum_{s',r} p(s',r|s,a) \left[r + \gamma v_k(s')\right] πk+1​(s)=argmaxa​∑s′,r​p(s′,r∣s,a)[r+γvk​(s′)]，$k\leftarrow k+1$；
    • 如果 π k + 1 ( s ) = π k ( s ) \pi_{k+1}(s) = \pi_k(s) πk+1​(s)=πk​(s)，则停止改进，否则继续改进。

3 值迭代

在策略迭代中，策略评估和策略改进是交替进行的，而值迭代则是同时进行的。也就是说，策略评估会提前终止，这并不会影响策略改进的结果。

• 公式如下：
  v k + 1 ( s ) = max ⁡ a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] (13) v_{k+1}(s) = \max_a \sum_{s',r} p(s',r|s,a) \left[r + \gamma v_k(s')\right] \tag{13} vk+1​(s)=amax​s′,r∑​p(s′,r∣s,a)[r+γvk​(s′)](13)
• 值迭代算法的伪代码如下：
  • 初始化 v 0 ( s ) = 0 v_0(s) = 0 v0​(s)=0，$k=0$；
  • 根据公式(13)，计算 v k + 1 ( s ) v_{k+1}(s) vk+1​(s)，$k\leftarrow k+1$；
  • 如果 v k + 1 ( s ) − v k ( s ) < θ v_{k+1}(s) - v_k(s) < \theta vk+1​(s)−vk​(s)<θ，则停止迭代，否则继续迭代。

4 租车问题

• 问题描述：
  杰克管理着一个全国汽车租赁公司的两个地点。每天，一些顾客到每个地点租车。 如果杰克有一辆车可以用来出租，那么他将车租出去并且得到租车公司的10美元报酬。 如果他在这个地点没有车，那么这次生意机会就失去了。汽车被送回来之后就可以被租出去。 为了确保人们需要车子的时候有车可以租，杰克可以在晚上将车子在两个地点之间转移，每转移一辆车需要花费2美元。 我们假设需要车子的数量与返回车子的数量是泊松随机变量，也就是说数量$n$的概率 是 λ n n ! e − λ \frac{\lambda^n}{n!}e^{-\lambda} n!λn​e−λ，$\lambda$是期望值。 假设第一个和第二个地点对于租借需求$\lambda$是3和4，返回数量是3和2。 为了简化问题，我们假设每个位置不会超过20辆车（任何多余的车都将会被返回租赁公司，从问题中消失）， 并且最多五辆车可以在同一晚上从一个地点转移到另一个地点。 我们将衰减因子设置为 $\gamma$=0.9，将这个问题当作连续有限MDP，时间步骤是天数， 状态是每天结束是在每个位置剩余车子的数量，动作是每晚将车子在两个地点转移的净数量。求出最优策略。

• 问题分析：

  • 状态空间： 状态$S$分为两个部分，第一个部分是第一个地点的车辆数目，第二个部分是第二个地点的车辆数目。每个地点的车辆数目都是0到20，所以状态空间是 S = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 } 2 S = \{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\}^2 S={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}2。

  • 动作空间： A = { − 5 , − 4 , − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 , 4 , 5 } A = \{-5,-4,-3,-2,-1,0,1,2,3,4,5\} A={−5,−4,−3,−2,−1,0,1,2,3,4,5}，即每个地点的车辆数目都是0到20。

  • 设每个地点的车辆数目为随机变量$s$, 下一个状态为 s ′ s' s′, 租车数为随机变量$x$, 还车数为随机变量$y$，收益为$r$，则有：
    p ( x ∣ s ) = λ x x ! e − λ p(x|s) = \frac{\lambda^x}{x!}e^{-\lambda} p(x∣s)=x!λx​e−λ
    p ( y ∣ s ) = λ y y ! e − λ p(y|s) = \frac{\lambda^y}{y!}e^{-\lambda} p(y∣s)=y!λy​e−λ
    s ′ = s + y − x s' = s + y - x s′=s+y−x
    r ( s ) = 10 ∗ ∑ x p ( x ) ∗ min ⁡ ( x , s ) r(s) = 10 * \sum_{x} p(x)*\min(x, s) r(s)=10∗x∑​p(x)∗min(x,s) 这里是因为如果租车数大于车辆数，那么只能租出车辆数目的车辆。

    • 状态转移概率 p ( s ′ , r ∣ s ) p(s',r|s) p(s′,r∣s)为：
      p ( s ′ , r ∣ s ) = p ( s ′ ∣ s ) ∗ p ( r ∣ s ) = p ( s ′ ∣ s ) = ∑ x , y p ( x , y ∣ s ) = ∑ x , y p ( x ∣ s ) ∗ p ( y ∣ s ) s.t.  s ′ = s + y − x p(s',r|s) = p(s'|s)*p(r|s) = p(s'|s) = { \sum_{x,y} p(x,y|s) } = \sum_{x,y} p(x|s)*p(y|s) \\ \text{s.t. } s' = s + y - x p(s′,r∣s)=p(s′∣s)∗p(r∣s)=p(s′∣s)=x,y∑​p(x,y∣s)=x,y∑​p(x∣s)∗p(y∣s)s.t. s′=s+y−x

  • 值函数$V(s)$为：
    V ( s ) = ∑ s ′ , r p ( s ′ , r ∣ s ) ∗ [ r + γ ∗ V ( s ′ ) ] V(s) = \sum_{s',r} p(s',r|s) * [r + \gamma * V(s')] V(s)=s′,r∑​p(s′,r∣s)∗[r+γ∗V(s′)]

    • 这里的$\gamma$是折扣因子，取0.9。

  • 策略$\pi (s)$为：
    π ( s ) = arg ⁡ max ⁡ a ∑ s ′ , r p ( s ′ , r ∣ s , a ) ∗ [ r + γ ∗ V ( s ′ ) ] \pi(s) = \arg\max_{a} \sum_{s',r} p(s',r|s,a) * [r + \gamma * V(s')] π(s)=argamax​s′,r∑​p(s′,r∣s,a)∗[r+γ∗V(s′)]

• 算法实现：
  由上面的分析，我们可以得到状态转移概率 p ( s ′ , r ∣ s ) p(s',r|s) p(s′,r∣s)，值函数$V(s)$，策略$\pi (s)$。我们可以用动态规划的方法求解值函数$V(s)$，然后根据值函数求解策略$\pi (s)$。我们可以使用上面讲的策略迭代法或者值迭代法来求解。下面给出两种方法的python代码：

  import numpy as np
  import matplotlib.pyplot as plt
  from mpl_toolkits.mplot3d import axes3d
  import seaborn as sns; sns.set()MAX_CAR_GARAGE = 20 # 最多可容纳的汽车数
  MAX_CAR_MOVE = 5 # 最多可移动的汽车数
  lambda_rent = [3,4] # 租车点的租车率
  lambda_ret = [3,2] # 租车点的还车率
  accurate = 1e-6 # 精度限制
  rent_income = 10 # 租车收益
  move_cost = 2 # 移动汽车的成本
  discount = 0.9 # 折扣因子# 泊松分布概率密度函数
  def possion_prob(lam, n):return np.exp(-lam) * (lam**n) / np.math.factorial(n)# 租车场地类
  class RentCarPlace:def __init__(self, name, lam_rent, lam_ret, state:np.array, action:np.array):self.name = name # 场地名称self.lam_rent = lam_rent # 租车率self.lam_ret = lam_ret # 还车率self.state = state # 场地状态, 也就是汽车数self.action = action # 场地动作self.rewards = np.zeros(self.state.shape) # 奖励self.trans_probs = np.zeros((self.state.shape[0], self.state.shape[0])) # 转移概率# 解决方案类
  class Solution:def __init__(self, places:list[RentCarPlace]):self.places = placesself.value = np.zeros((places[0].state.shape[0], places[1].state.shape[0]))self.policy = np.zeros((places[0].state.shape[0], places[1].state.shape[0]))self.policy_stable = False# 收敛精度self.delta = 0.1self.cal_prob_reward()# 计算概率，p(s',r|s)和收益R(s)def cal_prob_reward(self):for i in range(len(self.places)):for s in self.places[i].state:x = 0while True:px = possion_prob(self.places[i].lam_rent, x)if px < accurate:breakz = min(x, s)self.places[i].rewards[s] += px * rent_income * zy = 0while True:py = possion_prob(self.places[i].lam_ret, y)if py < accurate:breaks_next = min(s - z + y, MAX_CAR_GARAGE)self.places[i].trans_probs[s, s_next] += px * pyy += 1x += 1# 策略评估，计算状态价值函数V(s)，使用迭代法，直到收敛，即V(s)变化小于精度限制，v(s) = sum(p(s',r|s) * (r + discount * v(s')))   def policy_evaluation(self):while True:delta = 0for s_a in self.places[0].state:for s_b in self.places[1].state:v = self.value[s_a, s_b]a = self.policy[s_a, s_b]self.value[s_a, s_b] = self.cal_value(s_a, s_b, a)delta = max(delta, abs(v - self.value[s_a, s_b]))if delta < self.delta:break# 策略改进，计算最优策略，即最优动作，使用贪心法，即a* = argmax_a(sum(p(s',r|s) * (r + discount * v(s'))))def policy_improvement(self):self.policy_stable = Truefor s_a in self.places[0].state:for s_b in self.places[1].state:old_action = self.policy[s_a, s_b]max_value = 0max_action = 0for a in range(-MAX_CAR_MOVE, MAX_CAR_MOVE+1):if a > s_a or a < 0 and abs(a) > s_b:continuevalue = self.cal_value(s_a, s_b, a)if value > max_value + self.delta:max_value = valuemax_action = aself.policy[s_a, s_b] = max_actionif old_action != max_action:self.policy_stable = False# 策略迭代，先评估，再改进，直到策略不再变化def policy_iteration(self):i = 0while not self.policy_stable:i += 1print('第{}次迭代'.format(i))self.policy_evaluation()self.policy_improvement()# self.save(i)# 价值迭代，先改进，再评估，直到价值函数不再变化def value_iteration(self):i = 0while True:i += 1print('第{}次迭代'.format(i))delta = 0for s_a in self.places[0].state:for s_b in self.places[1].state:old_value = self.value[s_a, s_b]max_value = 0max_action = 0for a in range(-MAX_CAR_MOVE, MAX_CAR_MOVE+1):if a > s_a or a < 0 and abs(a) > s_b:continuevalue = self.cal_value(s_a, s_b, a)if value > max_value + self.delta:max_value = valuemax_action = aself.value[s_a, s_b] = max_valueself.policy[s_a, s_b] = max_actiondelta = max(delta, abs(old_value - self.value[s_a, s_b]))if delta < self.delta:break# 计算价值函数def cal_value(self, s_a, s_b, a):if a > s_a: # A地点移动汽车数大于A地点汽车数a = s_aelif a < 0 and abs(a) > s_b: # B地点移动汽车数大于B地点汽车数a = -s_bs_a_next = int(min(s_a - a, MAX_CAR_GARAGE))s_b_next = int(min(s_b + a, MAX_CAR_GARAGE))  # 从(s_a, s_b)到(s_a_next, s_b_next)cost = -abs(a) * move_costfor s_a in self.places[0].state:for s_b in self.places[1].state:cost += self.places[0].trans_probs[s_a_next, s_a] * self.places[1].trans_probs[s_b_next, s_b] * (self.places[0].rewards[s_a_next] + self.places[1].rewards[s_b_next] + discount * self.value[s_a, s_b])return cost#保存最优策略和价值函数def save(self, i):np.save('policy_{}.npy'.format(i), self.policy)np.save('value_{}.npy'.format(i), self.value)# 加载最优策略和价值函数def load(self, i):self.policy = np.load('policy_{}.npy'.format(i))self.value = np.load('value_{}.npy'.format(i))def plot_policy(self, title=None):plt.rc('font',family='Times New Roman',size='10')   # 设置字体样式、大小policy = self.policy.astype(np.int32)fig, ax = plt.subplots()im = ax.imshow(policy, origin='lower', cmap='Blues')ax.figure.colorbar(im, ax=ax) # 侧边的颜色条带plt.grid(False)ax.set(xticks=np.arange(policy.shape[1]),yticks=np.arange(policy.shape[0]),title=title,ylabel='state of A',xlabel='state of B')for i in range(policy.shape[0]):for j in range(policy.shape[1]):ax.text(j, i, str(int(policy[i, j])), ha="center", va="center", color='#f05b72', fontsize=10)fig.savefig('policy.png', dpi=300)def plot_value(self, title=None):plt.rc('font',family='Times New Roman',size='10')   # 设置字体样式、大小fig, ax = plt.subplots(subplot_kw={"projection": "3d"})# 画mesh图x = np.arange(0, MAX_CAR_GARAGE+1)y = np.arange(0, MAX_CAR_GARAGE+1)X, Y = np.meshgrid(x, y)Z = self.valueax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')ax.set_title(title)ax.set_xlabel('state of A')ax.set_ylabel('state of B')ax.set_zlabel('value')fig.savefig('value.png', dpi=300)if __name__ == '__main__':# 1. 初始化两个租车点rent_car_place = [RentCarPlace('A', lambda_rent[0], lambda_ret[0], np.arange(0, MAX_CAR_GARAGE+1), np.arange(-MAX_CAR_MOVE, MAX_CAR_MOVE+1)),RentCarPlace('B', lambda_rent[1], lambda_ret[1], np.arange(0, MAX_CAR_GARAGE+1), np.arange(-MAX_CAR_MOVE, MAX_CAR_MOVE+1))]# 2. 初始化解决方案solution = Solution(rent_car_place)# 3. 策略迭代solution.policy_iteration()# 4. 价值迭代# solution.value_iteration()# 5. 画出最优策略和价值函数solution.plot_policy("Optimal Policy")solution.plot_value("Optimal Value")plt.show()# 6. 加载最优策略和价值函数# solution.load(5)# solution.plot_policy()
  

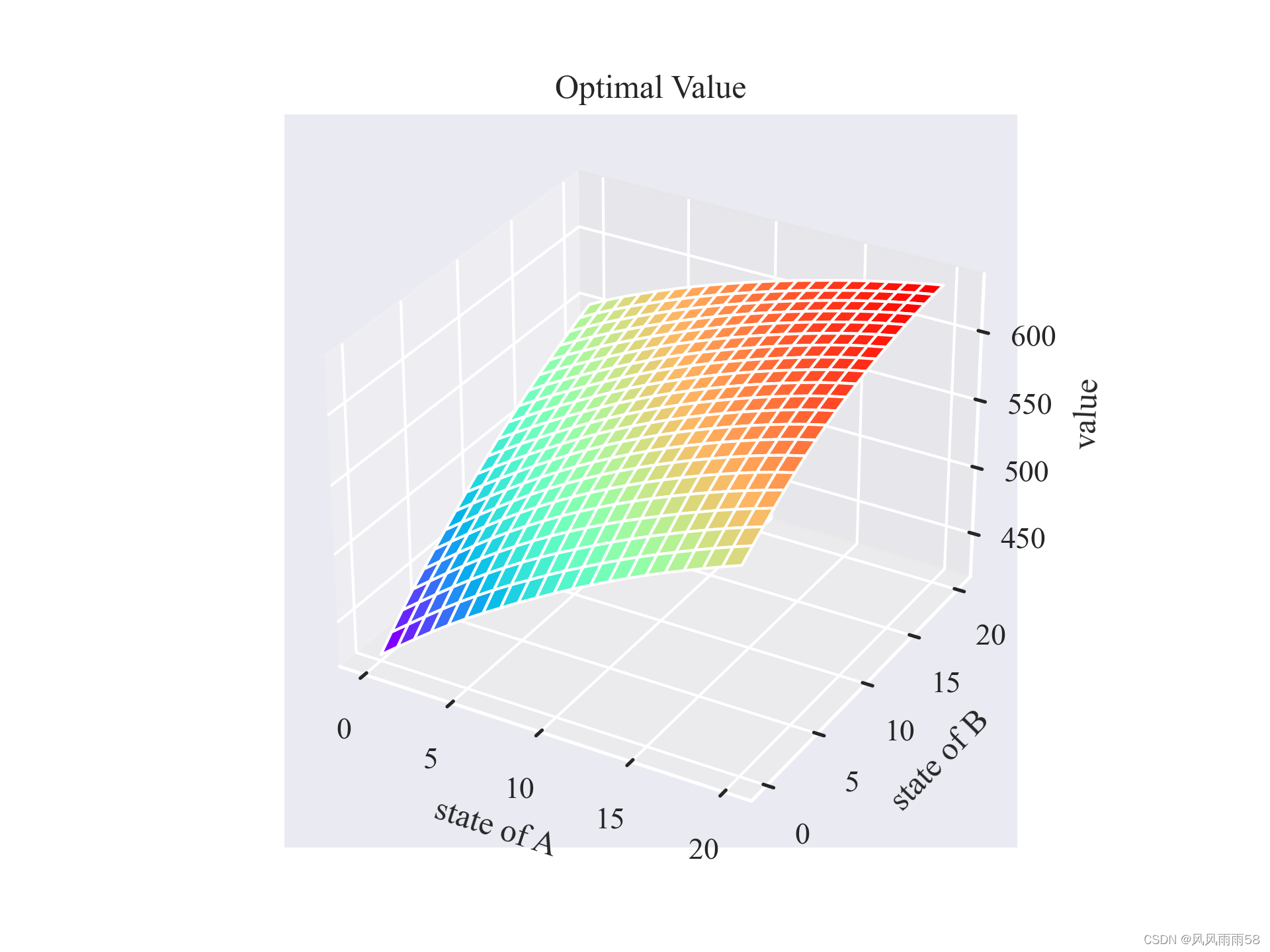
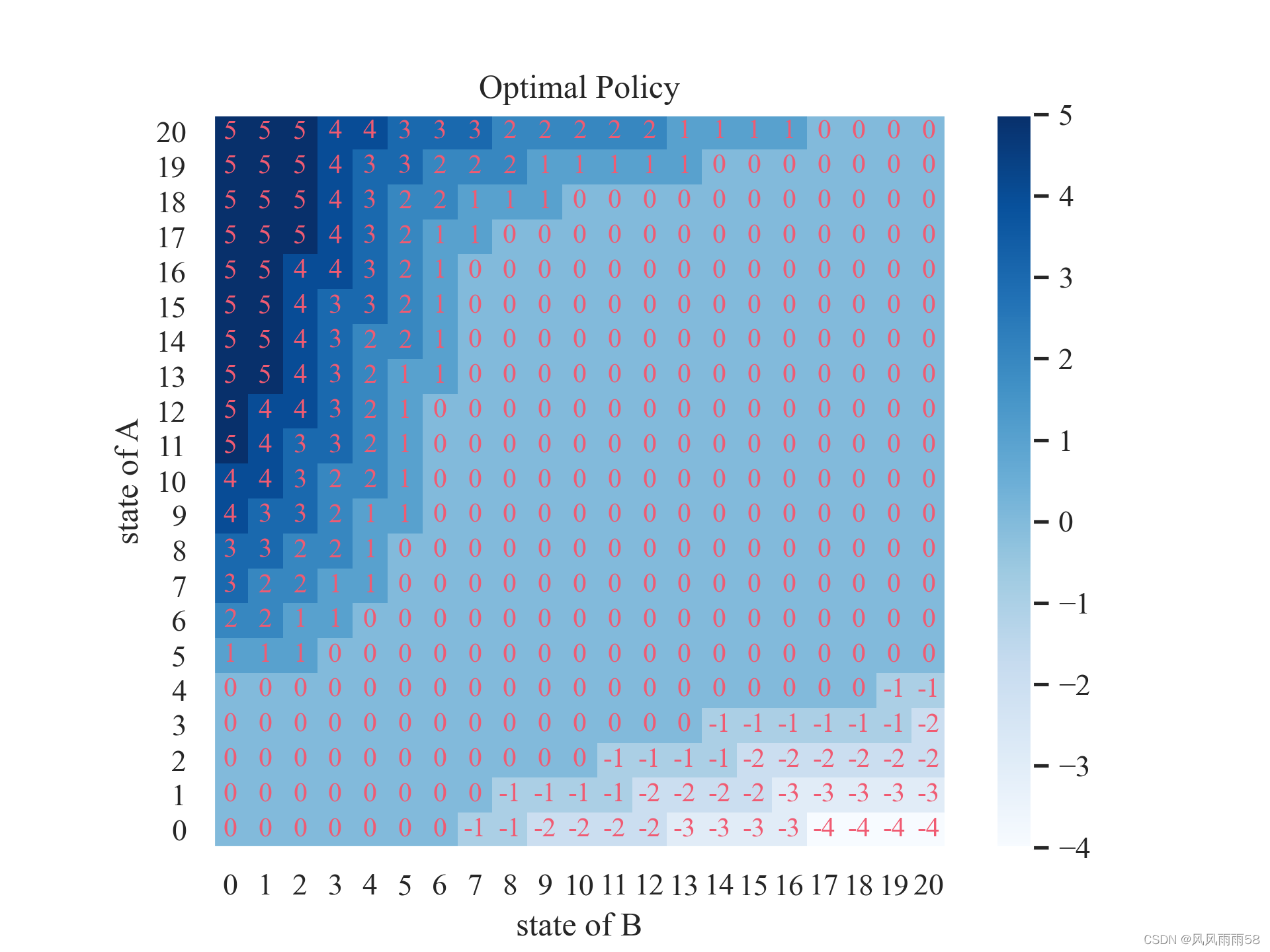
  • 运行结果
    
    

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！