油克小学期（五）局部最优搜索（2）多元函数极值求解

局部最优搜索过程流程图：

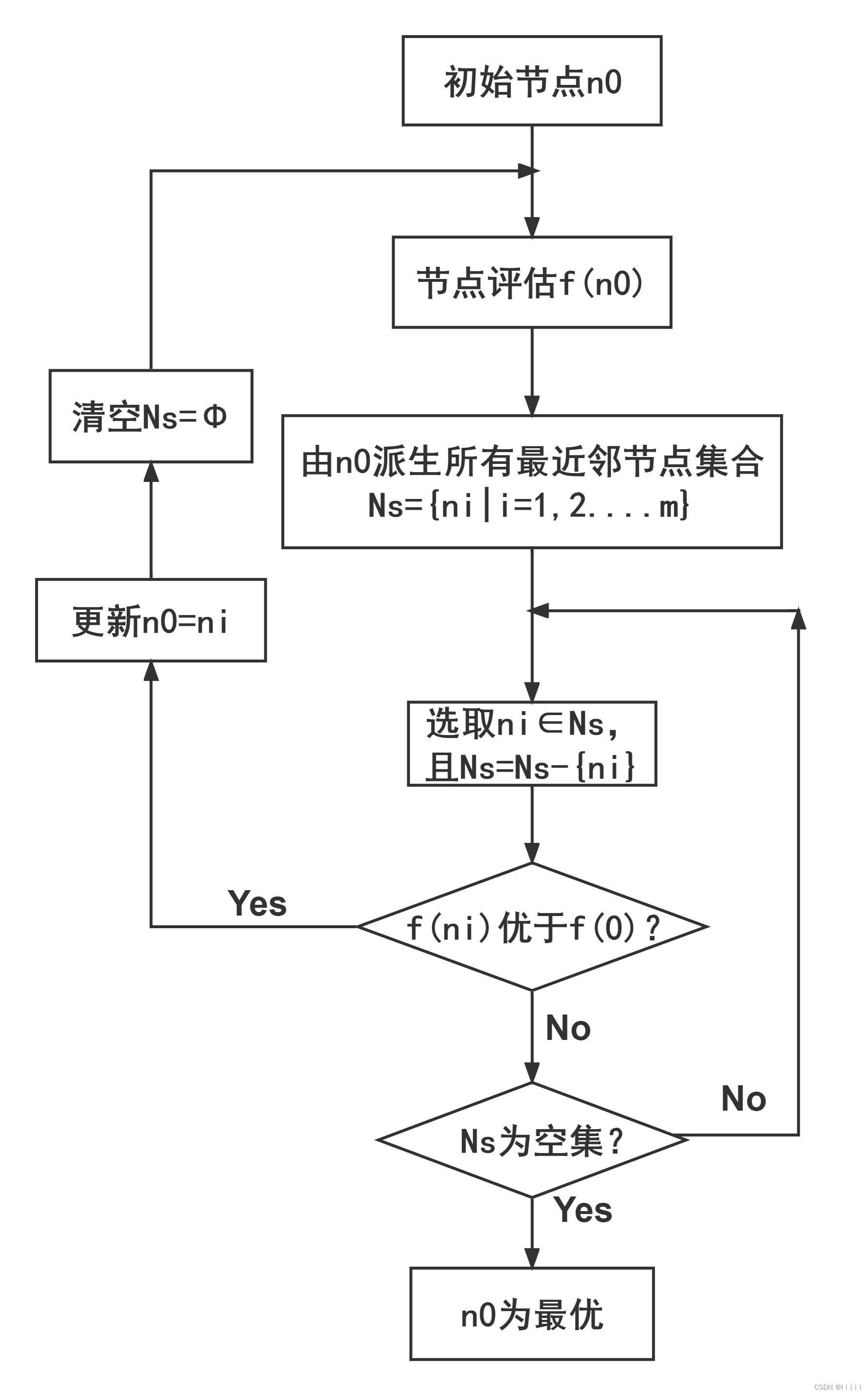
局部优先算法归纳：

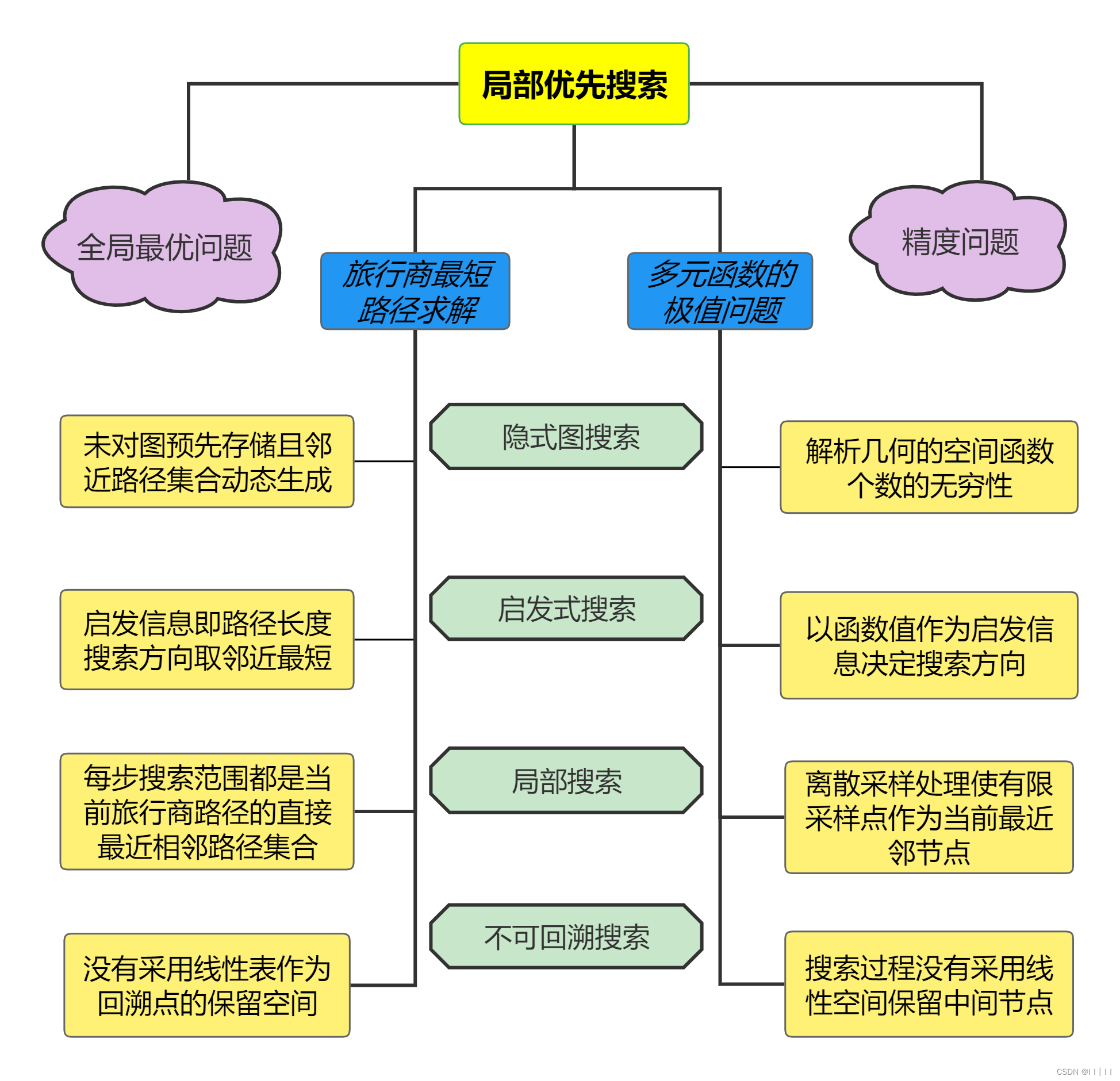
代码实现：

```c
#include 
#include 
#include 
#include 
#include #define LEFT -5 //区间左边界
#define RIGHT 5 //区间右边界
#define TRUE 1 //符号常量, 真
#define FALSE 0 //符号常量, 假
#define NEIGHBORNUM 8 //最近邻 8 个节点
typedef int STATUS; //真假逻辑类型
typedef struct //三维数据表示, 存储空间节点
{double x1, x2, y; //三维空间坐标
} POINT; //三维空间坐标类型(搜索空间节点类型)double fun(double x1, double x2) { //待求解的函数double y;y = 3 * (1 - x1) * (1 - x1) * exp(-(x1 * x1) - (x2 + 1) * (x2 + 1))- 10 * (x1 / 5 - x1 * x1 * x1 - x2 * x2 * x2 * x2 * x2) * exp(-x1 * x1 - x2 * x2)- exp(-(x1 + 1) * (x1 + 1) - x2 * x2) / 3;return y;
}POINT *Expand(POINT point, double delta,double (*fun)()) { //给定当前节点的派生邻近节点int i = 0;double x1, x2;POINT *neighbors; //最近邻节点的存储单元neighbors = (POINT *) malloc(sizeof(POINT) * NEIGHBORNUM);for (x1 = point.x1 - delta; x1 <= point.x1 + delta; x1 += delta) //当前节点的 8 个方向for (x2 = point.x2 - delta; x2 <= point.x2 + delta; x2 += delta) //固定步长 delta{ //当前节点不作为派生邻近节点if (fabs(point.x1 - x1) < 1e-10 && fabs(point.x2 - x2) < 1e-10) continue;neighbors[i].x1 = x1 < LEFT ? LEFT : (x1 > RIGHT ? RIGHT : x1); // 节点在区间内neighbors[i].x2 = x2 < LEFT ? LEFT : (x2 > RIGHT ? RIGHT : x2);neighbors[i].y = fun(x1, x2); //区间内的函数值i++;}return neighbors; //所有派生邻近节点
}void ClearAllNeighbors(POINT *neighbors) { // 动态开辟存储空间并回收free(neighbors);
}void InitPoint(POINT *point) { // 随机给定初始节点极其函数值srand((unsigned) time(NULL)); //当前计算机时间为随机数种子point->x1 = rand() % (int) (RIGHT - LEFT) + LEFT; //随机数在区间[LEFT, RIGHT]内point->x2 = rand() % (int) (RIGHT - LEFT) + LEFT; //随机数在区间[LEFT, RIGHT]内point->y = fun(point->x1, point->x2);//函数值
}void SearchResult_by_Mini(double delta, double (*fun)(),POINT *result) {                                                           // 根据搜索步长delta求解函数fun, 求解局部最优结果resultSTATUS flag = TRUE; //默认当前最小POINT point, *neighbors; //当前节点, 派生最近邻节点集合int i;InitPoint(&point); //随机初始化起始节点printf("Init Fum(%lf, %lf)=%lf\n", point.x1, point.x2, point.y);// 显示初始节点的坐标值while (TRUE) //无线搜索求解{neighbors = Expand(point, delta, fun); //所有邻近节点for (i = 0; i < NEIGHBORNUM; i++) //逐一比较判断if (point.y < neighbors[i].y) //当前函数值小于邻近节点的值{ //当前函数值小于某个邻近节点的值flag = TRUE; //找到更小的邻近节点的值point = neighbors[i]; //更新当前节点break; //不再比较其他邻近节点的值}if (flag == TRUE) //邻近节点的值更小, 需继续查找flag = FALSE; //再次查找当前节点else //当前函数值最小break; //无须再求解ClearAllNeighbors(neighbors); //清除所有邻近节点}*result = point; //当前节点的值为最优结果
}void main() {POINT result;double delta = 0.0001;int i, j, k;for (i = 0; i < 5; i++) {SearchResult_by_Mini(delta, fun, &result);printf("Resu Fun(%lf, %lf)=%lf\n", result.x1, result.x2, result.y);printf("==========================\n");for (j = 0; j < 32767; j++)for (k = 0; k < 32767; k++);// 延时, 产生不同随机数种子}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！