文章目录

• 1. 三者的关系
• 2. 熵
• 3. 交叉熵
• 4. KL散度

1. 三者的关系

1. KL散度=交叉熵-熵
2. 熵：可以表示一个事件A的自信息量，也就是A包含多少信息。
3. KL散度：可以用来表示从事件A的角度来看，事件B有多大不同，适用于衡量事件A，B之间的差异。
4. 交叉滴：可以用来表示从事件A的角度来看，如何描述事件B，适用于衡量不同事件B之间的差异；
5. 对于不同的事件B，计算事件AB的KL散度时都同时减去事件A的熵（KL散度=交叉熵-熵（A）），因此，如果只是比较不同B事件之间的差异，计算交叉熵和计算KL散度是等价的。
6. 交叉熵、KL散度都不具备对称性

总结：KL散度可以被用于计算代价，而KL散度=交叉熵-熵，在特定情况下最小化KL散度等价于最小化交叉熵。交叉熵的运算更简单，所以用交叉熵来当做代价。

2. 熵

熵的公式如下：

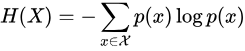
其中p(x)表示x事件发生的概率

3. 交叉熵

从公式上来看，求A和B的交叉熵就是把事件A求熵公式中的部分统计量换成B的统计量，如果对A自己求交叉熵等价于求熵
 在多分类问题中，损失函数（loss function）为交叉熵（cross entropy）损失函数。对于样本点(x,y)来说，y是真实的标签，在多分类问题中，其取值只可能为标签集合labels. 我们假设有K个标签值，且第i个样本预测为第k个标签值的概率为pi,k， 即：
p i , k = Pr ⁡ ( t i , k = 1 ) p_{i,k} = \operatorname{Pr}(t_{i,k} = 1) pi,k​=Pr(ti,k​=1)
一共有N个样本，则该数据集的损失函数为

L log ⁡ ( Y , P ) = − log ⁡ Pr ⁡ ( Y ∣ P ) = − 1 N ∑ i = 0 N − 1 ∑ k = 0 K − 1 y i , k log ⁡ p i , k L_{\log}(Y, P) = -\log \operatorname{Pr}(Y|P) = - \frac{1}{N} \sum_{i=0}^{N-1} \sum_{k=0}^{K-1} y_{i,k} \log p_{i,k} Llog​(Y,P)=−logPr(Y∣P)=−N1​i=0∑N−1​k=0∑K−1​yi,k​logpi,k​

• 最内层是第i个样本被分到第k类别的真实概率 * log（第i个样本被分到第k类别的预测概率）
• 外层首先对所有同一样本的所有类别求和，然后对所有样本求和，最后除以样本数量

4. KL散度

KL散度公式如下：
D ( p ∣ ∣ q ) = ∑ x p ( x ) log ⁡ p ( x ) − ∑ x p ( x ) log ⁡ q ( x ) D(p||q)=\sum_{x}p(x) \log p(x) - \sum_{x}p(x) \log q(x) D(p∣∣q)=x∑​p(x)logp(x)−x∑​p(x)logq(x)
等价于：

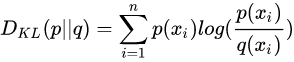
通过上述公式可知：KL散度=交叉熵-熵，KL散度在p(x)和q(x)相同时取到最小值0，两个概率分布越相似，则KL散度越小。
KL散度包含如下性质；

1. 不对称性，即：
   D K L ( P ∣ ∣ Q ) ≠ D K L ( Q ∣ ∣ P ) D_{KL}(P||Q) \neq D_{KL}(Q||P) DKL​(P∣∣Q)​=DKL​(Q∣∣P)
2. 非负性，即：
   D K L ( P ∣ ∣ Q ) ≥ 0 D_{KL}(P||Q) \geq 0 DKL​(P∣∣Q)≥0

参考文章->

1. 交叉熵与KL散度
2. 交叉熵、相对熵（KL散度）、JS散度和Wasserstein距离（推土机距离）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！