主成分分析—PCA

笔记

一、定义

主成分分析（Principal Components Analysis ，PCA)也称为主分量分析，是一种通过降维来简化数据结构的方法，即把原有的多个指标转化成少数几个代表性较好的综合指标，这少数几个指标能够反映原来指标的大部分信息（80%以上），并且各个指标之间保持独立，避免出现重叠信息。

注意：进行主成分的变量之间必须要有相关性，经过分析后变量之间独立
主成分：在力求数据信息丢失最少的原则下，对高维的变量空间降维，即研究指标体系的少数几个线性组合，并且这几个线性组合所构成的综合指标将尽可能多地保留原来指标变异方面的信息。这些综合指标就称为主成分。

二、主成分分析法基本原理

1. 主成分分析就是设法将原来众多具有一定相关性的变量(如p个变量)，重新组合成一组新的相互无关的综合变量来代替原来变量。
2. 通常数学上的处理就是将原来p个变量作线性组合作为新的综合变量。
3. 如果将选取的第一个线性组合即第一个综合变量记为F1，自然希望F1尽可能多的反映原来变量的信息。

若var(F1)越大，表示F1包含的信息越多。因此在所有的线性组合中所选取的F1应该是方差最大的，故称之为第一主成分（principal component I）。
如果第一主成分不足以代表原来p个变量的信息，再考虑选取F2即第二个线性组合。F2称为第二主成分（principal component II）

三、数学模型

假设我们所讨论的实际问题中，有 p 个指标，我们把这p个指标看作 p 个随机变量，记为 X 1 X_1 X1​， X 2 X_2 X2​，…， X p X_p Xp​，主成分分析就是要把这 p 个指标的问题，转变为讨论 m 个新的指标 F 1 F_1 F1​， F 2 F_2 F2​，…， F k F_k Fk​(k<=p），按照保留主要信息量的原则充分反映原指标的信息，并且相互独立。

这种由讨论多个指标降为少数几个综合指标的过程在数学上就叫做降维。主成分分析通常的做法是，寻求原指标的线性组合 F i F_i Fi​

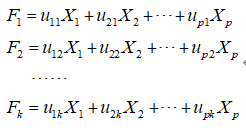
满足如下的条件：

1. 每个主成分的系数平方和为1。即
   
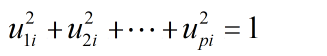
2. 主成分之间相互独立，即无重叠的信息。即
   
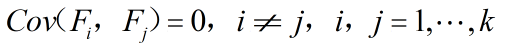
   3.主成分的方差依次递减，重要性依次递减，即
   

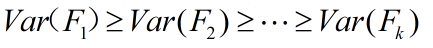
四、主成分分析的几何解释

如果我们将x刘轴和×2轴先平移，再同时按逆时针方向旋转0角度，得到新坐标轴FI和F2。
FI和F2是两个新变量。

旋转变换的目的是为了使得n个样品点在 F l F_l Fl​轴方向上的离散程度最大，即 F l F_l Fl​的方差最大。变量 F l F_l Fl​代表了原始数据的绝大 部分信息，在研究某经济问题时，即使不考虑变量 F 2 F_2 F2​也无损大局。经过上述旋转变换原始数据的大部分信息集中到 F l F_l Fl​轴上，对数据中包含的信息起到了浓缩作用。

F l F_l Fl​， F 2 F_2 F2​除了可以对包含在 X l X_l Xl​， X 2 X_2 X2​中的信息起着浓缩作用之外，还具有不相关的性质，这就使得在研究复杂的问题时避免了信息重叠所带来的虚假性。二维平面上的n个点的方差大部分都归结在 F l F_l Fl​轴上，而 F 2 F_2 F2​轴上的方差很小。 F l F_l Fl​和 F 2 F_2 F2​称为原始变量 x 1 x_1 x1​和 x 2 x_2 x2​的综合变量。F简化了系统结构，抓住了主要矛盾。

五、主成分的推导及性质

1.两个线性代数的结论

（1）若A是p阶实对称阵，则一定可以找到正交阵U，使得

其中 λ i λ_i λi​，i=1.2.…p 是A的特征根。

（2）若上述矩阵的特征根所对应的单位特征向量为 u 1 u_1 u1​,…, u p u_p up​

令

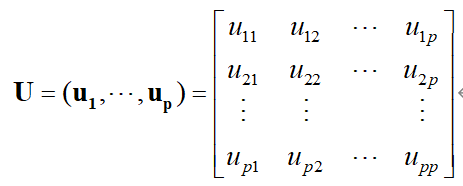
则实对称阵A属于不同特征根所对应的特征向量是正交的，即有U’U=UU’=I

2.主成分的推导

（一）第一主成分

设X
设X的协方差阵为

由于 Σ x Σ_x Σx​为非负定的对称阵，则利用线性代数的知识可得，必存在正交阵U，使得

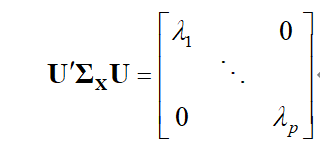
其中 λ 1 λ_1 λ1​， λ 2 λ_2 λ2​，…， λ p λ_p λp​为 Σ x Σ_x Σx​的特征根，不妨假设 λ 1 λ_1 λ1​>= λ 2 λ_2 λ2​>=…>= λ p λ_p λp​。而U恰好是由特征根相对应的特征向量所组成的正交阵。


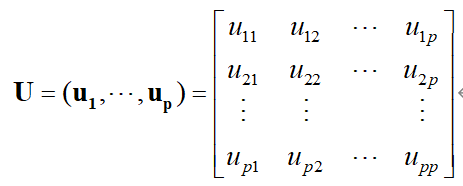
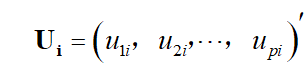
设有P维正交向量

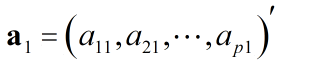
通过线性组合，构造一个新的变量 F 1 F_1 F1​

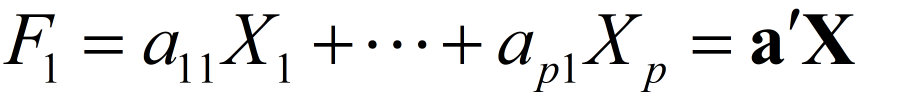
因此 F 1 F_1 F1​的方差为：




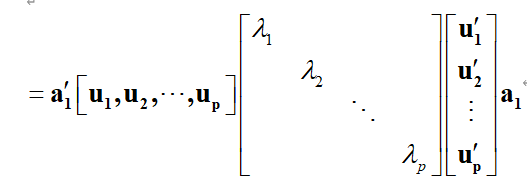
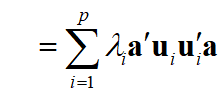
当且仅当 a 1 a_1 a1​= u 1 u_1 u1​时，即员 F 1 F_1 F1​= u 11 u_{11} u11​ X 1 X_1 X1​+…+ u p 1 u_{p1} up1​ X p X_p Xp​时，有最大的方差 λ 1 λ_1 λ1​。因为Var( F 1 F_1 F1​)= λ 1 λ_1 λ1​。
如果第一主成分的信息不够，则需要寻找第二主成分。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！