湖湘杯 2021 Crypto (连分数运用)

湖湘杯 2021 Crypto

• • 1.题目
  • 2.分析
  • 3.实现
  • • sage计算连分数精度不够的原因...

连分数 continued_fraction

比赛当时这道题被A爆了，但我就是做不出来。心态炸了。

前几天打西湖，学了点Wiener Attack和连分数，又打开了一直存在桌面的这道题，豁然开朗。

1.题目

from Crypto.Util.number import *
import random
from math import *
from gmpy2 import *
'''
m1 = bytes_to_long(flag[:len(flag) // 2])
m2 = bytes_to_long(flag[len(flag) // 2:])
'''
def gen(pbits, qbits):p1, q1 = getPrime(pbits), getPrime(qbits)n1 = p1**4*q1q2 = getPrime(qbits)bound = p1 // (8*q1*q2) + 1#360-3-q-q=101p2 = random.randrange(p1, p1 + bound)while not isPrime(p2):p2 = random.randrange(p1, p1 + bound)n2 = p2**4*q2return (n1, n2), (p1, q1), (p2, q2)e = 0x10001
pbits = int(360)
qbits = int(128)
'''
pk, sk1, sk2 = gen(pbits, qbits)
c1 = pow(m1, e, pk[0])
c2 = pow(m2, e, pk[1])
print(f'pk = {pk}')
print(f'c1, c2 = {c1, c2}')
'''pk = (1150398070565459492080597718626032792435556703413923483458704675295997646493249759818468321328556510074044954676615760446708253531839417036997811506222349194302791943489195718713797322878586379546657275419261647635859989280700191441312691274285176619391539387875252135478424580680264554294179123254566796890998243909286508189826458854346825493157697201495100628216832191035903848391447704849808577310612723700318670466035077202673373956324725108350230357879374234418393233, 1242678737076048096780023147702514112272319497423818488193557934695583793070332178723043194823444815153743889740338870676093799728875725651036060313223096288606947708155579060628807516053981975820338028456770109640111153719903207363617099371353910243497871090334898522942934052035102902892149792570965804205461900841595290667647854346905445201396273291648968142608158533514391348407631818144116768794595226974831093526512117505486679153727123796834305088741279455621586989)
n1,n2 = pk
c1, c2 = (361624030197288323178211941746074961985876772079713896964822566468795093475887773853629454653096485450671233584616088768705417987527877166166213574572987732852155320225332020636386698169212072312758052524652761304795529199864805108000796457423822443871436659548626629448170698048984709740274043050729249408577243328282313593461300703078854044587993248807613713896590402657788194264718603549894361488507629356532718775278399264279359256975688280723740017979438505001819438, 33322989148902718763644384246610630825314206644879155585369541624158380990667828419255828083639294898100922608833810585530801931417726134558845725168047585271855248605561256531342703212030641555260907310067120102069499927711242804407691706542428236208695153618955781372741765233319988193384708525251620506966304554054884590718068210659709406626033891748214407992041364462525367373648910810036622684929049996166651416565651803952838857960054689875755131784246099270581394)
from Crypto.Util.number import *

2.分析

给了 n 1 , n 2 n_1,n_2 n1​,n2​,需要进行分解。首先gcd试一下，是1，无果。

p 1 , p 2 p_1,p_2 p1​,p2​之间有一个bound的约束

bound = p1 // (8*q1*q2) + 1

bound的大小大概是101位数，相对于p的360位是很小的。

题目给的关系
n 1 = p 1 4 ∗ q 1 n_1=p_1^4*q1 n1​=p14​∗q1
n 2 = p 2 4 ∗ q 2 n_2=p_2^4*q2 n2​=p24​∗q2
并且知道 p 1 , p 2 p_1,p_2 p1​,p2​ 差距很小，但 q 1 和 q 2 q_1和q_2 q1​和q2​的大小并不知道

n 1 n 2 = ( p 1 p 2 ) 4 ∗ q 1 q 2 \frac{n_1}{n_2}=(\frac{p_1}{p_2})^4*\frac{q_1}{q_2} n2​n1​​=(p2​p1​​)4∗q2​q1​​

p 1 p 2 \frac{p_1}{p_2} p2​p1​​的大小之前提到，很接近1，并且小于1

所以就能得知 q 1 q 2 \frac{q_1}{q_2} q2​q1​​的大小和 n 1 n 2 \frac{n_1}{n_2} n2​n1​​十分接近，并且

n 1 n 2 < q 1 q 2 \frac{n_1}{n_2}\lt\frac{q_1}{q_2} n2​n1​​<q2​q1​​

我们通过连分数构造出 n 1 n 2 \frac{n_1}{n_2} n2​n1​​的连分数数列

如果某个分数的分子和分母（这里就代表 q 1 q_1 q1​和 q 2 q_2 q2​）刚好能被 n 1 n_1 n1​和 n 2 n_2 n2​整除，则就成功分解，分子和分母也就是我们要找的 q 1 q_1 q1​和 q 2 q_2 q2​，进而求出 p 1 p_1 p1​和 p 2 p_2 p2​

3.实现

sage内实现连分数

sage: c = continued_fraction(n1/n2)
sage: c
[0; 1, 12, 2, 6, 1, 11, 8, 1, 11, 1, 1, 3, 1, 2, 38]

发现精度并不够（破案了，精度够，是我搞错了，原因在最后）。应该是内置的浮点运算精度的原因，也就是传入的参数n1/n2精度太低
应该有改进的方法，但我还是手搓连分数吧，也好熟悉熟悉原理

看的徐师傅的代码

def contFrac(a,b):  # a/b 计算连分数数列cf = []while b:cf.append(a//b)a,b = b,a%breturn cf#连分数数列转换为分子和分母
def fun(cc):fz = 0 # numeratorfm = 1 # denominatorfor i in cc[::-1]:fz, fm = fm, fz + fm * ireturn fz,fm

第二个函数好像有点毛病，得把输出两个变量调换一下才行，虽然理论完全没错，数字也对的上，就是反过来了…

改为return fm,fz

开找

sage: cc = contFrac(n1,n2)
sage: for i in range(2,len(cc)):
....:     fz,fm = fun(cc[:i])  # 将数列的前i项传入函数
....:     if not (n1 % fz or n2 % fm): # 结果分别整除2个数
....:         print(i)
2
70

成功找到了!! i=70的时候
于是fz,fm = fun(cc[:70])

计算 p 1 , p 2 p_1,p_2 p1​,p2​

sage: fz,fm = frac2n(cc[:70])
sage: assert(n1%fz == 0 and n2 % fm == 0)
sage: q1,q2 = fz,fm
sage: p1_4,p2_4 = n1//q1,n2//q2
sage: from gmpy2 import iroot
sage: assert(all(iroot(i,4)[1] for i in [p1_4,p2_4]))
sage: p1,p2 = iroot(p1_4,4)[0], iroot(p2_4,4)[0]
sage: p1,p2
(mpz(1585915514180317814056421222155603344889755890858835238854910430992477836307761878218354454115222433205838763),
mpz(1585915514180317814056421222155603344889755890858835238854910430992477836307763352592140319849865816671914223))

这里的 n = p 4 ∗ q n=p^4*q n=p4∗q，
计算 φ ( n ) = ( q − 1 ) ∗ ( p 4 − p 3 ) \varphi(n)=(q-1)*(p^4-p^3) φ(n)=(q−1)∗(p4−p3)

sage: p1^4*q1==n1 and p2^4*q2 == n2
True
/*用命令行写脚本就是好随时验证*/
sage: phin1 = (q1-1)*(p1^4-p1^3)
sage: phin2 = (q2-1)*(p2^4-p2^3)
sage: e = 0x10001
sage: d1 = invert(e,phin1)
sage: d2 = invert(e,phin2)
sage: long_to_bytes(pow(c1,d1,n1))
b'flag{8ef333ac-21a7-11'
sage: long_to_bytes(pow(c2,d2,n2))
b'ec-80f1-00155d83f114}'

得到flag

flag{8ef333ac-21a7-11ec-80f1-00155d83f114}

我用交互命令行写的代码。没有完整脚本。

sage计算连分数精度不够的原因…

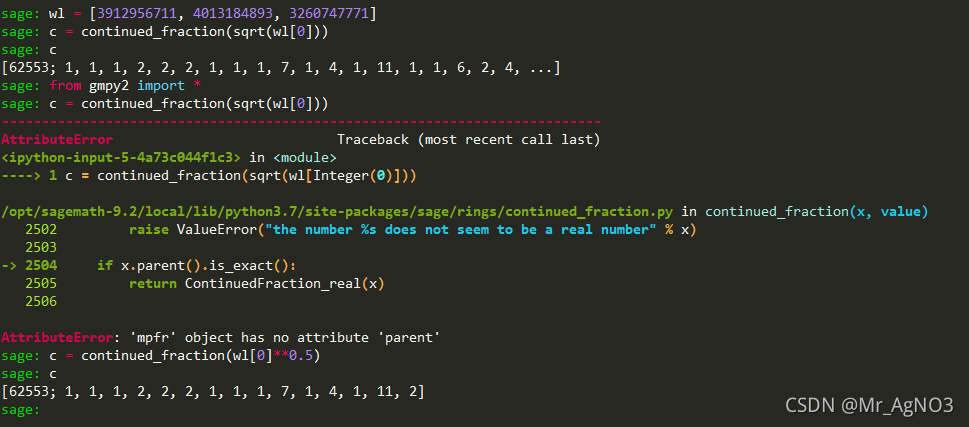
import gmpy2后，sqrt函数被重写了，数据类型不支持连分数函数continued_fraction
使用**0.5开方，导致精度不够.

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！