参数估计之区间估计（统计知识）以及Python代码

区间估计定义：

区间估计(interval estimate)
在点估计的基础上，根据样本统计量的抽样分布可以对样本统计量与总体样本的真实参数的接近程度求出一个概率度量，在此概率下给出总体参数估计的一个可信的区间范围。与区间估计常常一同出现的，还有置信区间的概念。
 

通俗解释：

对于区别点估计和区间估计，有个很通俗的解释：

我对待定参数只估计一个值（点估计），只笃定了这个值是最精确的；
我给出待定参数的一个估计范围（区间估计），猜测这个区间内至少有一个值使得待定参数最接近于真实值；
对于这个区间，给出一个概率（置信度）来说明这个区间内有多大的把握存在至少有一个值使得待定参数最接近于真实值；给出置信度的区间估计就是置信区间。
 

 置信区间的定义：

教材实例以及推理过程：

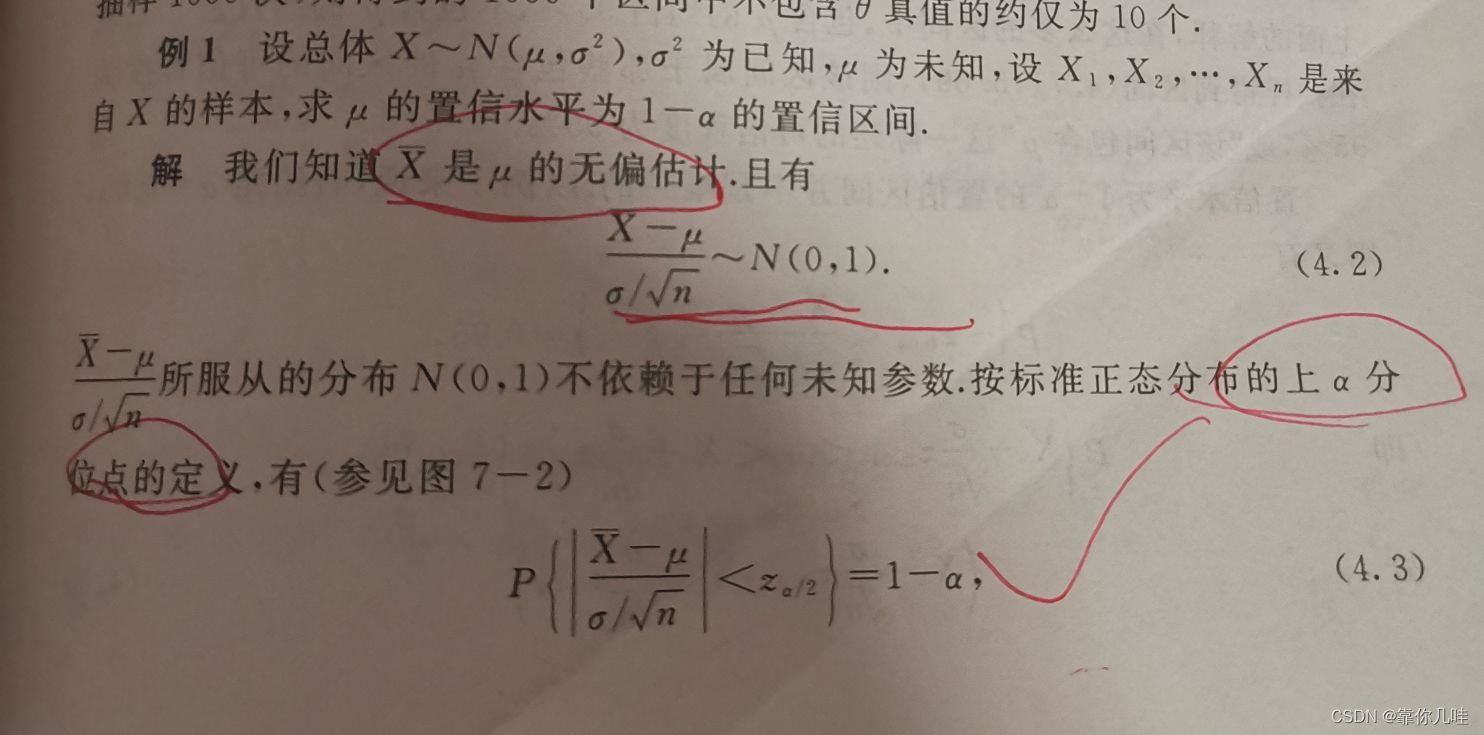
 图源于教材

Python代码部分（总体均值的置信区间估计）

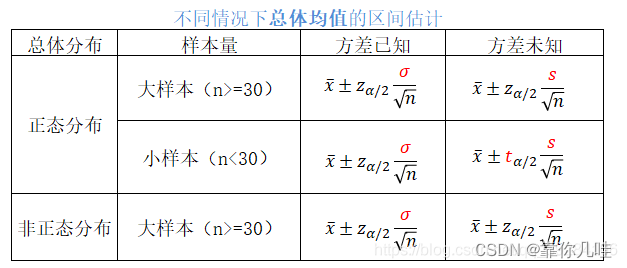
 1：统计学中以大于30的抽样容量为大样本

2：样本容量大于30，由中心极限定理可将均值看做符合正态分布

def mean_interval(mean=None, std=None, sig=None, n=None, confidence=0.95):"""mean:样本均值std：样本标准差sig: 总体方差n:   样本量confidence：置信水平功能：构建总体均值的置信区间"""alpha = 1 - confidencez_score = scipy.stats.norm.isf(alpha / 2)  # z分布临界值t_score = scipy.stats.t.isf(alpha / 2, df = (n-1) )  # t分布临界值if n >= 30 and sig != None:me = z_score*sig / np.sqrt(n)  # 误差lower_limit = mean - meupper_limit = mean + meif n >= 30 and sig == None:me = z_score*std / np.sqrt(n)lower_limit = mean - meupper_limit = mean + meif n < 30 and sig == None:me = t_score*std / np.sqrt(n)lower_limit = mean - meupper_limit = mean + mereturn (round(lower_limit, 3), round(upper_limit, 3))mean_interval(mean=8900, std=None, sig=500, n=35, confidence=0.95)
mean_interval(mean=8900, std=500, sig=None, n=35, confidence=0.90)
mean_interval(mean=8900, std=500, sig=None, n=35, confidence=0.99)

实例代码运算

 代码解答：

课本答案：

 代码解答:

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！