机器学习第四篇:SVM,SMO算法的实现
这两天摸索了SVM,刚开始的时候接触SMO的时候就很懵,但是我有机器学习三大法宝护体,最终还是搞懂了一些。
前面的细节部分就不予阐述了,直接从SMO算法部分开始讲起:
下面讨论具体方法:
(1)
(2)
(3)
(4)
(5)
(6)
利用上面这些等式来计算:
首先假设我们的初始可行解为,最优解为
,未经处理过的
的最优解为
,根据(5),
,y只有两种情况1和-1,然后在两种情况下我们来确定
的范围:
然后分情况讨论L,H的取值:
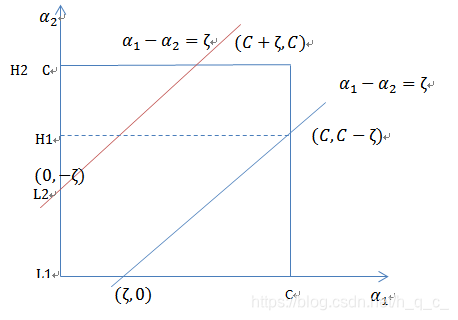
此时,则:
,
当时:
,
具体的详细的过程就不予阐述,可以参考李航的《统计学习方法》:
其中,所以
得到的,对其进行处理可以得到:
得到后,利用下面公式得到
:
现在我们可以进行对的更新了,那我们如何选择它呢:
第一个变量的选择:在代码当中用外层循环实现,外层循环中选取违反KKT条件最严重的样本点
第二个变量的选择:内层循环,假设已经找到了第一个变量,本意选择是希望能使第二个变量有足够大的变化,但在代码当中一般就选取最大的
更新了之后,我们也需要更新我们的b。
那么新的b应该选取谁比较合适呢?
如果在界内,那么就选
,如何
在界内,就选
,如果都在界内,那么
,如果都在界上,一般选取
在完成两个变量的优化之后,还必须更新我们的E
在编程之前再介绍一下SVM的损失函数:合页损失函数。
称为合页损失函数,下标+表示取正值的函数.
也就是说,当样本正确分类时,大于等于1的,损失为0,否则损失,
接下来就接受SMO算法的源代码:
先接受精简版的SMO:
输入我们的数据:
def loadDataSet(fileName):dataMat = []; labelMat = []#x存在datamat当中,y就是我们的标签,存在labelmat中fr = open(fileName)for line in fr.readlines():lineArr = line.strip().split('\t')dataMat.append([float(lineArr[0]), float(lineArr[1])])labelMat.append(float(lineArr[2]))#数据一共有三列,最后一列为yreturn dataMat,labelMat精简版就随机选择我们的alpha:
def selectJrand(i,m):j=i #we want to select any J not equal to iwhile (j==i):j = int(random.uniform(0,m))return j
提前定义一个的范围,以便后面使用:
def clipAlpha(aj,H,L):if aj > H: aj = Hif L > aj:aj = Lreturn aj然后就是我们的大餐了:
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()b = 0; m,n = shape(dataMatrix)#返回他的行列alphas = mat(zeros((m,1)))iter = 0 while (iter < maxIter):alphaPairsChanged = 0for i in range(m):fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b #这一步就是在计算我们的g(x),其中.T是np中的转置,可能并没有完全按照公式来,但只要能求得最后的结果你想怎么转就怎么转,注意矩阵下标,multiply是对位相乘,不是矩阵相乘运算。Ei = fXi - float(labelMat[i])if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):#就是检查误差E是否足够大,我们选择alpha的时候就是希望有很大的变化j = selectJrand(i,m)#随机挑选第二个alphafXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + bEj = fXj - float(labelMat[j])#计算出第二个EalphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();if (labelMat[i] != labelMat[j]):#按照前面的公式,确定L,HL = max(0, alphas[j] - alphas[i])H = min(C, C + alphas[j] - alphas[i])else:L = max(0, alphas[j] + alphas[i] - C)H = min(C, alphas[j] + alphas[i])if L==H: print ("L==H"); continueeta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T#这里是在计算eta,没有完全按照公式,把公式前面的正号变成负号就可以了if eta >= 0: print ("eta>=0"); continue#按照公式计算,eta>=0,但是没有按照公式计算就是eta<=0,所以出现eta>=0肯定错误alphas[j] -= labelMat[j]*(Ei - Ej)/eta#alpha2的更新公式alphas[j] = clipAlpha(alphas[j],H,L)if (abs(alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); continue#变化足够小,就不用变化了,迅速增加迭代次数,以退出程序alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
#update i by the same amount as jb1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].Tb2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].Tif (0 < alphas[i]) and (C > alphas[i]): b = b1elif (0 < alphas[j]) and (C > alphas[j]): b = b2else: b = (b1 + b2)/2.0#b的选择我在前面也有详细介绍alphaPairsChanged += 1print ("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))if (alphaPairsChanged == 0): iter += 1else: iter = 0print ("iteration number: %d" % iter)return b,alphas再附上完整的优化的SMO代码,其实变化不大,主要的变化在于E的更新与alpha的选择上面,上面懂了下面的也不会在话下:
class optStruct:def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters self.X = dataMatInself.labelMat = classLabelsself.C = Cself.tol = tolerself.m = shape(dataMatIn)[0]self.alphas = mat(zeros((self.m,1)))self.b = 0self.eCache = mat(zeros((self.m,2))) #first column is valid flagself.K = mat(zeros((self.m,self.m)))for i in range(self.m):self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)def calcEk(oS, k):fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)Ek = fXk - float(oS.labelMat[k])return Ekdef selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs EjmaxK = -1; maxDeltaE = 0; Ej = 0oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta EvalidEcacheList = nonzero(oS.eCache[:,0].A)[0]if (len(validEcacheList)) > 1:for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta Eif k == i: continue #don't calc for i, waste of timeEk = calcEk(oS, k)deltaE = abs(Ei - Ek)if (deltaE > maxDeltaE):maxK = k; maxDeltaE = deltaE; Ej = Ekreturn maxK, Ejelse: #in this case (first time around) we don't have any valid eCache valuesj = selectJrand(i, oS.m)Ej = calcEk(oS, j)return j, Ejdef updateEk(oS, k):#after any alpha has changed update the new value in the cacheEk = calcEk(oS, k)oS.eCache[k] = [1,Ek]def innerL(i, oS):Ei = calcEk(oS, i)if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrandalphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();if (oS.labelMat[i] != oS.labelMat[j]):L = max(0, oS.alphas[j] - oS.alphas[i])H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])else:L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)H = min(oS.C, oS.alphas[j] + oS.alphas[i])if L==H: print "L==H"; return 0eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernelif eta >= 0: print "eta>=0"; return 0oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/etaoS.alphas[j] = clipAlpha(oS.alphas[j],H,L)updateEk(oS, j) #added this for the Ecacheif (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as jupdateEk(oS, i) #added this for the Ecache #the update is in the oppostie directionb1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2else: oS.b = (b1 + b2)/2.0return 1else: return 0def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMOoS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)iter = 0entireSet = True; alphaPairsChanged = 0while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):alphaPairsChanged = 0if entireSet: #go over allfor i in range(oS.m): alphaPairsChanged += innerL(i,oS)print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)iter += 1else:#go over non-bound (railed) alphasnonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]for i in nonBoundIs:alphaPairsChanged += innerL(i,oS)print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)iter += 1if entireSet: entireSet = False #toggle entire set loopelif (alphaPairsChanged == 0): entireSet = True print "iteration number: %d" % iterreturn oS.b,oS.alphas
好了,SMO的话基本就这样了,有问题的小伙伴欢迎给我留言
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!