数论——因数分解
算数基本定理/唯一分解定理
算术基本定理可表述为:任何一个大于1的自然数 N,如果N不为质数,那么N可以唯一分解成有限个质数的乘积N=P1^a1*P2^a2*P3^a3......Pn^an,这里P1<P2<P3......<Pn均为质数,其中指数ai是正整数。这样的分解称为 N 的标准分解式。最早证明是由欧几里得给出的,现代是由陈述证明。此定理可推广至更一般的交换代数和代数数论。
问题A: 求质因子及其个数
给你一个数字n ,求他的质因子及其个数
#include
#define LL long long
using namespace std;
const int MAX = 1e6+10;
const int INF = 0x3fffffff;
int a[MAX];
int an[MAX];
int num;
void Prime_num(int n){memset(a,0,sizeof(a));memset(an,0,sizeof(an));num=0;for(int i=2;i*i<=n;i++){if(n%i==0){while(n%i==0){a[num] = i;n/=i;an[num]++;}num++;}}if(n!=1){a[num] = n;an[num++] ++;}
}
int main(){int n;while(scanf("%d",&n)!=EOF){Prime_num(n);cout<<"num = "<< num< 问题B:求因子个数
先说基本定理:
若正整数n可分解为p1^a1*p1^a2*...*pk^ak其中pi为两两不同的素数,ai为对应指数,则n的约数个数为(1+a1)*(1+a2)*....*(1+ak)如180=2*2*3*3*5=2^2*3^2*5180的约数个数为(1+2)*(1+2)*(1+1)=18个。例题:给定X,Y(X, Y < 2^31),求X^Y的因子数 mod 10007。
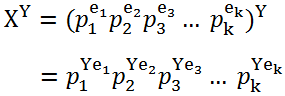
我们对问题A的代码稍加修改
#include
#define LL long long
using namespace std;
const int MAX = 1e6+10;
const int INF = 0x3fffffff;
int a[MAX];
int an[MAX];
int num;
void Prime_num(int n){memset(a,0,sizeof(a));memset(an,0,sizeof(an));num=0;for(int i=2;i*i<=n;i++){if(n%i==0){while(n%i==0){a[num] = i;n/=i;an[num]++;}num++;}}if(n!=1){a[num] = n;an[num++] ++;}
}
int main(){int n,b;while(scanf("%d%d",&n,&b)!=EOF){Prime_num(n);cout<<"num = "<< num< 问题C:求因子和
例题:给定X,Y(X, Y < 2^31),求X^Y的所有因子之和 mod 10007我们同样采取问题B 的分解方式
考虑数n,令n的因子和为s(n),对n进行素数分解后的,假设最小素数为p,素因子p的个数为e,那么n = (p^e)n'。容易得知当n的因子中p的个数为0时,因子之和为s(n')。更加一般地,当n的因子中p的个数为k的时候,因子之和为(p^k)*s(n'),所以n的所有因子之和就可以表示成:
s(n) = (1 + p^1 + p^2 + ... p^e) * s(n') = (p^(e+1) - 1) / (p-1) * s(n') s(n')可以通过相同方法递归计算。最后可以表示成一系列等比数列和的乘积。 令g(p, e) = (p^(e+1) - 1) / (p-1),则s(n) = g(p1, e1) * g(p2, e2) * ... * g(pk, ek)。#include
#define LL long long
using namespace std;
const int MAX = 1e6+10;
const int INF = 0x3fffffff;
const int MOD = 10007;
int a[MAX];
int an[MAX];
int num;
void Prime_num(int n){memset(a,0,sizeof(a));memset(an,0,sizeof(an));num=0;for(int i=2;i*i<=n;i++){if(n%i==0){while(n%i==0){a[num] = i;n/=i;an[num]++;}num++;}}if(n!=1){a[num] = n;an[num++] ++;}
}
LL pow(int a,int b){LL r = 1,base = a;while(b){if(b&1) r*=base%MOD;base*=base%MOD;b>>=1;}return r%MOD;
}
LL Prime_sum(){LL cal = 1;for(int i=0;i 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!