数据结构与算法系列----Sunday算法详解
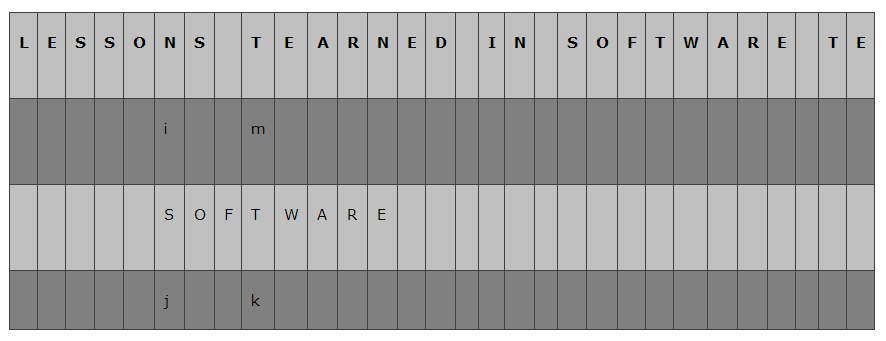
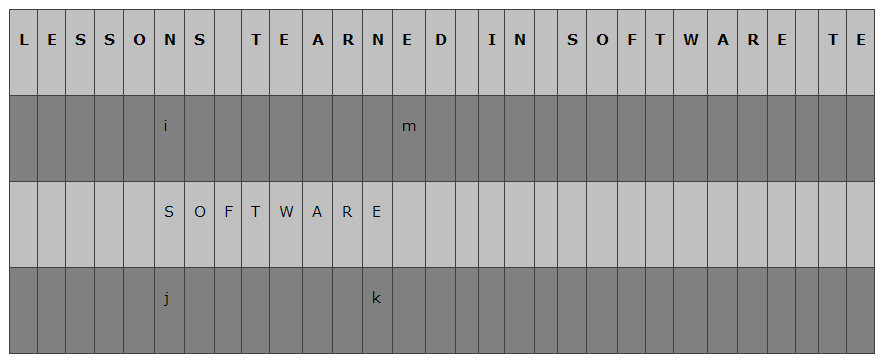
Sunday算法是Daniel M.Sunday于1990年提出的字符串模式匹配。其效率在匹配随机的字符串时比其他匹配算法还要更快。Sunday算法的实现可比KMP,BM的实现容易太多。 假设我们有如下字符串: 可以看到下图中k指向的字符与m指向的字符相等, 这时就将相等的字符对齐,让j再次指向B字符串的头一个字符,相应地,将i指向主串对应的字符N, 再次比较A[i]和B[j],不等,这时再次寻找主串中在模式串后面的那个字符, 我们看到,模式串的最后一个字符与m指向的主串字符相等,因此再次移动子串, 这时,主串i对应的字符是S,j对应的子串字符也是S,i++, j++, 现在再次不等,m指向字符"D", 返回目录---->数据结构与算法目录 参考: 图片资源采集自:符串匹配算法 – Sunday算法------->http://www.cnblogs.com/lbsong/archive/2012/05/25/2518188.html 字符串搜索算法Boyer-Moore由浅入深(比KMP快3-5倍)----->http://blog.jobbole.com/52830/ 字符串匹配的Boyer-Moore算法------>http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html 【模式匹配】之 —— Sunday算法------>http://blog.csdn.net/sunnianzhong/article/details/8820123
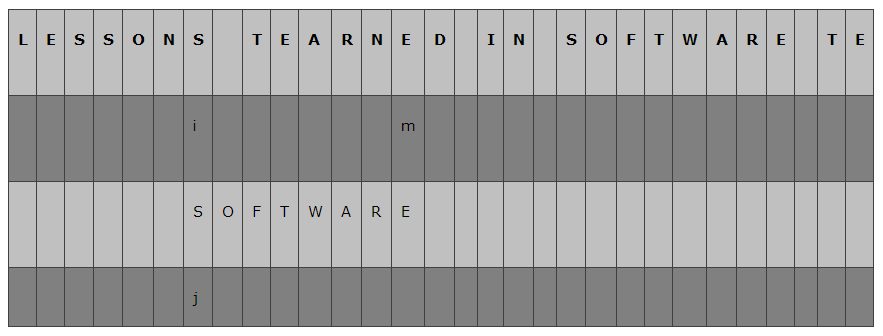
A = "LESSONS TEARNED IN SOFTWARE TE";
B = "SOFTWARE";
Sunday算法的大致原理是:
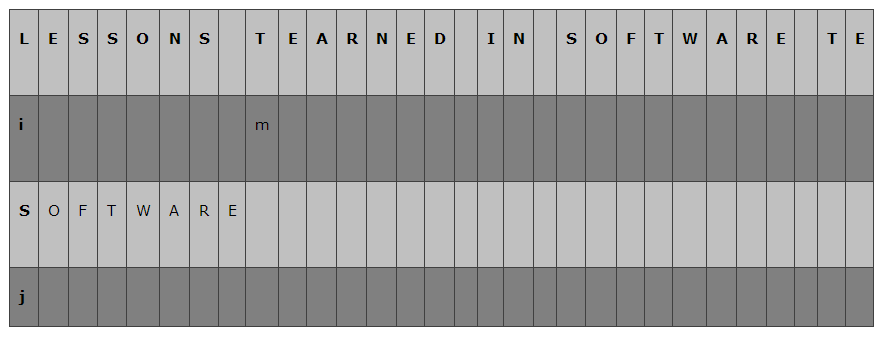
先从左到右逐个字符比较,以我们的字符串为例:
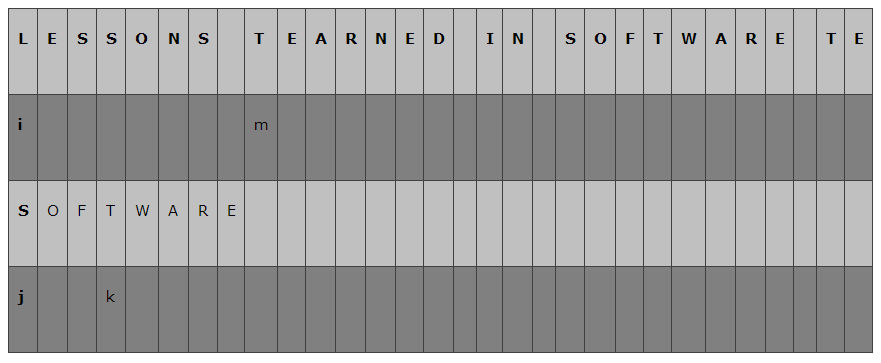
开始的时候,我们让i = 0, 指向A的第一个字符; j = 0 指向B的第一个字符,分别为"L"和"S",不等;这个时候,Sunday算法要求,找到位于A字串中位于B字符串后面的第一个字符,即下图中 m所指向的字符"T",在模式字符串B中从后向前查找是否存在"T",
#define _CRT_SECURE_NO_DEPRECATE
#define _CRT_SECURE_CPP_OVERLOAD_STANDARD_NAMES 1 #include
测试:
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!