MATLAB解方程(主要符号解法)
MATLAB求解:
分为数值求解和符号求解两种,前者诸如二分法、牛顿法、割线法,相关递推公式如下:
二分法:依次对比区间中点和两端的解,找到符合的区间。
牛顿法:
割线法:
下面主要介绍符号解法:
符号运算的操作对象主要是非数值的符号对象。
1、建立符号对象:
% x = sym('x')
% A = sym('a',[n1 ... nM])
% A = sym('a',n)
% syms var1 ... varN
% syms var1 ... varN [n1 ... nM]
% syms var1 ... varN n符号对象分为符号常量和符号变量,可以通过sym(A)来创建一个值为A的符号常量。此时A是一个单独的数值。
示例如下:
a = 0.5;
b = '0.5';
c = sym(0.5);
d = sym('0.5');
classa = class(a)
classb = class(b)
classc = class(c)
classd = class(d)结果:

2、有时,我们需要将改变已有的符号变量。
比如在整个函数框架不变的情况下,改变某一个自变量的值。
符号变量的代换和数值转换与普通的变量不同,不能直接使用等号:
syms a b
subs(a+b,a,4)syms a b
subs(cos(a)+sin(b),{a,b},{sym('alpha'),2})syms a t
subs(exp(a*t),'a',-magic(2))syms x y
subs(x*y,{x,y},{[0 1;-1 0],[1 -1;-2 1]})上述四个代码块的结果总结如下:

需要注意,当多个符号变量都需要代换时,对应的变量集合和数值集合(只是这个例子中是数值)都要用{}放在一起。
3、将符号对象转换回数值对象
使用double()函数将符号对象转换为数值对象并得到数值解
a = sym(2*sqrt(2));
b = sym((1-sqrt(3))^2);
T=[a,b]
double(T)在上面这段程序中,T代表的还是符号对象,是一个符号化的常量矩阵,double函数作用后,化为double类型的数值矩阵
结果如下:

另一种解决方法是使用vpa()函数和digits()函数配合,展示代码如下:
q = vpa(sin(sym(pi)/4))
digits(25)%此处已经修改精度为25位
p = vpa(pi)
w = vpa(sym(pi),50)
classq = class(q)
classp = class(p)
classw = class(w)两个函数配合和内嵌在vpa()函数内部这两种转换方式的含义是相同的,都是返回特定精度的数值(默认是32位)
需要注意,返回的数值类型是sym符号类型。
结果如下:

以及上述代码中sym函数内部有没有单引号也会导致结果不同,演示如下:
p = vpa(pi,32)
p = vpa('pi',32)结果:
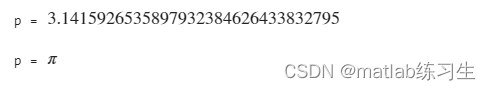
可以看出,如果用单引号,MATLAB会当做符号处理
4、运用符号变量求解代数方程
%help solve
% S = solve(eqn,var)
% S = solve(eqn,var,Name,Value)
%
% Y = solve(eqns,vars)
% Y = solve(eqns,vars,Name,Value)注意,当多变量方程求解,得到的解是一个“构架数组”。
当我们需要找到第一个解时(例),需要使用
% Y.var
下面我们求解一个三元方程组作为示例:
syms a b c x y z
[x,y,z] = solve([x*(x+y+z)-a,y*(x+y+z)-b,z*(x+y+z)-c],[x y z])av = 6;
bv = 12;
cv = 18;xv = subs(x,{a,b,c},[av bv cv])
yv = subs(y,{a,b,c},[av bv cv])
zv = subs(z,{a,b,c},[av bv cv])需要注意的是:
1、如果在赋值时不新建变量,而是直接沿用a、b、c,仍然会得到符号化的解
2、和上面演示的subs函数用法一样,在变量替换时要用{}
3、方程组和变量组的组合要用[]
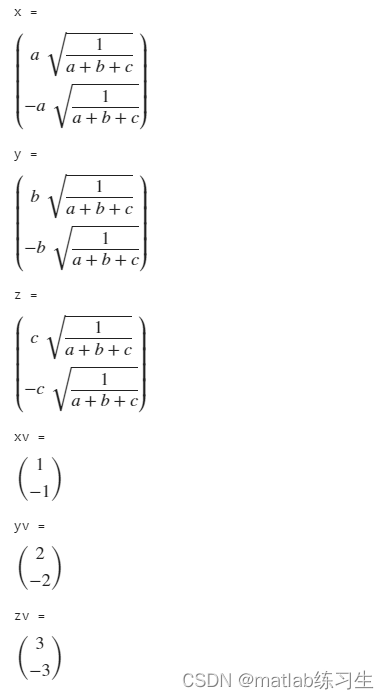
来源《高等光学仿真——光波导、激光》
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!