[NOIP2011 提高组] 铺地毯

题目：[NOIP2011 提高组] 铺地毯

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 $n$ 张地毯，编号从 $1$ 到 $n$。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入格式

输入共 $n+2$ 行。

第一行，一个整数 $n$，表示总共有 $n$ 张地毯。

接下来的 $n$ 行中，第 $i+1$ 行表示编号 $i$ 的地毯的信息，包含四个整数 $a,b,g,k$，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 $(a,b)$ 以及地毯在 $x$ 轴和 $y$ 轴方向的长度。

第 $n+2$ 行包含两个整数 $x$ 和 $y$，表示所求的地面的点的坐标 $(x,y)$。

输出格式

输出共 $1$ 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 -1。

样例 #1

样例输入 #1

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

样例输出 #1

3

样例 #2

样例输入 #2

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

样例输出 #2

-1

提示

【样例解释 1】

如下图，$1$ 号地毯用实线表示，$2$ 号地毯用虚线表示，$3$ 号用双实线表示，覆盖点 $(2,2)$ 的最上面一张地毯是 $3$ 号地毯。

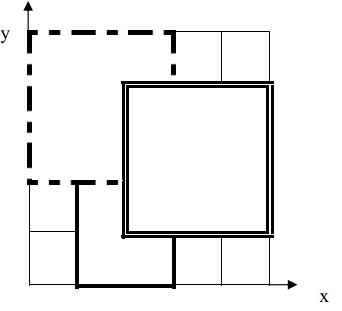
【数据范围】

对于 $30\%$ 的数据，有 $n\le 2$。
对于 $50\%$ 的数据，$0\le a,b,g,k\le 100$。
对于 $100\%$ 的数据，有 0 ≤ n ≤ 1 0 4 0 \le n \le 10^4 0≤n≤104, 0 ≤ a , b , g , k ≤ 10 5 0 \le a, b, g, k \le {10}^5 0≤a,b,g,k≤105。

noip2011 提高组 day1 第 $1$ 题。

题解

解题思路

本题是一个很简单的模拟题

因为这道题所占用的空间较大，如果进行遍历数组地图的方法无论是空间复杂度还是时间复杂度都会变得很复杂

所以，不妨进行分析，其实每个地毯只需要5个数据就好，这样能大大的加大空间利用率，也不必去遍历那些无用的空间。 每张地毯所需要的数据无非是左下角坐标x,y，右上角坐标x,y和地毯编号。 只要点在地毯范围内，最后取编号最大的输出即可。

一开始开个二维数组去搞，没看到数据范围…MLE…$(QAQ)$，换成结构体数组就$AC$了

考点

模拟 枚举

时间复杂度

$O(N)$

AC代码

#pragma GCC optimize(2) 
#include 
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar(); }while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
const int MAXN=1e5+5; 
long long n,xx,yy,di=-1;
struct dt{long long a,b,x,y;
}d[MAXN];
int main(){n=read();for(int i=1;i<=n;i++){d[i].a=read();d[i].b=read();d[i].x=read();d[i].y=read();	}xx=read();yy=read();for(int i=1;i<=n;i++){if(xx>=d[i].a&&xx<=d[i].a+d[i].x&&yy>=d[i].b&&yy<=d[i].b+d[i].y){di=i;}}printf("%lld",di);return 0;
}

[NOIP2011 提高组] 选择客栈

题目：[NOIP2011 提高组] 选择客栈

题目描述

丽江河边有 $n$ 家很有特色的客栈，客栈按照其位置顺序从 $1$ 到 $n$ 编号。每家客栈都按照某一种色调进行装饰（总共 $k$ 种，用整数 $0\sim k-1$ 表示），且每家客栈都设有一家咖啡店，每家咖啡店均有各自的最低消费。

两位游客一起去丽江旅游，他们喜欢相同的色调，又想尝试两个不同的客栈，因此决定分别住在色调相同的两家客栈中。晚上，他们打算选择一家咖啡店喝咖啡，要求咖啡店位于两人住的两家客栈之间（包括他们住的客栈），且咖啡店的最低消费不超过 $p$ 。

他们想知道总共有多少种选择住宿的方案，保证晚上可以找到一家最低消费不超过 $p$ 元的咖啡店小聚。

输入格式

共 $n+1$ 行。

第一行三个整数 $n,k,p$，每两个整数之间用一个空格隔开，分别表示客栈的个数，色调的数目和能接受的最低消费的最高值；

接下来的 $n$ 行，第 $i+1$ 行两个整数，之间用一个空格隔开，分别表示 $i $ 号客栈的装饰色调 a i a_i ai​ 和 $i$ 号客栈的咖啡店的最低消费 b i b_i bi​。

输出格式

一个整数，表示可选的住宿方案的总数。

样例 #1

样例输入 #1

5 2 3 
0 5 
1 3 
0 2 
1 4 
1 5

样例输出 #1

3

提示

样例解释

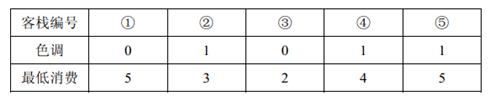
2 人要住同样色调的客栈，所有可选的住宿方案包括：住客栈①③，②④，②⑤，④⑤，但是若选择住 $4,5$号客栈的话，$4,5$ 号客栈之间的咖啡店的最低消费是 $4$ ，而两人能承受的最低消费是 $3$ 元，所以不满足要求。因此只有前 $3$ 种方案可选。

数据范围

• 对于 $30\%$ 的数据，有 $n\le 100$ ；
• 对于 $50\%$ 的数据，有 $n\le 1000$；
• 对于 $100\%$ 的数据，有 2 ≤ n ≤ 2 × 1 0 5 2 \leq n \leq 2 \times 10^5 2≤n≤2×105，$1\le k\le 50$，$0\le p\le 100$， 0 ≤ b i ≤ 100 0 \leq b_i \leq 100 0≤bi​≤100。

题解

解题思路

简单来讲就是在一段一维客栈中，任意选择两个客栈$a、b$，满足以下两个条件：

1.$a、b$颜色相同，
2. $[a,b]$闭区间之间必须存在某个客栈的咖啡店的花费小于等于$p$；

因为我们要找到所有成立的 $a、b$，那么我们就枚举每个$b$ 想办法找到此时符合条件的a有多少个

用一个变量t记录的是当前枚举客栈过程中，离我们枚举到的客栈最近的最低消费小于等于$p$的客栈的下标（第几个客栈）

开个数组$（num[]）$实时更新在t前面的各个颜色的客栈有多少个;

当然我们还用了一个$color$数组记录每个客栈的颜色，这样我们就得到了答案

考点

递推

时间复杂度

$O(N)$

AC代码

#pragma GCC optimize(2) 
#include 
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar(); }while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
const int MAXN=200005; 
long long n,k,p,t,ans,price,num[110],color[MAXN];
int main(){n=read();k=read();p=read();for(int i=1;i<=n;i++){color[i]=read();price=read();if(price<=p)		{for(int j=i;j>t;j--){num[color[j]]++;} t=i;ans+=num[color[i]]-1;}else{ans+=num[color[i]];}}printf("%lld",ans);return 0;
}

[NOIP2011 提高组] Mayan 游戏

题目：[NOIP2011 提高组] Mayan 游戏

题目描述

Mayan puzzle 是最近流行起来的一个游戏。游戏界面是一个$7$ 行 $\times 5$ 列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1. 每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图 $6$ 到图 $7$）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图 $1$ 和图 $2$）；

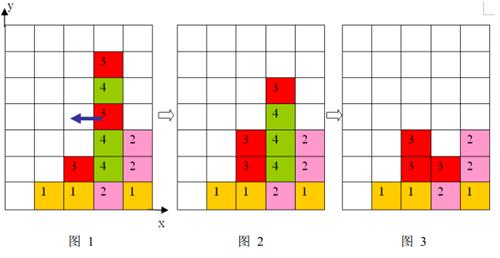
2. 任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：

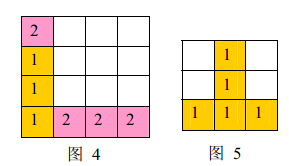
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图 $4$，三个颜色为 $1$ 的方块和三个颜色为 $2$ 的方块会同时被消除，最后剩下一个颜色为 $2$ 的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形，$5$ 个方块会同时被消除）。

3. 方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图 $1$ 到图 $3$ 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为 $(0,0)$，将位于 $(3,3)$ 的方块向左移动之后，游戏界面从图 $1$ 变成图 $2$ 所示的状态，此时在一竖列上有连续三块颜色为 $4$ 的方块，满足消除条件，消除连续 $3$ 块颜色为 $4$ 的方块后，上方的颜色为 $3$ 的方块掉落，形成图 $3$ 所示的局面。

输入格式

共 $6$ 行。

第一行为一个正整数 $n$，表示要求游戏通关的步数。

接下来的 $5$ 行，描述 $7\times 5$ 的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个 $0$ 结束，自下向上表示每竖列方块的颜色编号（颜色不多于 $10$ 种，从 $1$ 开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式

如果有解决方案，输出 $n$ 行，每行包含 $3$ 个整数 $x,y,g$，表示一次移动，每两个整数之间用一个空格隔开，其中 $(x,y)$ 表示要移动的方块的坐标，$g$ 表示移动的方向，$1$ 表示向右移动，$-1$ 表示向左移动。注意：多组解时，按照 $x$ 为第一关键字，$y$ 为第二关键字，$1$ 优先于 $-1$，给出一组字典序最小的解。游戏界面左下角的坐标为 $(0,0)$。

如果没有解决方案，输出一行 -1。

样例 #1

样例输入 #1

3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0

样例输出 #1

2 1 1
3 1 1
3 0 1

提示

【输入输出样例说明】

按箭头方向的顺序分别为图 $6$ 到图 $11$

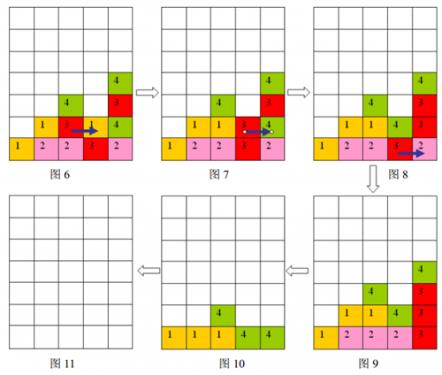
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是：$(2,1)$ 处的方格向右移动，$(3,1)$ 处的方格向右移动，$(3,0)$ 处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】

对于 $30\%$ 的数据，初始棋盘上的方块都在棋盘的最下面一行；

对于 $100\%$ 的数据，$0<n\le 5$。

题解

解题思路

此题就相当与是一道大型搜索模拟题，需要耐心，极考验码力；

因为代码比较长，所以建议大家多写函数，尽量不要都写在一起；

核心函数：

1.copy（复制）：

我们要把当前的原始状态复制，回溯时要用；但不能使用二维数组了，要定义一个三维数组last[d][i][j]，表示第d步时在i行j列的原状态；

2.update（更新游戏的状态）：
就是把该掉下去的掉下去，定义一个x为这个这个方块下0的个数，然后模拟一下；

3.remove（消除）：
题目要求一定要行或列连续3个才能消除， 但一定不能遇到3个连续的就消；

4.move （移动）：
注意，可能消除后还可以更新，所以要使用while循环；

5.check（判断是否都消除了）：
所有方块都掉落了，直接判断最后一行是否都为0；

DFS的剪枝：

相同颜色的方块可以跳过（显而易见）；
只有右边有方块才move，左边没有方块才move；

考点

模拟 搜索 剪枝

时间复杂度

O ( N 2 ) O(N^2) O(N2)

AC代码

#pragma GCC optimize(2)
#include 
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar(); }while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
const int MAXN=10;
long long n,ma[MAXN][MAXN],ans[MAXN][MAXN],last[MAXN][MAXN][MAXN],cnt[MAXN][MAXN];
bool remove(){bool flag=0;for(int i=1;i<=5;i++){for(int j=1;j<=7;j++){if(i-1>=1&&i+1<=5&&ma[i][j]==ma[i-1][j]&&ma[i][j]==ma[i+1][j]&&ma[i][j]){cnt[i-1][j]=1;cnt[i+1][j]=1;cnt[i][j]=1;flag=1;}if(j-1>=1&&j+1<=7&&ma[i][j]==ma[i][j+1]&&ma[i][j]==ma[i][j-1]&&ma[i][j]){cnt[i][j]=1;cnt[i][j+1]=1;cnt[i][j-1]=1;flag=1;}}}if(!flag){return 0;}for(int i=1;i<=5;i++){for(int j=1;j<=7;j++){if(cnt[i][j]){cnt[i][j]=0;ma[i][j]=0;} }}return 1;
}
bool check(){for(int i=1;i<=5;i++){if(ma[i][1]){return 0;}}return 1;
}
void copy(int x){for(int i=1;i<=5;i++){for(int j=1;j<=7;j++){last[x][i][j]=ma[i][j];}}
}
void update(){for(int i=1;i<=5;i++){int wow=0;for(int j=1;j<=7;j++){if(!ma[i][j]){wow++;}else{if(!wow){continue;}ma[i][j-wow]=ma[i][j];ma[i][j]=0;}}}
}
void move(int i,int j,int x){int tmp=ma[i][j];ma[i][j]=ma[i+x][j];ma[i+x][j]=tmp;update();while(remove()){update();}
}
void dfs(int x){if(check()){for(int i=1;i<=n;i++){if(i!=1){printf("\n");}for(int j=1;j<=3;j++){printf("%lld ",ans[i][j]);}}exit(0);}if(x==n+1){return;}copy(x);for(int i=1;i<=5;i++){for(int j=1;j<=7;j++){if(ma[i][j]){if(i+1<=5&&ma[i][j]!=ma[i+1][j]){move(i,j,1);ans[x][1]=i-1;ans[x][2]=j-1;ans[x][3]=1;dfs(x+1);for(int i=1;i<=5;i++){for(int j=1;j<=7;j++){ma[i][j]=last[x][i][j];}}ans[x][1]=-1;ans[x][2]=-1;ans[x][3]=-1;}}if(i-1>=1&&ma[i-1][j]==0){move(i,j,-1);ans[x][1]=i-1;ans[x][2]=j-1;ans[x][3]=-1;dfs(x+1);for(int i=1;i<=5;i++){for(int j=1;j<=7;j++){ma[i][j]=last[x][i][j];}}ans[x][1]=-1;ans[x][2]=-1;ans[x][3]=-1;}}}
}
int main(){n=read();for(int i=1;i<=5;i++){for(int j=1;j<=8;j++){long long x=read();if(x==0){break;} ma[i][j]=x;}}memset(ans,-1,sizeof(ans));dfs(1);printf("-1");return 0;
}

[NOIP2011 提高组] 计算系数

题目：[NOIP2011 提高组] 计算系数

题目描述

给定一个多项式 ( b y + a x ) k (by+ax)^k (by+ax)k，请求出多项式展开后 x n × y m x^n\times y^m xn×ym 项的系数。

输入格式

输入共一行，包含 $5$ 个整数，分别为 $a,b,k,n,m$，每两个整数之间用一个空格隔开。

输出格式

输出共一行，包含一个整数，表示所求的系数。

这个系数可能很大，输出对 $10007$ 取模后的结果。

样例 #1

样例输入 #1

1 1 3 1 2

样例输出 #1

3

提示

【数据范围】

对于 $30\%$ 的数据，有 $0\le k\le 10$。

对于 $50\%$ 的数据，有 $a=1$，$b=1$。

对于 $100\%$ 的数据，有 $0\le k\le 1000$，$0\le n,m\le k$，$n+m=k$， 0 ≤ a , b ≤ 1 0 6 0\le a,b\le 10^6 0≤a,b≤106。

noip2011 提高组 day2 第 1 题。

题解

解题思路

本题是一个很简单的数学推理题

根据二项式定理

( a + b ) n = ∑ k = 0 n C n k a k b n − k (a+b)^n=\sum_{k=0}^nC_{n}^{k}a^kb^{n-k} (a+b)n=k=0∑n​Cnk​akbn−k

那么

( a x + b y ) k = ∑ p = 0 k C k p ( a x ) p ( b y ) k − p = ∑ p = 0 k ( C k p a p b k − p ) x p y k − p (ax+by)^k=\sum_{p=0}^kC_{k}^p(ax)^p(by)^{k-p}=\sum_{p=0}^k(C_{k}^pa^pb^{k-p})x^py^{k-p} (ax+by)k=p=0∑k​Ckp​(ax)p(by)k−p=p=0∑k​(Ckp​apbk−p)xpyk−p

算 a n , b m a^n,b^m an,bm需要用快速幂

1、可以根据组合式的递推公式算组合数

C n m = C n − 1 m + C n − 1 m − 1 C_n^m=C_{n-1}^m+C_{n-1}^{m-1} Cnm​=Cn−1m​+Cn−1m−1​

2、或者是利用组合数的定义式,但是因为有取余, 所以要用逆元

C n m = n ! m o d 10007 m ! ( n − m ) ! m o d 10007 = n ! × [ m ! ( n − m ) ! ] − 1 m o d 10007 C_n^m=\frac{n!\mod 10007}{m!(n-m)!\mod 10007}=n!\times [m!(n-m)!]^{-1}\mod 10007 Cnm​=m!(n−m)!mod10007n!mod10007​=n!×[m!(n−m)!]−1mod10007

其中 [ m ! ( n − m ) ! ] − 1 [m!(n-m)!]^{-1} [m!(n−m)!]−1为逆元, 可以直接用费马小定理，最后求得$ans$的值

考点

数学

时间复杂度

$O(N!)$

AC代码

#pragma GCC optimize(2) 
#include 
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar();}while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
const int mod=10007;
const int MAXN=1e3+10;
long long a,b,k,n,m,c[MAXN][MAXN];
long long dfs(int a,int b){int ans=1;while(b){if(b&1){ans=(long long)ans*a%mod;} a=(long long)a*a%mod;b>>=1;}return ans%mod;
}
int main() {a=read();b=read();k=read();n=read();m=read();for(int i=0;i<=1000;i++){for(int j=0;j<=i;j++) {if(j==0){c[i][j]=1;}else{c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;	} }}printf("%lld",(long long)dfs(a,n)*dfs(b,m)*c[k][n]%mod);return 0;
}

[NOIP2011 提高组] 聪明的质监员

题目：[NOIP2011 提高组] 聪明的质监员

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 $n$ 个矿石，从 $1$ 到 $n$ 逐一编号，每个矿石都有自己的重量 w i w_i wi​ 以及价值 v i v_i vi​ 。检验矿产的流程是：

1 、给定$ m$ 个区间 [ l i , r i ] [l_i,r_i] [li​,ri​]；

2 、选出一个参数 $W$；

3 、对于一个区间 [ l i , r i ] [l_i,r_i] [li​,ri​]，计算矿石在这个区间上的检验值 y i y_i yi​：

y i = ∑ j = l i r i [ w j ≥ W ] × ∑ j = l i r i [ w j ≥ W ] v j y_i=\sum\limits_{j=l_i}^{r_i}[w_j \ge W] \times \sum\limits_{j=l_i}^{r_i}[w_j \ge W]v_j yi​=j=li​∑ri​​[wj​≥W]×j=li​∑ri​​[wj​≥W]vj​

其中 $j$ 为矿石编号。

这批矿产的检验结果 $y$ 为各个区间的检验值之和。即： ∑ i = 1 m y i \sum\limits_{i=1}^m y_i i=1∑m​yi​

若这批矿产的检验结果与所给标准值 $s$ 相差太多，就需要再去检验另一批矿产。小T 不想费时间去检验另一批矿产，所以他想通过调整参数 $W$ 的值，让检验结果尽可能的靠近标准值 $s$，即使得 $|s-y|$ 最小。请你帮忙求出这个最小值。

输入格式

第一行包含三个整数 $n,m,s$，分别表示矿石的个数、区间的个数和标准值。

接下来的 $n$ 行，每行两个整数，中间用空格隔开，第 $i+1$ 行表示 $i$ 号矿石的重量 w i w_i wi​ 和价值 v i v_i vi​。

接下来的 $m$ 行，表示区间，每行两个整数，中间用空格隔开，第 $i+n+1$ 行表示区间 [ l i , r i ] [l_i,r_i] [li​,ri​] 的两个端点 l i l_i li​ 和 r i r_i ri​。注意：不同区间可能重合或相互重叠。

输出格式

一个整数，表示所求的最小值。

样例 #1

样例输入 #1

5 3 15 
1 5 
2 5 
3 5 
4 5 
5 5 
1 5 
2 4 
3 3

样例输出 #1

10

提示

【输入输出样例说明】

当 $W$ 选 $4$ 的时候，三个区间上检验值分别为 $20,5,0$ ，这批矿产的检验结果为 $25$，此时与标准值 $S$ 相差最小为 $10$。

【数据范围】

对于 $10\%$ 的数据，有 $1\le n,m\le 10$；

对于 $30\%$的数据，有 $1\le n,m\le 500$ ；

对于 $50\%$ 的数据，有 $1\le n,m\le 5,000$；

对于 $70\%$ 的数据，有 $1\le n,m\le 10,000$ ；

对于 $100\%$ 的数据，有 $1\le n,m\le 200,000$， 0 < w i , v i ≤ 1 0 6 0 < w_i,v_i≤10^6 0<wi​,vi​≤106， 0 < s ≤ 1 0 12 0 < s≤10^{12} 0<s≤1012， 1 ≤ l i ≤ r i ≤ n 1 ≤l_i ≤r_i ≤n 1≤li​≤ri​≤n 。

题解

解题思路

这个题很明显的二分枚举，但是还有一个前缀和有点坑人。

这题题其实点不多，就两个关键点：

1、二分的判断。

可以看到：在W取0时，所有的区间内的矿石都可以选上，而在W大于最大的质量时，所有的矿石都选不上。

然后简单算一下就发现：

W越大，矿石选的越少，W越小，矿石选的越多。

所以，随着W增大，Y值减小；

二分的判断条件出来了：

当$Y>s$时，需要增大$W$来减小$Y$，从而$\mid Y-s\mid$变小；

当$Y==s$时，$\mid Y-s\mid ==0$；

当$Y<s$时，需要减小$W$来增大$Y$，从而$\mid Y-s\mid$变大；

#pragma GCC optimize(2) 
#include 
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar();}while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
const int MAXN=200010;
long long w[MAXN],v[MAXN],l[MAXN],r[MAXN];
long long pre_n[MAXN],pre_v[MAXN];
long long Y,s,sum,n,m,mx=-1,mn=2147483647;
bool check(int W){	Y=0,sum=0;memset(pre_n,0,sizeof(pre_n));memset(pre_v,0,sizeof(pre_v));for(int i=1;i<=n;i++){if(w[i]>=W){pre_n[i]=pre_n[i-1]+1;pre_v[i]=pre_v[i-1]+v[i];}else{pre_n[i]=pre_n[i-1];pre_v[i]=pre_v[i-1];}}for(int i=1;i<=m;i++){Y+=(pre_n[r[i]]-pre_n[l[i]-1])*(pre_v[r[i]]-pre_v[l[i]-1]);}sum=llabs(Y-s);if(Y>s){return true;}else{return false;}
}
int main(){n=read();m=read();s=read();for(int i=1;i<=n;i++){w[i]=read();v[i]=read();mx=max(mx,w[i]);mn=min(mn,w[i]);	}for(int i=1;i<=m;i++){l[i]=read();r[i]=read();}long long left=mn-1,right=mx+2,mid; long long ans=0x3f3f3f3f3f3f3f3f;while(left<=right){mid=(left+right)>>1;if(check(mid)){left=mid+1;}else{right=mid-1;}if(sum<ans){ans=sum;}}printf("%lld",ans);return 0;
} 

3 3 2
1 4
0 1 3
1 1 2
5 2 3

10

#pragma GCC optimize(2) 
#include 
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar();}while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
const int MAXN=10005;
long long n,m,k,ans;
long long t[MAXN],tt[MAXN],l[MAXN],r[MAXN];
long long ww[MAXN],ss[MAXN],ti[MAXN],g[MAXN];
int main(){n=read();m=read();k=read();for(int i=1;i<n;i++){t[i]=read();}for(int i=1;i<=m;i++){tt[i]=read();l[i]=read();r[i]=read();}for(int i=1;i<=m;i++){ww[l[i]]=max(ww[l[i]],tt[i]);ss[r[i]]++;}for(int i=1;i<=n;i++){ss[i]=ss[i-1]+ss[i];}for(int i=2;i<=n;i++){ti[i]=max(ww[i-1],ti[i-1])+t[i-1];}for(int i=1;i<=m;i++){ans+=ti[r[i]]-tt[i];}if(!k){printf("%lld\n",ans);return 0;}while(k--){g[n]=n;g[n-1]=n;for(int i=n-2;i>=1;i--){if(ti[i+1]<=ww[i+1]){g[i]=i+1;}else{g[i]=g[i+1];}}long long maxn=0,maxw=0;for(int i=1;i<n;i++){if(ss[g[i]]-ss[i]>maxn&&t[i]>0){maxn=ss[g[i]]-ss[i];maxw=i;}}t[maxw]--;ans-=maxn;for(int i=1;i<=n;i++){ti[i]=max(ww[i-1],ti[i-1])+t[i-1];}}printf("%lld\n",ans);return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！