稀疏编码学习笔记（1）

一、起源于发展

稀疏编码起源于神经生物学，简单来说，从视网膜到大脑皮层存在一系列细胞,将视野感知的数据量极大的图片，以极小的代价去代表和存储，每个神经元对这些外部刺激的表达则采用了稀疏编码(Sparse Coding, SC)原则,将图像在边缘、端点、条纹等方面的特性以稀疏编码的形式进行描述.

1988年,Michison明确提出了神经稀疏编码的概念。

1989年,Field提出了稀疏分布式编码(Sparse Distributed Coding)方法.这种编码方法并不减少输入数据的维数,而是使响应于任一特殊输入信息的神经细胞数目被减少,信号的稀疏编码存在于细胞响应分布的四阶矩(即峭度Kurtosis)中.

1996年,Olshausen和Field在Nature杂志上发表了一篇重要论文指出,自然图像经过稀疏编码后得到的基函数类似于V1区简单细胞感受野的反应特性.这种稀疏编码模型提取的基函数首次成功地模拟了V1区简单细胞感受野的三个响应特性:空间域的局部性、时域和频域的方向性和选择性.考虑到基函数的超完备性(基函数维数大于输出神经元的个数),Olshausen 和Field在1997年又提出了一种超完备基的稀疏编码算法,利用基函数和系数的概率密度模型成功地建模了V1区简单细胞感受野.

1997年,Bell和Sejnowski 等人把多维独立分量分析(Independent Component Analysis, ICA)用于自然图像数据分析,并且得出一个重要结论:ICA实际上就是一种特殊的稀疏编码方法.

稀疏编码存储能力大，计算简单，在盲源信号分离、语音信号处理、特征提取、自然图像去噪以及模式识别等方面都有广泛应用。

我本人学习该算法是为了提取点云数据的特征做分类。

稀疏编码的主要问题：求解最优化目标函数（完备基函数）

二、相关概念

有几个重要的基础概念先说明：

（1）我们要找一个输入量X的一种稀疏表示，要求该表示尽可能与输入量的特征相似，并且系数稀疏。由线性代数的知识可知：稀疏系数可以得到无穷解，在所有的可行解中挑出非零元素最少的解，也就是满足稀疏性。L0（0范数，向量中非0的元素的个数）是来规范系数矩阵是否稀疏的一个标准，但是由于L0很难优化求解（在0处不可微）。

（2）Terry tao证明了，在满足一定条件下，L0问题与L1问题是等价的，L1范数是指向量中各个元素绝对值之和，L0范数的最优凸近似，而且它比L0范数要容易优化求解，所以用L1来实现稀疏。

（3）作为一个模型，L2范数（向量各元素的平方和然后求平方根）可以防止过拟合，提升模型的泛化能力。 我们让L2范数的规则项||W||2最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，L1让它等于0。L2同时可以处理条件数不好的情况下矩阵求逆很困难的问题（条件数：矩阵稳定性的度量值，如果在1附近就是稳定，远大于1输出结果不可信），可以让优化求解变的稳定快速。

稀疏编码算法是一种无监督学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。稀疏编码算法的目的就是找到一组基向量 ϕi ，使得我们能将输入向量 x表示为这些基向量的线性组合：

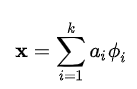
超完备基的好处是它们能更有效地找出隐含在输入数据内部的结构与模式。对于超完备基来说，系数 ai 不再由输入向量唯一确定。因此，在稀疏编码算法中，需要另加了一个评判标准“稀疏性（sparsity ）”来解决因超完备（over-completeness）而导致的退化（degeneracy）问题。

Sparse Coding是将输入数据重构为一组超完备基向量的线性组合，然后这些基向量前面的系数所构成的向量就是输入数据的新特征。

Sparse Coding在实际使用过程中速度很慢，这是因为即使我们在训练阶段已经把输入数据集的超完备基学习到了，在测试阶段时还是要通过凸优化的方法去求得其特征值（即基组合前面的系数值），所以这比一般的前向神经网络速度要慢。　

马毅教授研究组在NeurIPS 2022上发表了一篇新论文，回顾了稀疏卷积模型在图像分类中的应用，并成功解决了稀疏卷积模型的经验性能和可解释性之间的不匹配问题。

文中提出的可微优化层使用卷积稀疏编码（CSC）对标准卷积层进行替换。

结果表明，与传统的神经网络相比，这些模型在 CIFAR-10、 CIFAR-100和 ImageNet 数据集上具有同样强的经验性能。

通过利用稀疏建模的稳定恢复特性，研究人员进一步表明，只需要在稀疏正则化和数据重构项之间进行简单的适当权衡，这些模型就可以对输入损坏以及测试中的对抗性扰动具有更强的鲁棒性。

也就是说，在无监督学习中，神经网络的黑盒特性，虽然有很好的经验性，但是由于其不确定性，我们可能没办法解释和干扰其中的迭代过程。但是稀疏编码做深度网络时，每一层的功能完全透明，更好解释和修改网络层。

稀疏编码更适合分类问题和生成模型。

三、公式推理

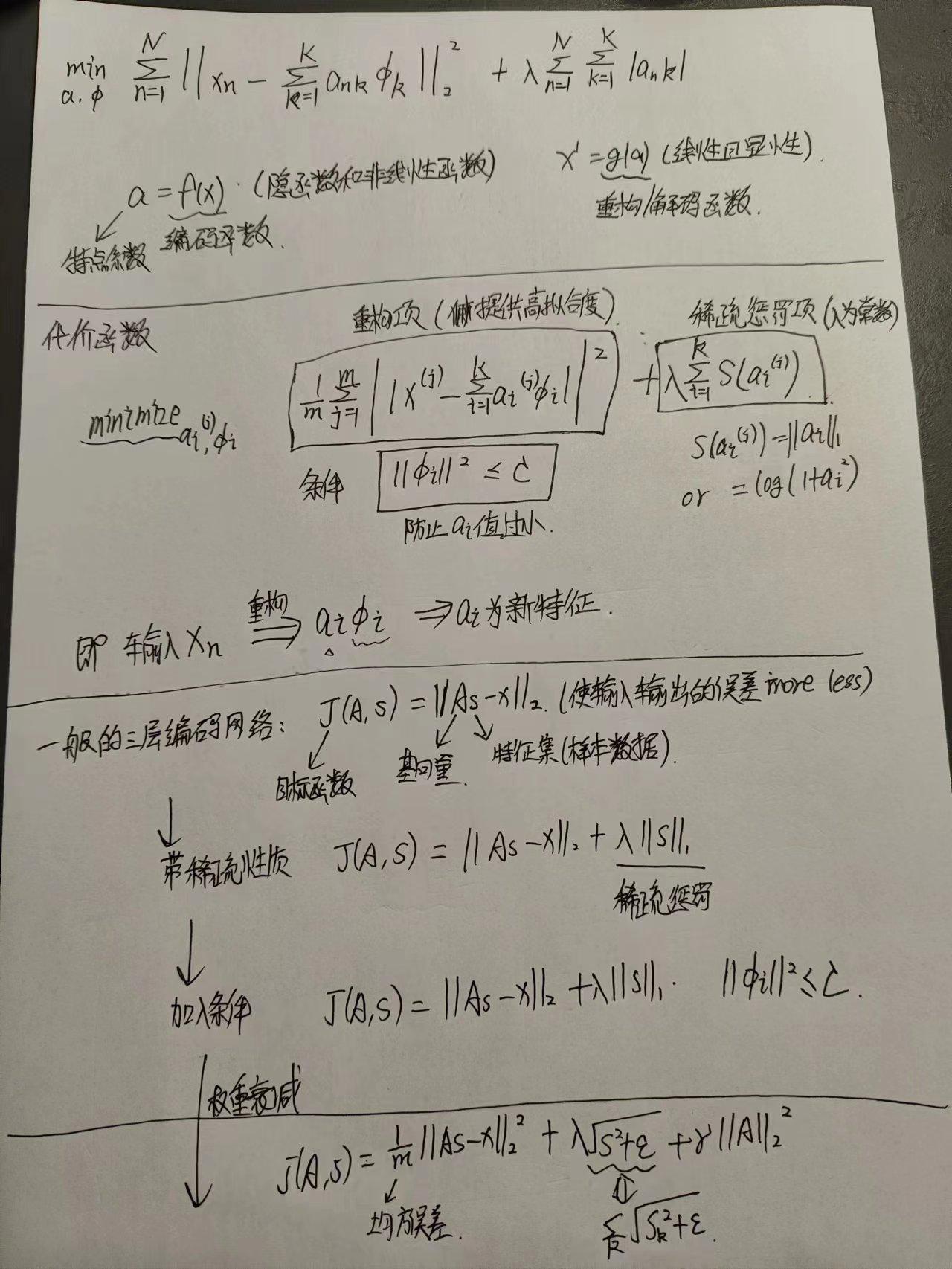
如果只有前面两项（重构代价项和稀疏惩罚项），那么就存在一个问题： 如果将系数向量s中各项系数值减到很小，且将字典A中每个基向量的值增加到很大，这样第一项的代价值基本保持不变，而第二项的稀疏惩罚值却会相应变小。也就是说只要将所有系数都减小同时基向量的值增大，那么就能最小化上面的代价函数。在这种情况下，所有的系数a都变得很小，即：它们都大于0但接近于0，而这并不满足我们对系数向量的稀疏性要求：系数向量s中只有少数系数远远大于0，而不是大部分系数都接近于0。

　　所以为了防止这种情况发生，我们需要保证字典A中基向量的元素值都不会变得太大，这就是权重衰减项的意义。

L1 范数在 0 点处不可微影响了梯度方法的应用。尽管可以通过其他非梯度下降方法避开这一问题，但是本文通过使用近似值“平滑” L1 范数的方法解决此难题。 对 L1 范数进行平滑，其中 ε 是“平滑参数”（”smoothing parameter”）或者“稀疏参数”（”sparsity parameter”） （如果 ε远大于x, 则 x + ε 的值由 ε 主导，其平方根近似于ε）。在下文提及拓扑稀疏编码时，“平滑”会派上用场。

稀疏编码算法涉及超完备基Φ（字典）和系数向量a的学习，因此训练是由两个独立的优化过程组合起来的。每次迭代分两步：第一个是固定字典Φ，逐个使用训练样本x来优化系数 ai ，第二个是固定系数向量a，一次性处理多个样本对字典Φ进行优化。不断迭代，直至收敛，这就可以得到一组能够良好表示训练样本x的超完备基，也就是字典。

关于系数向量a的优化：

　　(1) 使用 L1 范式作为稀疏惩罚函数，对 a(j)i的学习过程就简化为求解“由 L1 范式正则化的最小二乘法问题”，这个问题函数在域 a(j)i内为凸，已经有很多技术方法来解决这个问题。

　　(2) 使用对数形式的稀疏惩罚函数，则可以采用基于梯度算法的方法，如共轭梯度法。

关于字典Φ的优化：

　　使用 L2 范式约束来学习基向量，同样可以简化为一个带有二次约束的最小二乘问题，其问题函数在域 Φ 内也为凸。

优化迭代过程：

　1. 随机初始化A

　　2. 重复以下步骤直至收敛：

　　　　a. 根据上一步给定的A，求解能够最小化J(A,s)的s （由L1范式正则化的最小二乘法问题或采用基于梯度算法的方法，如共轭梯度法）

　　　　b. 根据上一步得到的s，求解能够最小化J(A,s)的A（简化为一个带有二次约束的最小二乘问题，比如求解拉格朗日对偶函数）

稀疏编码的一些变种：

黎曼稀疏编码

结构化稀疏编码

稀疏线性编码

稀疏自编码

概率稀疏编码

四、稀疏编码字典的学习和选择？

《Dictionary Learning for Sparse Coding:Algorithms and Convergence Analysis》

问题：

（1）不可能提取每个点云的特征，所以稀疏编码的输入向量如何界定？

意味着在提取特征之前就要给点云进行粗分类，划分点簇，提取点簇的特征。

（2）点云簇如何划分？

设想使用图论，将每个点云的K近邻构成无向图，作为输入向量。但是遇到连接组件（大汽车旁边有人）就分不出组件中的单独对象，可能到最后根本识别不到小目标，也就是说即使构成了无向图，也要重新进行切割图。

（3）图如何切割？如何划分连通分量？簇中点云数量上下限怎么定？

（4）小目标检测目前的难点：

大规模的通用小目标数据集尚处于缺乏状态，现有的算法没有足够的先验信息进行学习，导致了小目标检测性能不足。此外还有容易被漏检，或者聚集区域的小目标之间边界框距离过近，还将导致边界框难以回归，模型难以收敛。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！