八大排序的实现
一:插入排序
插入排序是一种简单直观的排序方法,其基本思想在于每次将一个待排序记录,按其关键字大小插入到前面已经排序好的子序列中,直至全部记录插入完成。
由此引申三种重要排序:直接插入排序,折半插入排序,希尔排序
1:直接插入排序
1)查找A[i]在A[1...i-1]中的位置k
2)A[k...i-1]中所有元素后移一位
3)将A[i]复制到A[k]
void InsertSort(int A[],int n){int i,j;for(i=2;i<=n;i++){ //依次将A[2...n]插入到前面已经排好的序列 if(A[i].key空间复杂度:O(1)
时间复杂度:n-1趟插入插入,每趟操作都分为比较关键词和移动元素,而比较关键词和移动元素取决于待排序表的初始状态。最好情况——表中元素有序,此时只需比较,无需移动,时间复杂度为O(n),而平均时间复杂度O(n^2)
稳定性:稳定
适用性:适用于顺序存储和链式存储的线性表(PS:大部分排序算法都仅适用于顺序存储的线性表)
2:折半插入排序
对直接插入排序做适当改进即可,在查找有序子表时进行折半查找即可
void InsertSort(int A[],int n){int i,j,low,mid,high;for(i=2;i<=n;i++){ //依次将A[2...n]插入到前面已经排好的序列 A[0]=A[i] ;//将A[i]缓存在A[0];low=i,high=i-1; while(low<=high){ mid=(low+high)/2; //取中间点 if(A[mid].key>A[0].key) low=mid-1; //查左子表 else high=mid+1;//查右子表 }//(low>high跳出)for(j=i-1;j>=high+1;j--)A[j+1]=A[j];A[high+1]=A[0]; //插入操作 }
}显然,折半插入仅仅减少了比较的次数,约为O(nlogn),比较次数与待排序表的初始状态无关,仅取决于表中元素个数n。
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:稳定
3:希尔排序
上面讲解可以看出,直接插入排序算法适用于基本有序的排序表和数量不大的排序表。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
1)插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
2)但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
基本思想:
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2
对顺序表做希尔排序,与直接插入排序的相比较:
1)前后记录位置的增量是dk,不是1
void BubbleSort(int A[],int n){//升序为例for(int i=0;i=0;j--){ if(A[j-1].key>A[j].key)swap(A[j-1],A[j]) ; //逆序则交换flag=true; }if(flag==false) return ; //本趟未交换,则表已经有序,return}
} 时间复杂度:O(1)
空间复杂度:最好O(n)(表有序),平均O(n^2)
稳定性:显然是稳定的
2:快速排序
快排是对冒泡排序的改进,思想是基于分治的:
1)在待排表A[1...n]中取一个元素pivot为基准,
2)待排表元素小于pivot放A[1..K-1], 待排表元素大于等于pivotA[k+1..n],pivot元素放在最终位
这个过程称为一趟快排,然后对两子表递归的进行上述过程,直到每部分只有一个元素或为空为止
#include //不稳定排序
#include
using namespace std;
const int maxn=100;
void Quicksort(int *a,int left,int right){if(left>right) return ;int i=left,j=right;int temp=a[left];//主元 while(i!=j){ while(i=temp) j--;while(i=pivot) high--;A[low] =A[high];while(lowmaxn) n=maxn;printf("Please input the number of numbers you want to sort:\n");while(~scanf("%d",&n)){for(int i=0;i 测试用例截图:
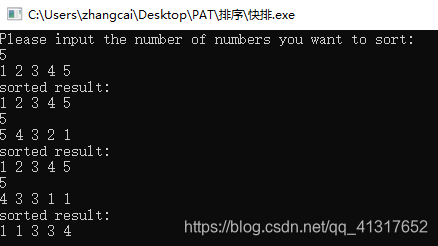
分析:
时间复杂度:快排的运行时间与划分是否对称有关,最坏情况是初始排列表基本有序或者基本逆序,此时时间复杂度为O(n^2),平均时间复杂度O(nlogn)
空间复杂度:快排是递归的,需要借助一个递归栈来保存每一层递归调用必要信息,其容量与递归深度一致,最坏情况进行n-1次递归调用,栈深度为O(n),平均栈深度O(logn).因此空间复杂度最坏O(n),平均O(logn)
稳定性:不稳定。例如A={3,2,2},一趟快排后 A={3,2,2},最终排序序列也为A={2,2,3}
注意:在快速排序中,每一趟并不产生有序子列,但每一趟后将一个元素(基准元素)放到最终位置。
三:选择排序
1:简单选择排序
基本思想:每一趟(例如第i趟)在后面n-i+1个待排序元素中选取最小的关键字元素,最为有序子列的第i个元素,n-1趟可排序完成。
//简单选择排序
void SelectSort(int A[],int n){for(int i=0;i时间复杂度:元素间的比较次数与序列初始状态无关,始终为n(n-1)/2,所以时间复杂度为O(n^2)
空间复杂度:O(1)
稳定性:不稳定,例如A={2,2,1},最终排序结果为A={1,2,2},含有相同关键字的元素相对位置发生变化。
2:堆排序(划重点)
/*
* 堆排序是一种复杂度为Nlog(N)的排序算法。对应二叉堆。
* 二叉堆是一颗完全二叉树,一般可以直接用数组实现。它的特点:
* 1. 父节点的键值总是大于等于(或小于等于)任何一个子节点的值。
* 2. 每一个节点的左右子树都是一个二叉堆。
* 当父节点的值都大于等于子节点的值,这样的二叉堆叫做大顶堆。
* 当父节点的值都小于等于子节点的值,叫做小顶堆
*/
以大根堆为例:
#include
#include
using namespace std;
const int maxn=100;void AdjustDown(int A[],int k,int len){//函数AdjustDown()将元素k向下进行调整A[0]=A[k]; //A[0]暂存for(int i=2*k;i<=len;i*=2){if(iA[i]) break; //筛选结束else{A[k]=A[i]; //将A[i]调整到双亲结点 k=i; //修改k值,继续向下调整 } }//forA[k]=A[0]; //被筛选结点放到最终位置
}void BuildMaxhead(int A[],int len){for(int i=len/2;i>0;i--) //从i=A[n/2]~1,反复调整AdjustDown(A,i,len);
} void HeadSort(int A[],int len){BuildMaxhead(A,len); //初始建堆for(int i=len;i>1;i--){ //n-1趟交换和建堆过程swap(A[i],A[1]); AdjustDown(A,1,i-1);//把剩余i-1个元素整理成堆}
} int main(){int n;int a[maxn];if(n>maxn) n=maxn;printf("Please input the number of numbers you want to sort:\n");while(~scanf("%d",&n)){for(int i=1;i<=n;i++)scanf("%d",&a[i]);HeadSort(a,n);printf("sorted result:\n");for(int i=1;i<=n;i++)printf("%d ",a[i]);}return 0;
} 测试用例截图: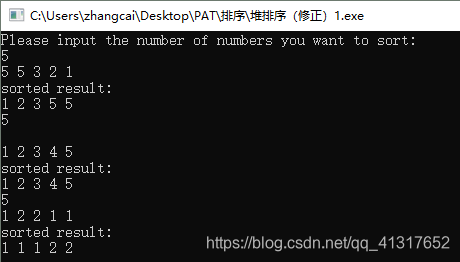
分析:
时间复杂度:建堆时间O(n),之后有n-1次向下调整,向下调整复杂度O(h),最好、最坏、平均时间复杂度都是O(nlogn)
空间复杂度:O(1)
稳定性:不稳定
注意:每一趟都能将一个元素放在最终位置
四:归并排序和基数排序
1:归并排序
核心思想:通过先递归的分解数列,再合并数列就完成了归并排序。
假定排序表有n个记录,则可看作是n个有序的子表,每个字表长度为一,然后两两归并,得到[n/2](向上取整)个长度为2或为1的有序表;两两归并.....如此重复,直至合并为一个长度为n的有序表,这种排序为二路归并。
例如:
初始关键字 49 38 65 97 76 13 27
一趟后: 38 49 65 97 13 76 27
两趟后: 38 49 65 97 13 27 76
三趟后: 13 27 38 49 65 76 97
以二路归并为例:
//归并排序
//通过先递归的分解数列,再合并数列就完成了归并排序。
#include
#include
using namespace std;
int n;
int *B=(int *)malloc((n+1)*sizeof(int));// 辅助数组
void Merge(int A[],int low,int mid,int high){for(int i=low;i<=high;i++){B[i]=A[i];}int i,j,k;for( i=low,j=mid+1,k=i;i<=mid && j<=high;k++){if(B[i]<=B[j]) //比较 B 的左右两段 ,稳定排序 ,谁小放谁 A[k]=B[i++];else A[k]=B[j++];}//跳出时左半段走完或者右半段走完 while(i<=mid) A[k++]=B[i++];while(j<=high) A[k++]=B[j++];
}void MergeSort(int A[],int low,int high){if(low>n;int A[n]; for(int i=0;i>A[i];MergeSort(A,0,n-1);for(int i=0;i 测试用例截图:

分析:
时间复杂度:每一趟归并时间复杂度O(n),共进行logn(以2为底,向上取整)趟。因此时间复杂度O(nlogn)
空间复杂度:O(n)
稳定性:Merge()不改变相同关键字记录的相对次序,因此是稳定的
注意:一般而言,对与N个元素进行K-路归并排序时,排序趟数m满足K^m=N,从而m=logk N(m为整书,结果向上取整)
2:基数排序
采用多关键字排序(基于关键字各位的大小进行排序),借助“分配”和“收集”两种操作对关键字进行排序
代码后续给出!!!
时间复杂度:O(d(n+r)),与序列初始状态无关
空间复杂度:一趟排序需要存储空间r(r个队列),以后重复使用,所以空间复杂度O(r)
复杂度总结:
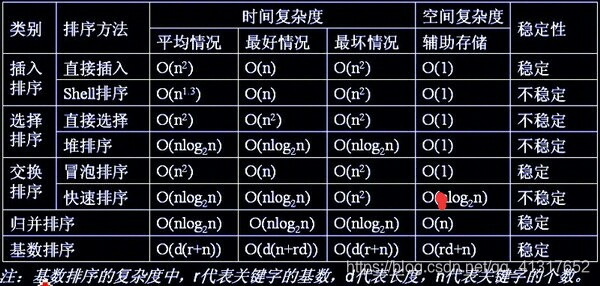
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!