matlab+pca与svd,浅谈 PCA与SVD

前言

在用数据对模子举行训练时，通常会遇到维度过高，也就是数据的特征太多的问题，有时特征之间还存在一定的相关性，这时若是还使用原数据训练模子，模子的精度会大大下降，因此要降低数据的维度，同时新数据的特征之间还要保持线性无关，这样的方式称为主身分剖析(Principal component analysis，PCA)，新数据的特征称为主身分，获得主身分的方式有两种：直接对协方差矩阵举行特征值剖析和对数据矩阵举行奇异值剖析(SVD)。

一、主身分剖析基本思想

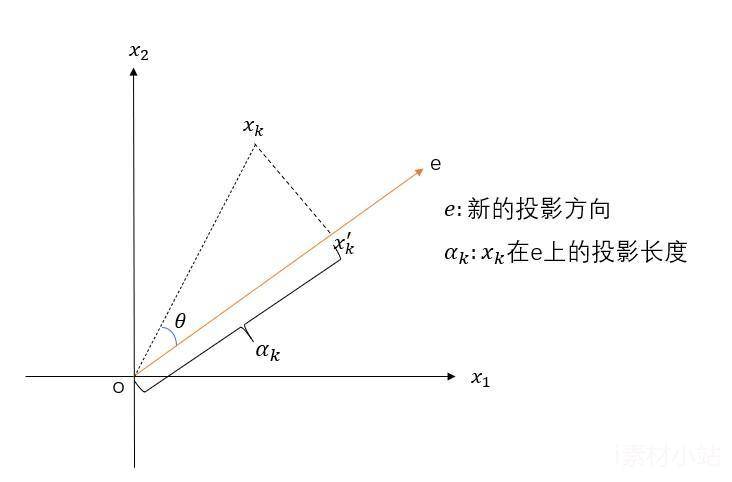
数据X由n个特征降维到k个特征，这k个特征保留最大信息(方差)。对原坐标系中的数据举行主身分剖析等价于举行坐标系的旋转转变，将数据投影到新的坐标系下，新坐标系的第一坐标轴示意第一主身分，第二坐标轴示意第二主身分，以此类推。数据在每一轴上的坐标值的平方示意响应变量的方差，PCA的目的就是方差最大的变量，才气保留尽可能多的信息，由于方差越大，示意数据涣散水平越大，所包罗的信息也就越多。

二、PCA的基本步骤

step1：对数据举行规范化(也称为标准化)，由于涉及距离盘算，因此要消除量纲的影响；

这里的数据标准化接纳z-score：X = X – mean(X) / std(X)

step2：对数据X举行旋转转变(前言提到的两

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！