二叉树（递归应用+建树）

由上一个部分可知二叉树基础，现在看看二叉树的一些应用；

目录

 计算root为根的二叉树结点个数(了解后序遍历的基础)

求树的高度或深度(后序遍历)

如何把前、中、后序递归算法的最后一条递归调用语句消除呢？教材习题248的25题

寻找树的先序中序后序遍历的第k个节点（原理都差不多）

交换左右子树(前序)

根据前中后序进行建树

（前pre+中in）代码 

(中in+后post)代码

只根据一种序列进行建树

只根据前序遍历建树

只根据中序遍历建树

只根据后序遍历建树

n个结点的完全二叉树存放在二叉树的顺序存储结构中，编写非递归算法对该树进行中序遍历。

实现一棵二叉树复制的算法。 

二叉树的所有叶子结点从左向右链接成单链表的算法 

 计算root为根的二叉树结点个数(了解后序遍历的基础)

int ListNode::Size(ListNode *root)const{if(root==NULL)return 0;elsereturn 1 + Size(root->left)+Size(root->right);
};

求树的高度或深度(后序遍历)

int ListNode::Height(ListNode *root)const{if(root==NULL)return 0;else{int i=Height(root->left);int j=Height(root->right);return ( i < j ) ? j+1,i+1;}
};

如何把前、中、后序递归算法的最后一条递归调用语句消除呢？教材习题248的25题

//前序
while (NULL != proot ){visit(proot);pretraversal(proot->lchild,visit);proot = proot ->rchild ;//类似于链表的p= p->next;}//中序
while (NULL != proot ){pretraversal(proot->lchild,visit);visit(proot);proot = proot ->rchild ;//类似于链表的p= p->next;}

把整颗树，看成是一个单链表，链表的的下一个节点是当前节点的右子女节点。

不妨设这些链表节点为编号1..X;这些节点显然是该树的一直沿着右子树的一条路径中的节点。

void binTree::posttraversal (TreeNode * proot,Visitor &visit)
{stack s;while (NULL != proot )//后序遍历TL1,TL2, ...TLx，并依次入栈1..X节点{s.push(root);posttraversal(proot->lchild,visit);proot = proot ->rchild ;//类似于链表的p= p->next;}while(!s.empty() )//按照X ..., 1次序访问节点{visit(s.top());	s.pop();}}

寻找树的先序中序后序遍历的第k个节点（原理都差不多）

看大佬博客了

(8条消息) 按先序次序建立一棵二叉树,输出中序遍历结果的倒数第K个结点值_DYSunStar的博客-CSDN博客

交换左右子树(前序)

void SwapSubTree(ListNode *root)
{ListNode *temp;if (root){temp = root->lchild;root->lchild = root->rchild;root->rchild = temp;SwapSubTree(&((*T)->lchild));SwapSubTree(&((*T)->rchild));}
}

LeetCode

​​​​​​力扣

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if(root==NULL)return root;TreeNode *temp;temp=root->left;root->left=root->right;root->right=temp;root->left=invertTree(root->left);root->right=invertTree(root->right);return root;}
};

根据前中后序进行建树

原理：二叉树面试题：前中序求后序、中后序求前序 - 万猫学社 - 博客园

前序+中序建树

力扣https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

前序+后序建树

力扣https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/

中序+后序建树

 力扣https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

（前pre+中in）代码 

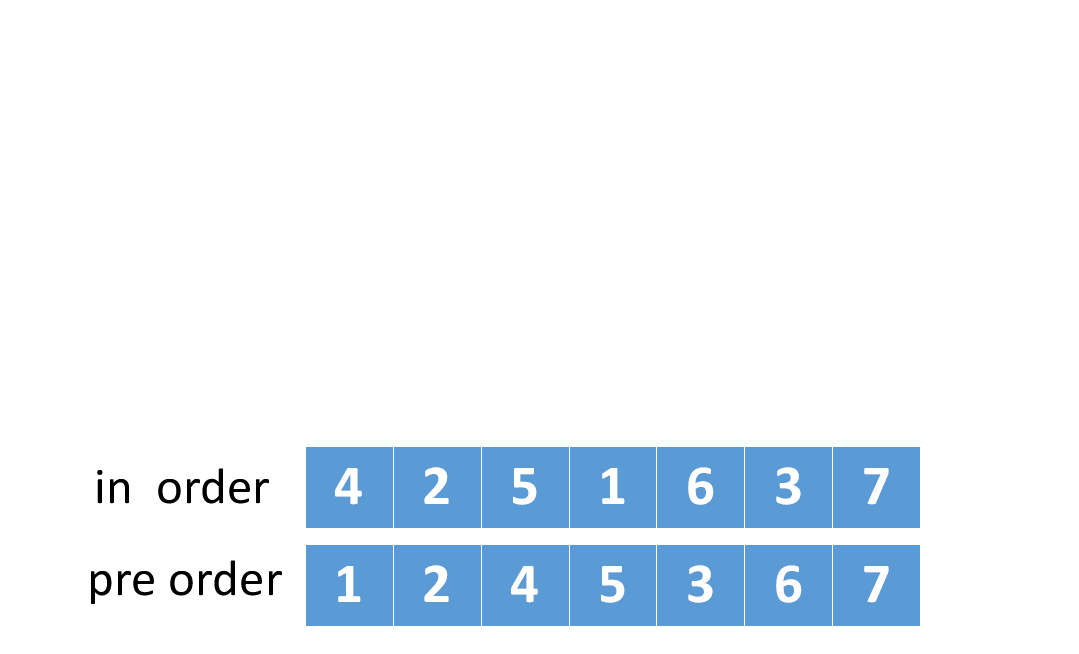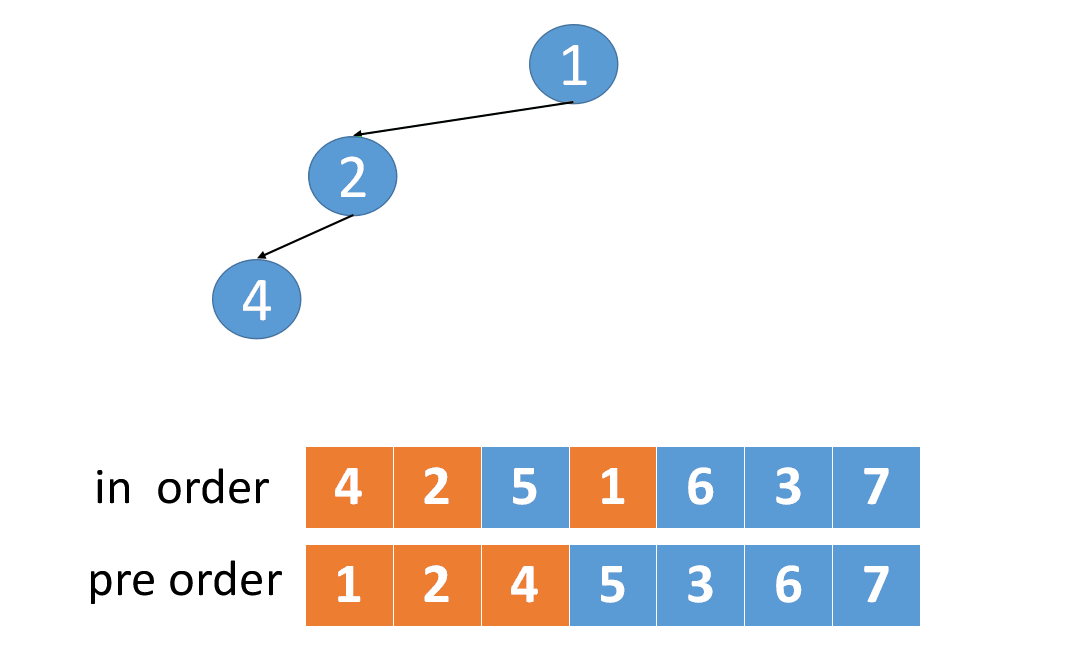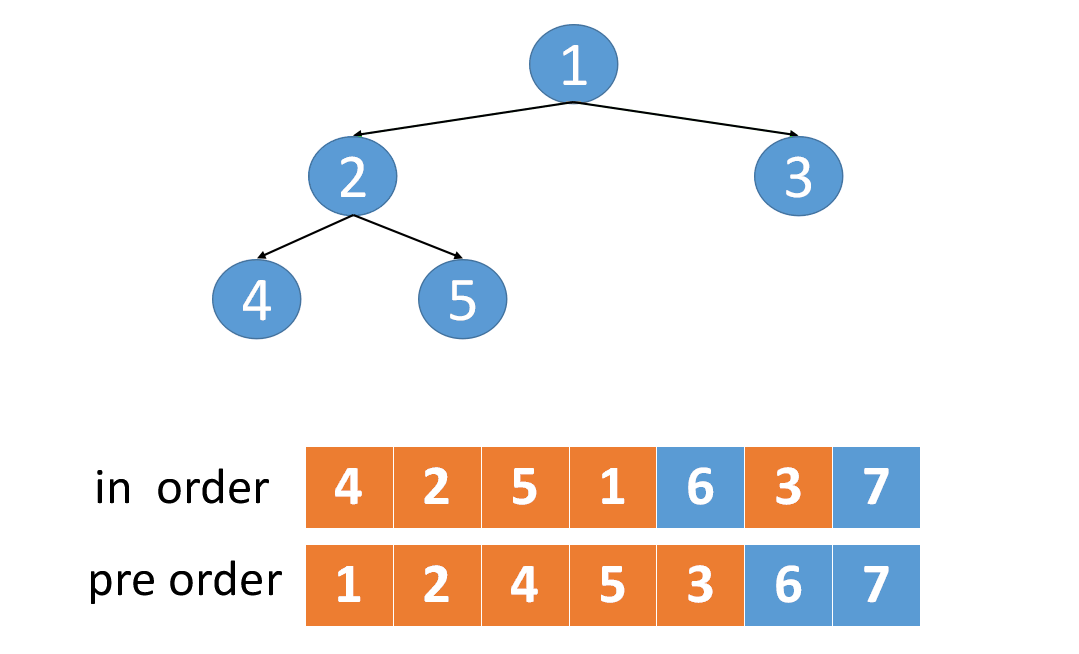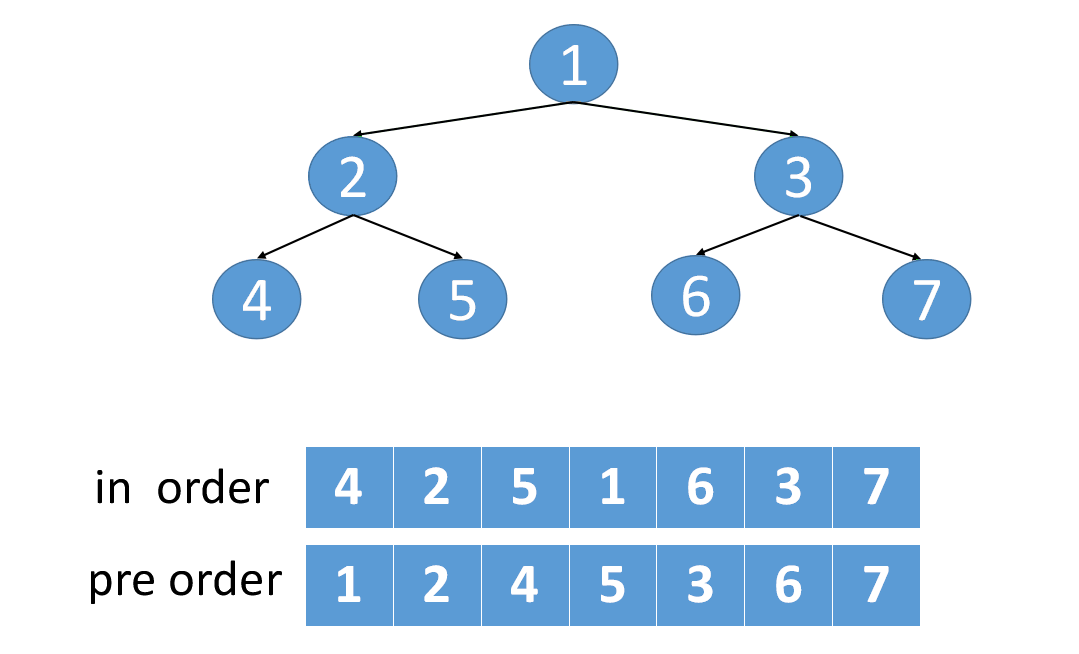
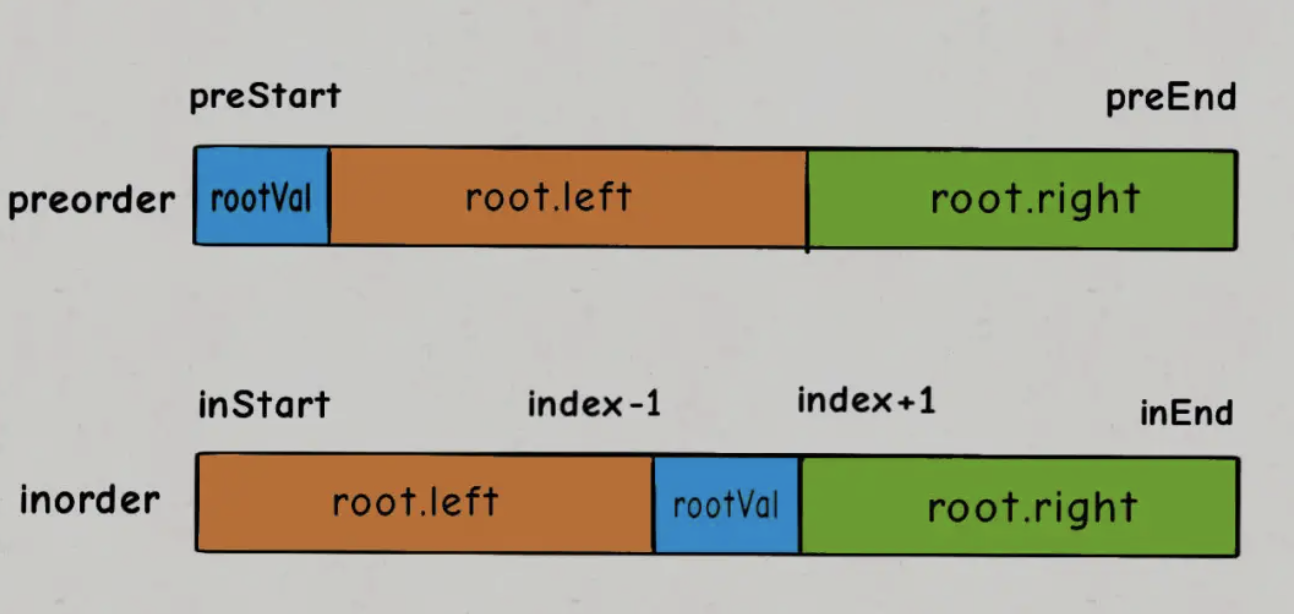
ListNode* preInTree2(int *pre,int *in,int n)  { n为当前二叉树的节点数if (n<=0)   return NULL;int i=0;while (in[i]!=pre[0])    此时i正好是左子树节点数。先序遍历的首元素一定是根节点i++;		在中序序列中找根ListNode* p=new ListNode;p->data=in[i];p->lc=preInTree2(pre+1,in,i);建左子树，从前序的pre+1开始对中序的0~i-1的左子序列的i个元素递归建立左子树p->rc=preInTree2(pre+i+1,in+i+1,n-i-1);		建右子树，从前序的pre+i+1开始对中序的i+1~n-1的右子序列的n-i-1个元素建立右子树return p;
}

(中in+后post)代码

ListNode* postInTree(int post[],int in[],int n)  {if (n<=0)   return NULL;int i=0;while (post[n-1]!=in[i])    此时i正好是左子树节点数。后序遍历的最后一个元素一定是根节点i++;	//i也正好是左子树节点数ListNode* p=new ListNode;p->data=in[i];p->lc=postInTree(post,in,i);		建左子树，从后序的post开始对中序的0~i-1的左子序列的i个元素递归建立左子树p->rc=postInTree(post+i,in+i+1,n-i-1);		建右子树，从前序的post+i开始对中序的i+1~n-1的右子序列的n-i-1个元素建立右子树return p;
}

只根据一种序列进行建树

只根据前序遍历建树

//课本202页
void BinaryTree::CreateBinTree(ifstream& in , BinTreeNode * & root)
{T data;if(!in.eof()){in>>data;if(data!='#'){root = new BinTreeNode(data);    //建立根节点if(root == NULL){cerr<<"存储分配错误！"<left);    //建立左子树CreateBinTree(in , root->right);    //建立右子树}elseroot=NULL;}
}

只根据中序遍历建树

BinTreeNode *BinaryTree::createTree(){char ch;
BinTreeNode *q,*current;
cin>>ch;
if(ch=='.')return NULL;//建立空树
else{q=creatTree();//建立左子树current=new BinTreeNode;current->data=ch;current->left=q;current->right=createTree();return current;}}

只根据后序遍历建树

BinTreeNode *BinaryTree::createTree(){char ch;
BinTreeNode *tl,*tr,*current;
cin>>ch;
if(ch=='.')return NULL;//建立空树
else{tl=creatTree();tr=creatTree();current=new BinTreeNode;current->data=ch;current->left=tl;current->right=tr;return current;}}

一棵具有n个节点的完全二叉树存放在二叉树的顺序存储结构中，试编写非递归算法对树的顺序存储结构转换为二叉链式存储结构

其实只要搞懂顺序存储结构二叉树的存储节点的方式，（当头节点为i时，则该节点的左孩子下标为2i，右孩子为2i+1）；

//将二叉树的顺序存储结构转换成二叉链存储结构
#include "btree.cpp"
#define MaxSize 30
typedef char Elemtype;
typedef ElemType SqBTree[MaxSize];
BTNode *trans(SqBTree a,int i)
{BTNode *b;if (i>MaxSize)return(NULL);if (a[i]=='#')	return  NULL;			//当节点不存在时返回NULLb=new BtNode;	//创建根节点b->data=a[i];b->lchild=trans(a,2*i);					//递归创建左子树b->rchild=trans(a,2*i+1);				//递归创建右子树return  b;								//返回根节点
}
int main()
{BTNode *b;SqBTree a;ElemType s[]="0ABCD#EF##G####################";b=trans(s,1);printf("b:");DispBTree(b);printf("\n");DestroyBTree(b);return 1;
}

n个结点的完全二叉树存放在二叉树的顺序存储结构中，编写非递归算法对该树进行中序遍历。

void Inorder(int  root， int n ，T trees[])//n个节点的完全二叉树，存储在数组trees中
{if（root == 0 ） return；stack s;while( root <=n || !s.empty() ){if(root <=n) //左子树入栈{s.push(root); root = root*2;}else {root = s.top(); visit (trees[root]);s.pop();root = root*2+1;    //转向右子树}}		}

实现一棵二叉树复制的算法。 

void copytree(treenode *from, treenode * & to )//拷贝from到to树,注意to参数为引用
{	if (from == NULL) {to = NULL; return;}to = new treenode ；to->data = from->data ; //1/拷贝根节点copytree(from->lchild,to->lchild);//2/拷贝左子树copytree(from->rchild,to->rchild)//3/拷贝右子树}

二叉树的所有叶子结点从左向右链接成单链表的算法 

void Creatlist(BinaryTreeNode*T,listNode*&L)//利用先序遍历递归，用链表L把结点串起来
{if (T != NULL) {if (T->left == NULL&&T->right == NULL) //如果左右子树为空，则为叶子结点{listNode *temp = new listNode;  //串起来temp->data = T->value;L->next = temp;L = L->next;    }Creatlist(T->left,L);     //递归左子树Creatlist(T->right,L);    //递归右子树}L->next = NULL;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！