信息论 卷积码

 前后码组有一定的相关关系

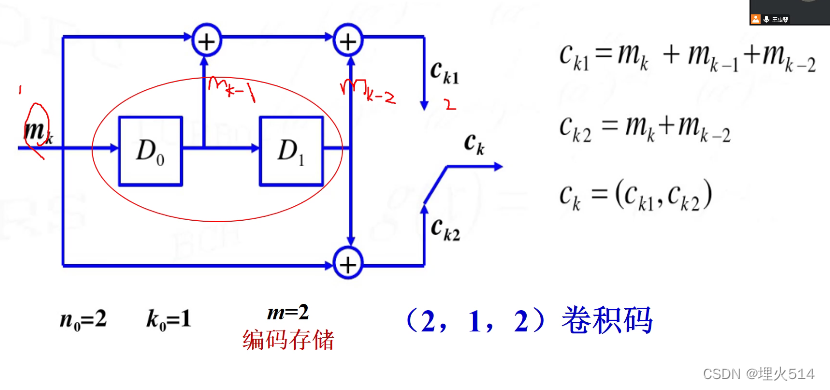
Di是移位寄存器，把给到的序列右移 

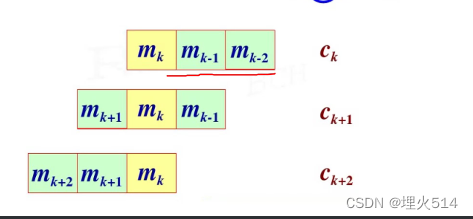
 第ck到第ck+2是受k影响，也就是，这三个码字之间有“约束度”

卷积码中各种符号的含义 

其中k为每次输入到卷积编码器的bit数，n为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度（移位寄存器的个数），也就是卷积编码器的k元组的级数，称m+1= K为编码约束度m称为约束长度

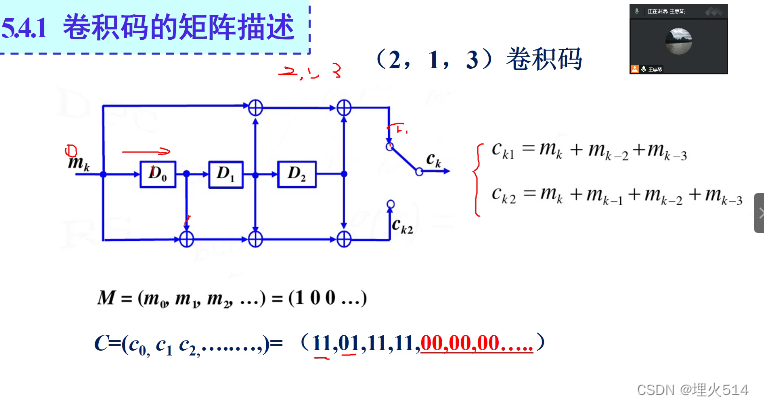
可以认为，是将1000.....逐渐右移再依次相加得到的

（这里C的异或结果出错了，正确的应该是11,10,01,01,00,11,00，.......） 

 用矩阵表示

这个矩阵就是把C的结果逐渐右移一个码元得到的，但是每次右移都有一个码元被吞掉，右边没有边界，全是0

它叫做基本生成矩阵

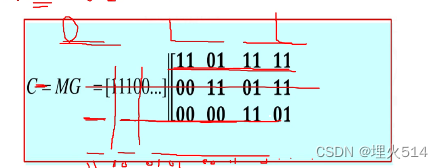
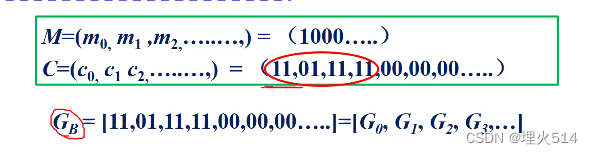
 取出G无穷中的第一行作为基本生成矩阵Gb

将Gb中直到最后一位非0元 的若干位拆分

D延迟一个码组就是右移两位 ，有点类似于伽罗瓦域乘法的x倍乘法，但后者是左移，D是右移

 ​​​​​​​​​​​​​​

 左下右上没写的全是0

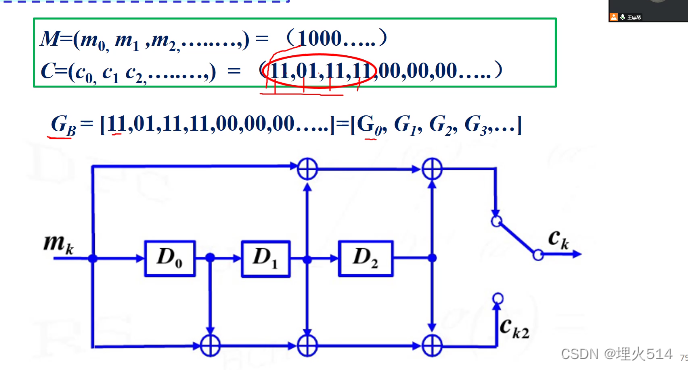
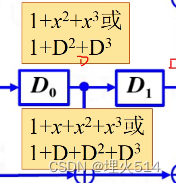
 一个D相当于x倍乘法里的x，但是是右移。然后用多项式表示移位情况

上面是CK1,下面是CK2

 ​​​​​​​

 ​​​​​​​​​​​​​​​​​​​​​

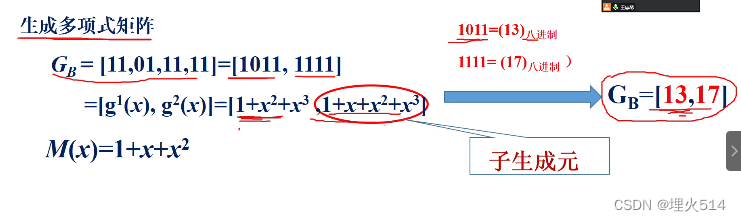
假设消息是1110 ，多项式表示就是1+x+x^2

 ​​​​​​​

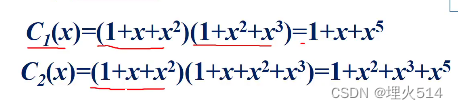
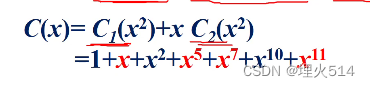
 C2比C1延迟一个单元，所以要乘x的1次幂

 卷积码状态转移图

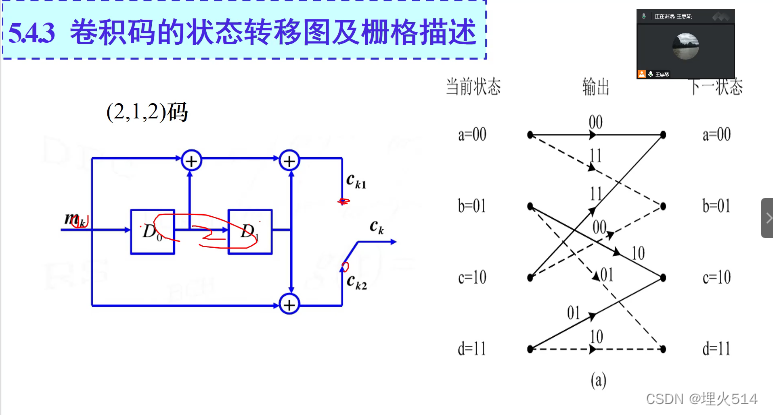
 实线 是输入了0码，虚线是1码

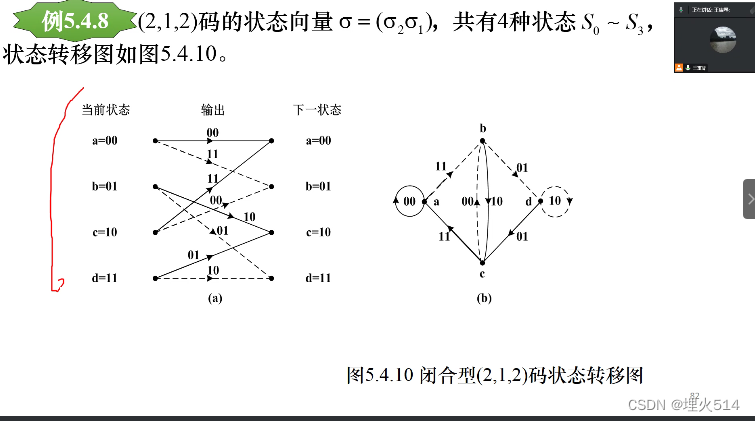
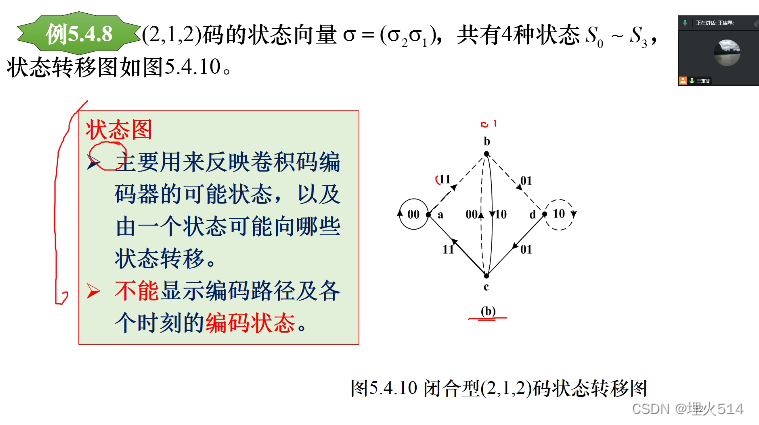
有效存储单

这里的虚线不表示输出0或1，仅仅标出了一条路径

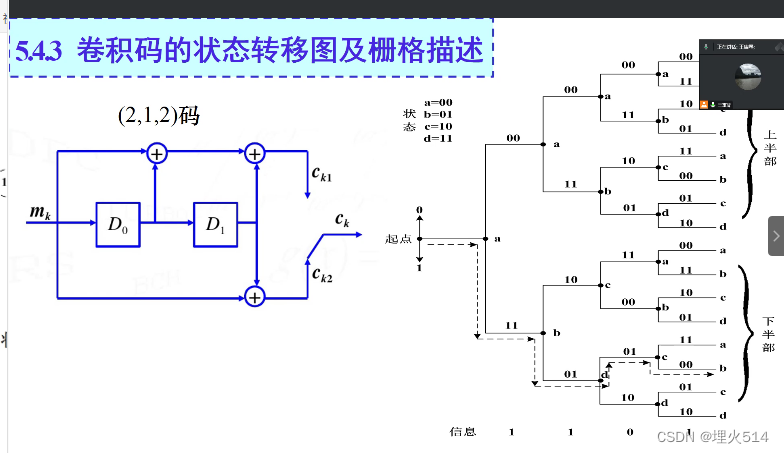
下面这个图里，一端虚线是1输入，一端实线是0，线段的数字代表对应的输出 

 用网格图表示的卷积码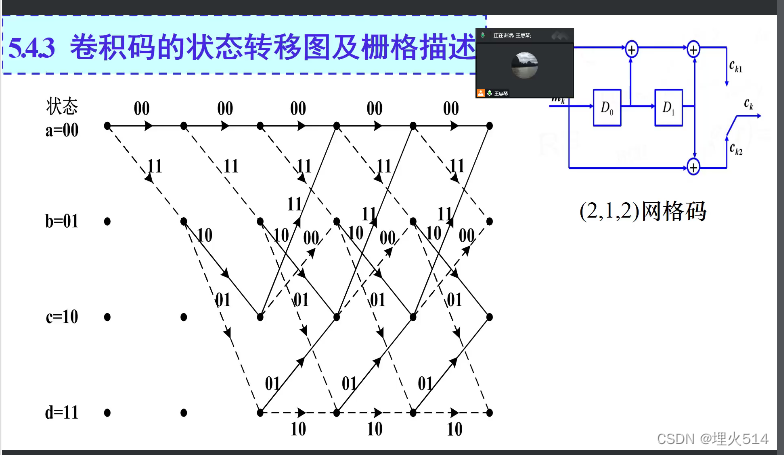

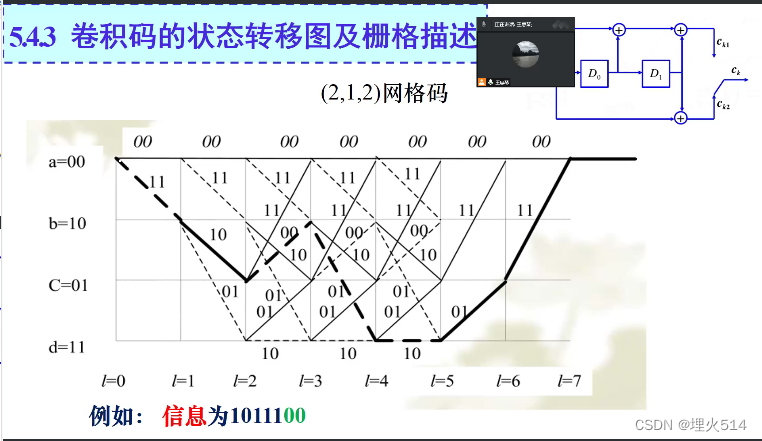
 加粗虚线表示了依次输入1011100时，状态的转移路径。最后两个0的作用是让寄存器置零0

卷积码译码方法 

 维特比译码算法

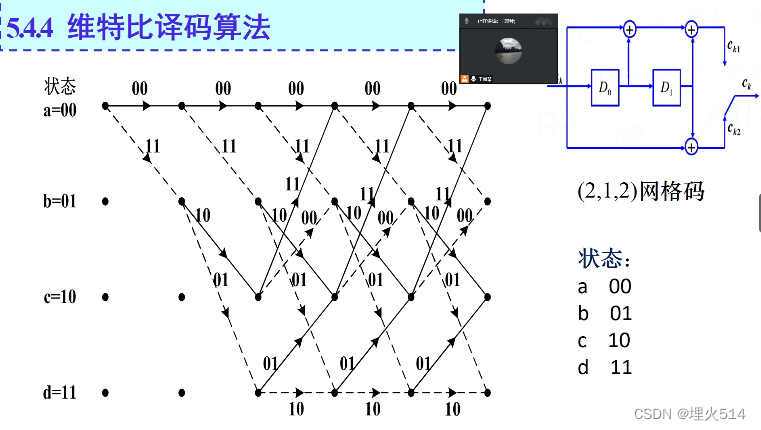
红色的表示码字出错

如何分段？

当前码是2,1,2,码，两个寄存器，两个输出 

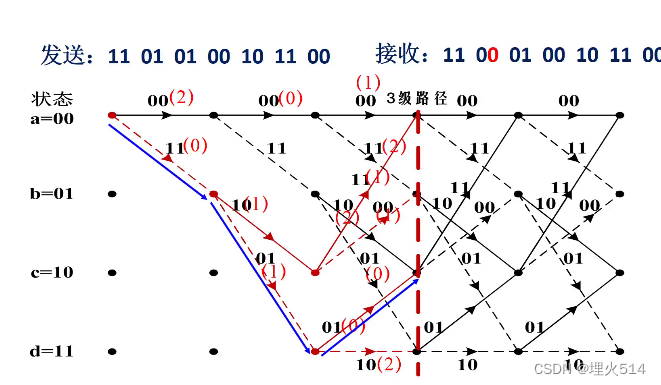
选出约束长度的编码，然后找出这个长度内各种可能的路径，并在路径中找出与收到编码汉明距离最小的，认为它是原本输入的编码

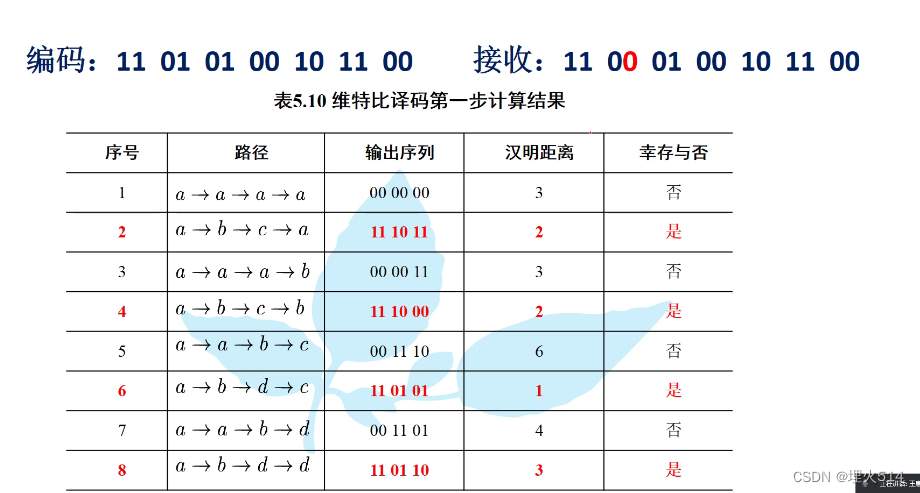
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！