OpenCV--040: OTSU二值寻找算法

Otsu最大类间方差法原则

利用阈值将原图像分成前景，背景两个图像。

该算法在灰度直方图的基础上采用最小二乘法原理推导出来的，具有统计意义上的最佳分割。

基本原理：
利用最佳阈值将图像的灰度值分割成两个部分，即背景与目标，使背景和目标之间的方差最大，具有最大的分离性。背景与目标之间的方差越大，说明构成图像的两个部分之间的差别越大，当部分目标被错分为背景或者部分背景被错分成目标，都会导致两部分之间的差别变小，当所取阈值的分割使类间方差最大时就意味着错分概率最小。

Otsu算法是一种自适应阈值确定的方法，计算简单，效率高，但对于光照不均的图像处理效果不是很好。

推导过程：

对一幅大小为M×N的数字图像：

令L表示灰度级数；

n i n_i ni​表示灰度级为$i$的像素数，图像中的像素总数 M N = n 1 + n 2 + n 3 + ⋅ ⋅ ⋅ + n L MN=n_1+n_2+n_3+···+n_L MN=n1​+n2​+n3​+⋅⋅⋅+nL​；

p i = n i / M N p_i=n_i/MN pi​=ni​/MN, p i p_i pi​为相对直方图，即灰度级为$i$出现的概率。则 ∑ i = 1 L p i = 1 \sum_{i=1}^{L}p_i=1 ∑i=1L​pi​=1;

设阈值$T(k)=k,1<k<L$可以将图像分成 C 1 C_1 C1​和 C 2 C_2 C2​两类，灰度值范围分别是[1,k]和[k+1,L]。

• 则被分成 C 1 C_1 C1​和 C 2 C_2 C2​的概率分别为：
  （ 1 ） ： P 1 ( k ) = ∑ i = 1 k p i （1）： P_1(k)=\sum_{i=1}^{k}p_i （1）：P1​(k)=i=1∑k​pi​
  （ 2 ） ： P 2 ( k ) = ∑ i = k + 1 L p i = 1 − P 1 ( k ) （2）：P_2(k)=\sum_{i=k+1}^{L}p_i=1-P_1(k) （2）：P2​(k)=i=k+1∑L​pi​=1−P1​(k)

• 则被分到 C 1 C_1 C1​和 C 2 C_2 C2​像素的灰度均值分别为：
  （ 3 ） ： m 1 ( k ) = ∑ i = 1 k i P ( i / C 1 ) = ∑ i = 1 k i P ( C 1 / i ) P ( i ) / P ( C 1 ) = 1 p 1 ( k ) ∑ i = 1 k i p i （3）：m_1(k)=\sum_{i=1}^{k}iP(i/C_1)=\sum_{i=1}^{k}iP(C_1/i)P(i)/P(C_1)=\frac{1}{p_1(k)}\sum_{i=1}^{k}ip_i （3）：m1​(k)=i=1∑k​iP(i/C1​)=i=1∑k​iP(C1​/i)P(i)/P(C1​)=p1​(k)1​i=1∑k​ipi​
  （ 4 ） ： m 2 ( k ) = ∑ i = k + 1 L i P ( i / C 2 ) = 1 p 2 ( k ) ∑ i = k + 1 L i p i （4）：m_2(k)=\sum_{i=k+1}^{L}iP(i/C_2)=\frac{1}{p_2(k)}\sum_{i=k+1}^{L}ip_i （4）：m2​(k)=i=k+1∑L​iP(i/C2​)=p2​(k)1​i=k+1∑L​ipi​

• 直至$k$级的累加均值：
  （ 5 ） ： m ( k ) = ∑ i = 1 k i p i （5）：m(k)=\sum_{i=1}^{k}ip_i （5）：m(k)=i=1∑k​ipi​

• 图像的灰度均值(即全局均值）：
  （ 6 ） ： m G = ∑ i = 1 L i p i （6）：m_G=\sum_{i=1}{L}ip_i （6）：mG​=i=1∑​Lipi​

由（3）和（4）得：
（ 7 ） ： P 1 m 1 + P 2 m 2 = m G （7）：P_1m_1+P_2m_2=m_G （7）：P1​m1​+P2​m2​=mG​
类间方差：
（ 8 ） ： σ B 2 = P 1 ( m 1 − m G ) 2 + P 2 ( m 2 − m G ) 2 （8）：σ_B^2=P_1(m_1-m_G)^2+P_2(m_2-m_G)^2 （8）：σB2​=P1​(m1​−mG​)2+P2​(m2​−mG​)2

将（7）中的 m G m_G mG​代入（8）中，以及由 P 1 + P 2 = 1 P_1+P_2=1 P1​+P2​=1得：
（ 9 ） ： σ B 2 = P 1 P 2 ( m 1 − m 2 ) 2 （9）：σ^2_B=P_1P_2(m_1−m_2)^2 （9）：σB2​=P1​P2​(m1​−m2​)2

最后由(3)(5)得 m 1 = 1 P 1 m m_1=\frac{1}{P_1}m m1​=P1​1​m，由（7）得 m 2 = m G − P 1 m P 2 m_2=\frac{m_G−P_1m}{P_2} m2​=P2​mG​−P1​m​,以及由 P 1 + P 2 = 1 P_1+P_2=1 P1​+P2​=1得：
σ B 2 = ( m G P 1 − m ) 2 P 1 ( P 1 − 1 ) σ^2_B=\frac{(m_GP_1−m)^2}{P_1(P_1−1)} σB2​=P1​(P1​−1)(mG​P1​−m)2​

所以要获取类间方差，只需要计算全局均值 m G 、 k m_G、k mG​、k级的累加均值$m$和累加概率 P 1 P_1 P1​。

设 σ G 2 σ^2_G σG2​代表全局方差，$\eta$表示可分性度量，表示可分割性：
σ G 2 = ∑ i = 1 L ( i − m G ) 2 p i σ^2_G=∑_{i=1}^{L}(i−m_G)^2p_i σG2​=i=1∑L​(i−mG​)2pi​
η = σ B 2 σ G 2 η=\frac{σ^2_B}{σ^2_G} η=σG2​σB2​​

最终的要计算的是：

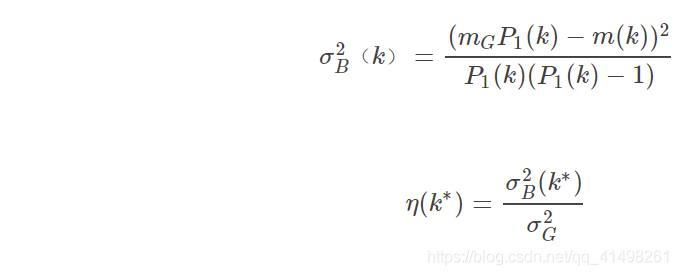
k ∗ k^∗ k∗是最佳阈值，即 σ B 2 ( k ) σ^2_B(k) σB2​(k)为最大值的k值。

算法基本步骤

1. 计算输入图像的相对直方图：根据 p i = n i / M N p_i=n_i/MN pi​=ni​/MN;
2. 计算像素被分到 C 1 C_1 C1​累计和 P 1 ( k ) P_1(k) P1​(k),根据上式(1)；
3. 计算累计均值m(k),根据上式（5）；
4. 计算全局灰度均值 m G m_G mG​,根据上式（6）；
5. 计算类间方差 σ B 2 ( k ) σ^2_B(k) σB2​(k),根据上式（10）；
6. 获取最大的 σ B 2 ( k ) σ^2_B(k) σB2​(k)中的k值，即为最佳阈值。
7. 计算可分性度量 η ∗ η^∗ η∗，根据上式(11) 。

• Matlab实现：

close all;
clear all;
clc;input = imread('R.png');%读图
input = rgb2gray(input);%灰度转换L = 256;%给定灰度级
[ni, li] = imhist(input,L);  %ni-各灰度等级出现的次数；li-对应的各灰度等级
% figure,plot(xi,ni);%显示绝对直方图统计
% title('绝对直方图统计')[M,N] = size(input);%获取图像大小
MN = M*N;%像素点总数%%Step1 计算归一化直方图pi = ni/MN;  %pi-统计各灰度级出现的概率
figure,plot(li,pi);%显示相对直方图统计
title('相对直方图统计')%%Step2  计算像素被分到C1中的概率P1(k)sum = 0;%用来存储各灰度级概率和
P1 = zeros(L,1);%用来存储累积概率和
for k = 1:Lsum = sum +pi(k,1);P1(k,1) = sum;%累加概率
end%%Step3  计算像素至K级的累积均值m(k)sum1 = 0;%用来存储灰度均值
m = zeros(L,1);%用来存储累计均值
for k = 1:Lsum1 = sum1+k*pi(k,1);m(k,1) = sum1;%累积均值
end%%Step4  计算全局灰度均值mgmg = sum1;%%Step5 计算类间方差sigmaB2 
sigmaB2 = zeros(L,1);
for k = 1:Lif(P1(k,1) == 0)sigmaB2(k,1) = 0;  %为了防止出现NaNelsesigmaB2(k,1) = ((mg*P1(k,1)-m(k,1))^2)/(P1(k,1)*(1-P1(k,1)));end
end%%Step6 得到最大类间方差以及阈值[MsigmaB2,T] = max(sigmaB2);%获取最大类间方差MsigmaB2，以及所在位置（即阈值）
output = zeros(M,N);%定义二值化输出图像
for i = 1:Mfor j = 1:Nif input(i,j)>Toutput(i,j) = 1;elseoutput(i,j)=0;endend
end
figure,imshow(output);%显示结果%%Step7 可分性度量etasigmaG2 = 0;%全局方差
for k = 1:LsigmaG2 = sigmaG2+(k-mg)^2*pi(k,1);
end
eta = MsigmaB2/sigmaG2;

int main() {Mat src = imread("D:/test/src.jpg",0);int row = src.rows;int col = src.cols;//图像的像素个数int MN = row * col;int thresh = 0;//统计直方图,求每个灰度值的总数Mat calchist;//统计图片的个数int nimages = 1;//通道数量int channels[1] = { 0 };//输出直方图int histSize[1] = { 256 };//每一维数值的取值范围rangesfloat hranges[2] = { 0,255 };//每一维数值的取值范围const float* ranges[1] = { hranges };calcHist(&src, nimages, channels, Mat(), calchist, 1, histSize, ranges);cout << calchist.rows << "  " << calchist.cols << endl;//计算每个像素在整幅图像中的比例float pi[256];for (int i = 0; i < calchist.rows; i++) {for (int j = 0; j <calchist.cols ; j++){pi[i] = (float)calchist.at<int>(i,j) / (float)MN;}}//经典ostu算法,得到前景和背景的分割//遍历灰度级[0,255],计算出方差最大的灰度值,为最佳阈值float w0, w1, u0tmp, u1tmp, u0, u1, u, deltaTmp, deltaMax = 0;for (int i = 0; i < 256; i++) {w0 = w1 = u0tmp=u1tmp=u0=u1=u=deltaTmp=0;for (int j = 0; j < 256; j++) {if (j <= i) {//背景部分//以i为阈值分类，第一类总的概率w0 += pi[i];u0tmp += j * pi[j];}else {  //前景部分//以i为阈值分类，第二类总的概率w1 += pi[i];u1tmp += j * pi[j];}}u0 = u0tmp / w0;//第一类的平均灰度u1 = u1tmp / w1;//第二类的平均灰度u = u0tmp + u1tmp;//整幅图像的平均灰度//计算类间方差：deltaTmp = w0 * (u0 - u) * (u0 - u) + w1 * (u1 - u) * (u1 - u);//找到最大类间方差以及对应的阈值if (deltaTmp > deltaMax) {deltaMax = deltaTmp;thresh = i;}}/*ThresholdTypes:THRESH_BINARY     = 0, //!< \f[\texttt{dst} (x,y) =  \fork{\texttt{maxval}}{if \(\texttt{src}(x,y) > \texttt{thresh}\)}{0}{otherwise}\f]THRESH_BINARY_INV = 1, //!< \f[\texttt{dst} (x,y) =  \fork{0}{if \(\texttt{src}(x,y) > \texttt{thresh}\)}{\texttt{maxval}}{otherwise}\f]THRESH_TRUNC      = 2, //!< \f[\texttt{dst} (x,y) =  \fork{\texttt{threshold}}{if \(\texttt{src}(x,y) > \texttt{thresh}\)}{\texttt{src}(x,y)}{otherwise}\f]THRESH_TOZERO     = 3, //!< \f[\texttt{dst} (x,y) =  \fork{\texttt{src}(x,y)}{if \(\texttt{src}(x,y) > \texttt{thresh}\)}{0}{otherwise}\f]THRESH_TOZERO_INV = 4, //!< \f[\texttt{dst} (x,y) =  \fork{0}{if \(\texttt{src}(x,y) > \texttt{thresh}\)}{\texttt{src}(x,y)}{otherwise}\f]*/Mat dst;threshold(src, dst, thresh, 255, 0);imshow("dst", dst);imshow("src", src);waitKey(0);return 0;}

OpenCV中自带OTSU

THRESH_OTSU和前面的type可以组合使用，好处是不用自己指定thresh值，系统会进行计算并且作为返回值返回。

THRESH_OTSU文档上说如果图像黑白分明，就可以用这个，我试了一下，用扫描仪扫描的一个带文字的图像，由于没有光照的差异，算是黑白分明的了，用这个参数得到的结果和自己多次调整thresh得到的最优结果几乎是一样的。

Mat src = imread("D:/test/src.jpg", 0);Mat dst;threshold(src, dst, 0, 255, THRESH_BINARY | THRESH_OTSU);imshow("src", src);imshow("dst", dst);waitKey(0);

学习：
OTSU算法对图像二值化
算法解剖系列-Otsu二值化原理及实现

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！