数字调制解调——QAM调制

QAM调制（Quadrature Amplitude Modulation，正交振幅调制）是一种数字调制技术，通过调整调制信号的振幅和相位来携带数字信息。它基于两个正交的调制信号（I信号和Q信号），将数字信息转换为调制信号的振幅和相位。

通俗来讲，在信号中，所谓的正交是指两个两个信号相差90°，那么在QAM中即存在相位的调制，也是存在着振幅的调制。

QAM调制的原理可以分为两个主要步骤：符号映射和载波调制。

符号映射：
在符号映射阶段，数字信息被分成多个符号，每个符号代表一个特定的振幅和相位组合。常见的QAM调制包括16-QAM、64-QAM和256-QAM等，它们分别使用16、64和256个不同的符号来表示数字信息。

QAM调制将数字信息映射到不同的调制符号，其中M表示QAM调制的阶数（符号数），通常为2的幂次方。

举个例子来具体说明一下吧，对于一个2bit的数，它每一个bit位数有两种情况（0，1），也就是说这个2bit 的数可以是00、01、10、11四种情况，那么这四种情况代表了4bit的信息，推导一下，4bit的数所包含的信息是2^4
个，对于Mbit的数呢，它所包含的信息是2^M个，所以比特位越多，所能传输的信息量就越大。回到我们的QAM调制中，数字16表示调制的阶数或调制符号的数量。
每个二进制位可以表示2个不同的状态（0或1），因此4位二进制可以表示2^4 = 16个不同的组合。这样，每个4位二进制序列可以对应一个唯一的调制符号。也就是需要一组4位的二进制数来表示。 所以从理论上来说，m-QAM中的m越大，所能传输的信息量就越大，传输速率也就越快。

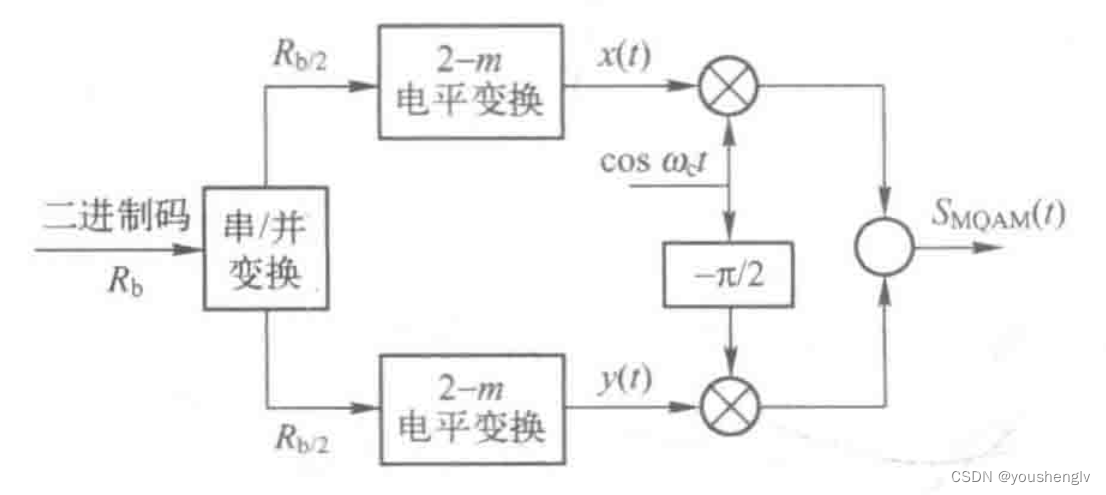
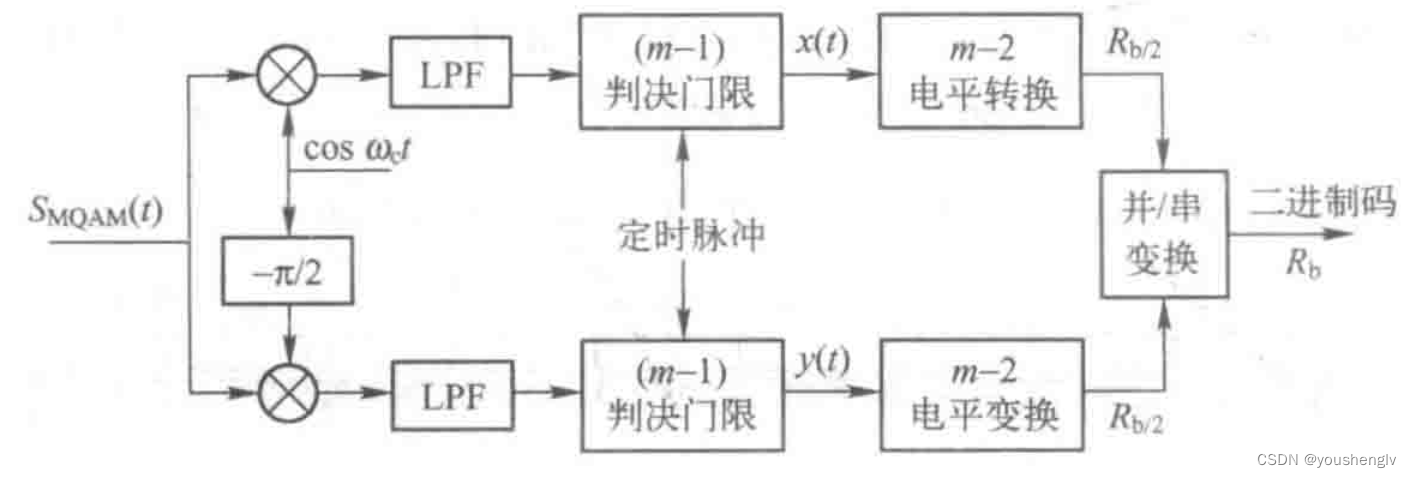
接下来给出16-QAM调制的MATLAB代码：

%%%%%**** 16-QAM调制   ****%%%%%
%%%%%**** data:20230626   ****%%%%%clear all;
clc;
close all;N=1000;    %设定码元数量
fb=1;      %基带信号频率
fs=16;     %抽样频率
fc=4;      %载波频率，为便于观察已调信号，把载波频率设得较低msg=randi([0 1],1,N);   %产生二进制信号序列%%%%%%%%串并转换%%%%%%%%
I_bit = msg(1:2:length(msg));    %% N/2 个比特
Q_bit = msg(2:2:length(msg));    %% N/2 个比特T=[0 1;3 2];
for i=1:2:length(I_bit)I_bit2=I_bit(i:i+1)+1;ISymbol((i+1)/2)=T(I_bit2(1),I_bit2(2))-1.5;Q_bit2=Q_bit(i:i+1)+1;QSymbol((i+1)/2)=T(Q_bit2(1),Q_bit2(2))-1.5;   
endfigure(1);
subplot(2,1,1);
stem(ISymbol);title('I路符号');
subplot(2,1,2);
stem(QSymbol);title('Q路符号');%对基带信号进行16QAM调制，fb=1;I路和Q路的符号速率分别为1/4，而fs=32，因此
% 过采样率为32X4=128，所以最后产生的数据有N/4X128个OverSamp=fs/(fb/4);     %过采样率=32/(1/2)=64
span=3;                %表示滚降系数的时间范围
alpha=0.5;              %滚降系统； B=1000/2*(1+0.5)=750Hz
h = rcosdesign(alpha,span,OverSamp,'sqrt');   %成型滤波器设计
ISymbol_OverSample= kron(ISymbol,[1 zeros(1,OverSamp-1)]);
QSymbol_OverSample= kron(QSymbol,[1 zeros(1,OverSamp-1)]);% ISymbol_OverSample=upsample(I_bit,32);
% QSymbol_OverSample=upsample(Q_bit,32);SendShape_I = filter(h,1,ISymbol_OverSample);   %I路滤波
SendShape_Q = filter(h,1,QSymbol_OverSample);   %Q路滤波figurefreqz(h);
subplot(2,1,1);
plot(SendShape_I); title('脉冲成型后的I路波形');
subplot(2,1,2);
plot(SendShape_Q); title('脉冲成型后的Q路波形');N=0:length(SendShape_I)-1;QamSignal=SendShape_I.*cos(2*pi*fc*N/fs)-SendShape_Q.*sin(2*pi*fc*N/fs);figure;
plot(abs(fft(QamSignal))); title('QAM信号的频谱');%%%%%%%%%%% 解调  %%%%%%%%%%%%
DemodeWave_I = QamSignal.*cos(2*pi*fc*N/fs);
DemodeWave_Q = QamSignal.*sin(2*pi*fc*N/fs);figure;
subplot(2,2,1);plot(DemodeWave_I);title('解调后的I路时域波形');
subplot(2,2,2);plot(abs(fft(DemodeWave_I)));title('解调后的I路频域波形');
subplot(2,2,3);plot(DemodeWave_Q);title('解调后的Q路时域波形');
subplot(2,2,4);plot(abs(fft(DemodeWave_Q)));title('解调后的Q路频域波形');%%%%%%%%%%  匹配滤波接收  %%%%%%%%%%%%
RcvMatch_I = filter(h,1,SendShape_I);
RcvMatch_Q = filter(h,1,SendShape_Q);figure;
subplot(2,1,1); plot(RcvMatch_I);
title('匹配滤波后的I路');
subplot(2,1,2); plot(RcvMatch_Q);
title('匹配滤波后的Q路');%%%%%%%%%%    抽样判决   %%%%%%%%%%%%
%%%% 符号抽样  %%%%
SymPosi=1:OverSamp:length(RcvMatch_I)-1;
RcvI=RcvMatch_I(SymPosi);
RcvQ=RcvMatch_Q(SymPosi);figure;
subplot(2,1,1);stem(RcvI);
title('I路抽样判决后的符号');
subplot(2,1,2);stem(RcvQ);
title('Q路抽样判决后的符号');%%%%%% 4电平到2比特的映射  %%%%%%
%%%先把 +-0.5，+-1.5转换为0，1，2，3.然后再转换为00，01，11，10%%%%
%%%映射规则：-1.5-->00；0.5-->10; 0.5-->11; -0.5-->10%%%I0=find(RcvI<-1);
YoutI(I0) = 0;
I1=find(-11);
YoutI(I3) = 2;Q0=find(RcvQ<-1);
YoutQ(Q0) = 0;
Q1=find(-11);
YoutQ(Q3) = 2;% 一位四进制码元转换为两位二进制码元
for i=1:length(msg)/4YoutIbit(2*i-1:2*i) = de2bi(YoutI(i),'left-msb',2);YoutQbit(2*i-1:2*i) = de2bi(YoutQ(i),'left-msb',2);
endYoutIQ = [YoutIbit;YoutQbit];
Yout = YoutIQ(:)';figure;
subplot(2,1,1);
plot(msg);title('原始信号时域图');
subplot(2,1,2);
plot(Yout);title('最终信号时域图');
errorbit = sum(abs(Yout-msg))

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！